Задача 4
Вычислить интегралы.
4.1.
1)
2)
4.2.
1)
2)
4.3.
1)
2)
4.4.
1)
2)
4.5.
1)
2)
4.6.
1)
2)
4.7.
1)
2)
4.8.
1)
2)
4.9.
1)
2)
4.10.
1)
2)
Задача 5
С помощью определенного интеграла найти площадь фигуры, ограниченной линиями.
5.1.
.
5.2.
5.3.
5.4.
5.5.
5.6.
5.7.
5.8.
5.9.
5.10.
Задача 6
Систему линейных алгебраических уравнений решить тремя способами:
1) методом Гаусса;
2) по формулам Крамера;
6.1.
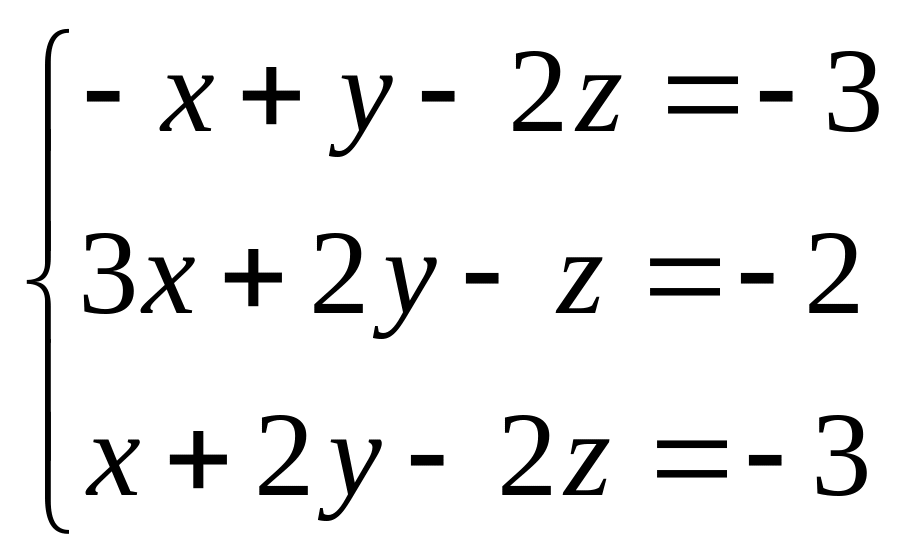
6.2.
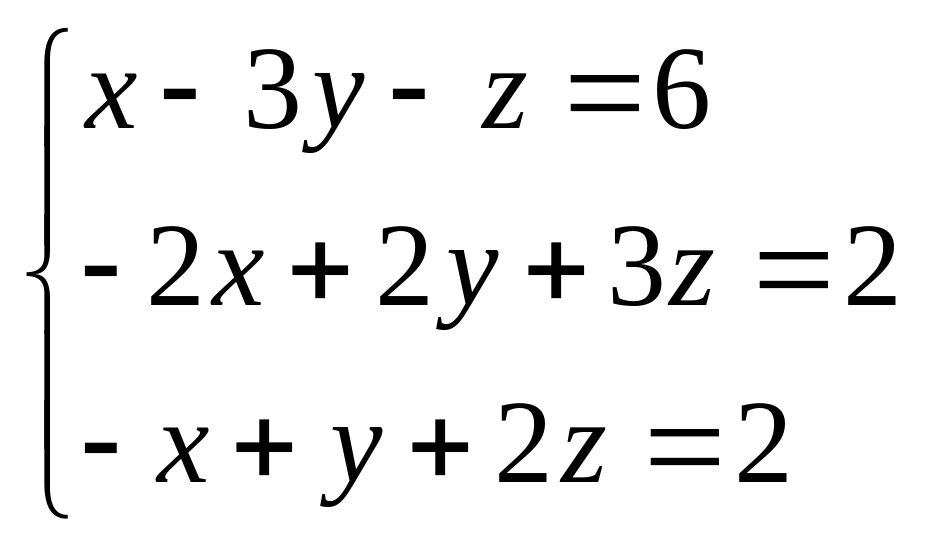
6.3.
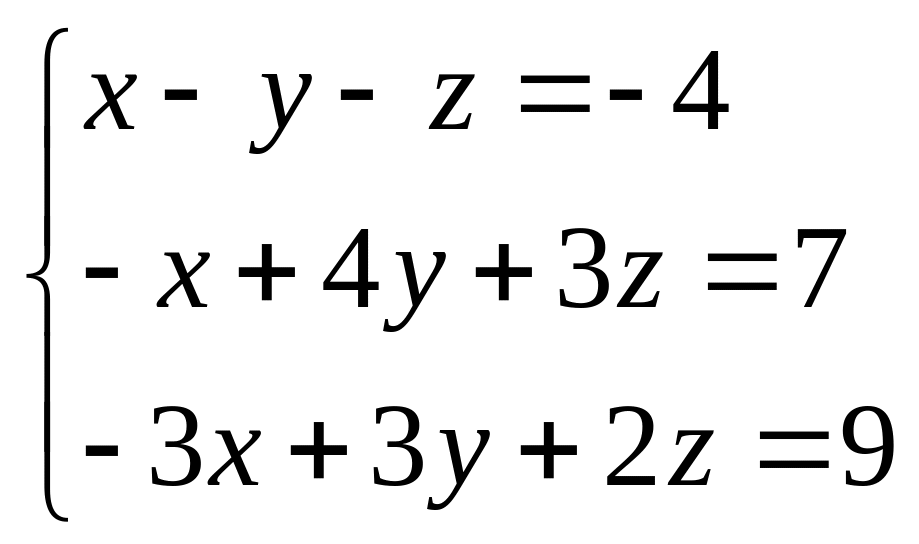
6.4.
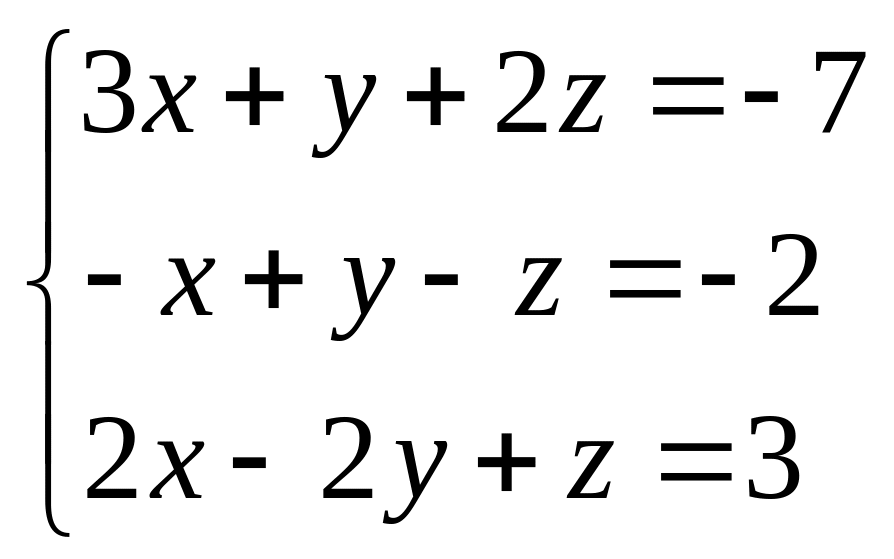
6.5.
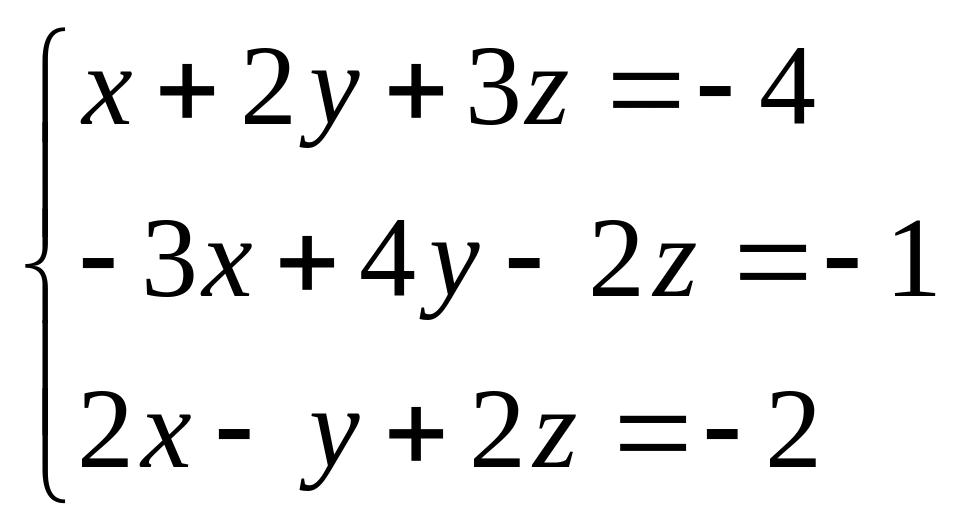
6.6.
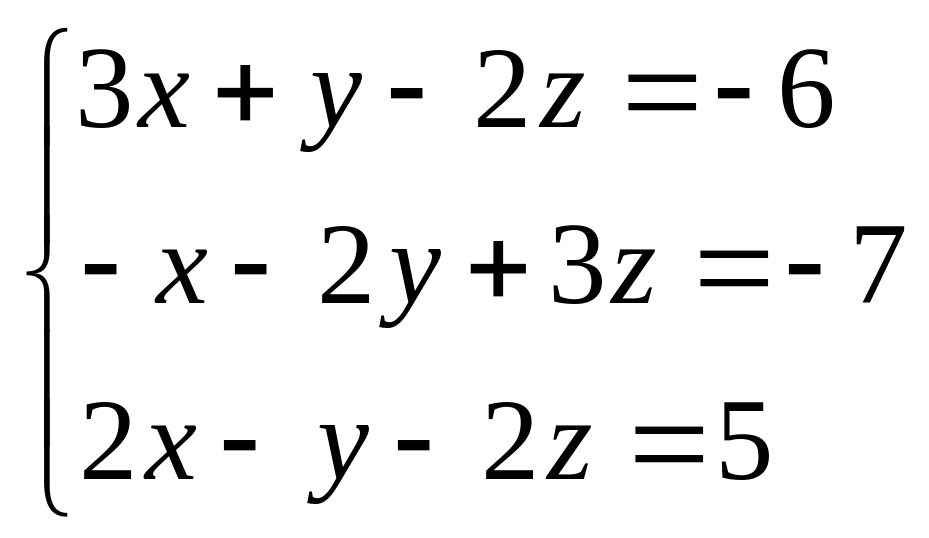
6.7.
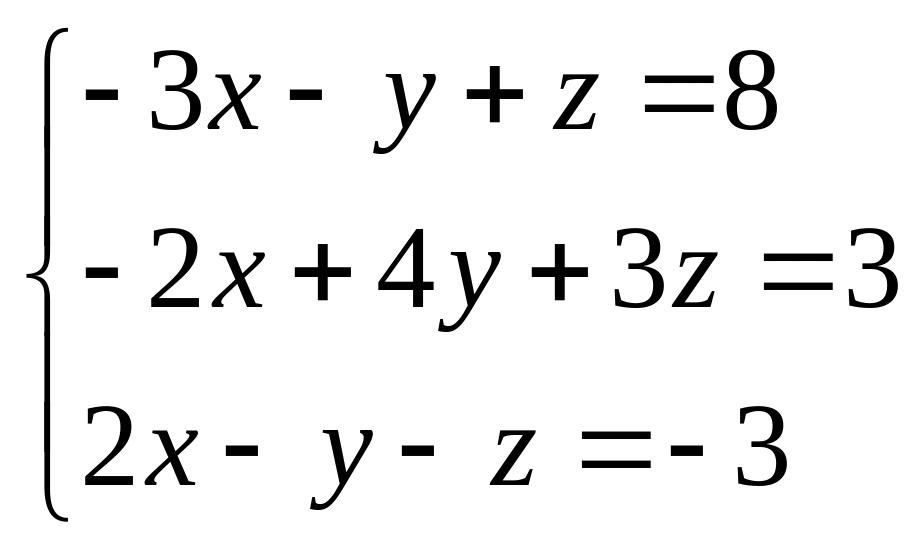
6.8.
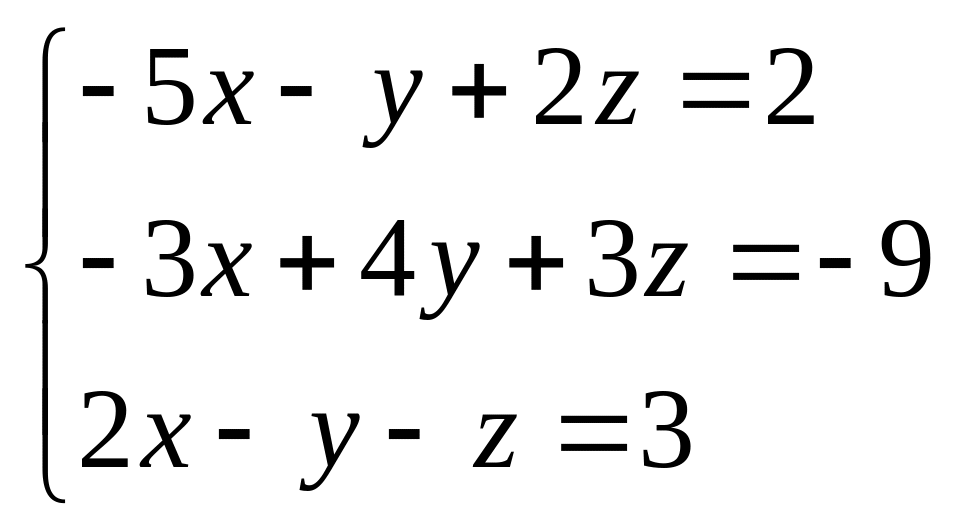
6.9.
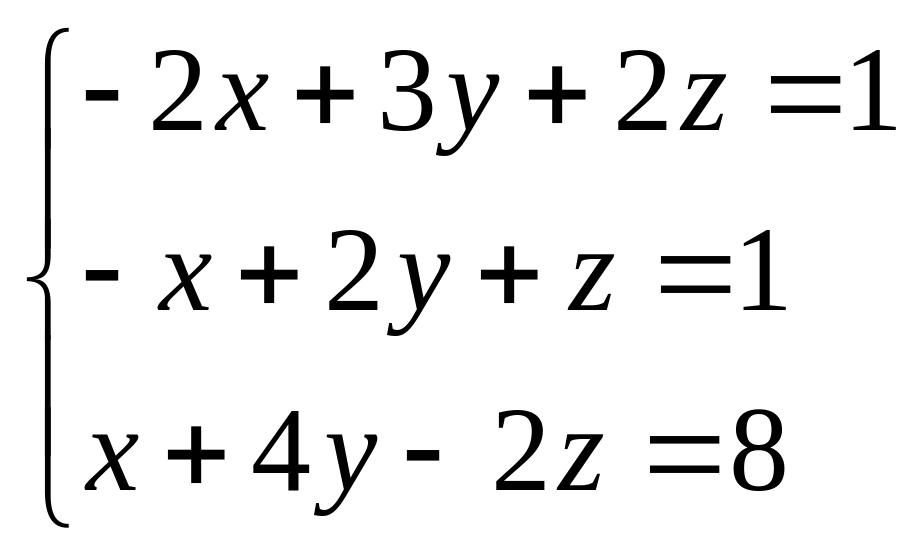
6.10.
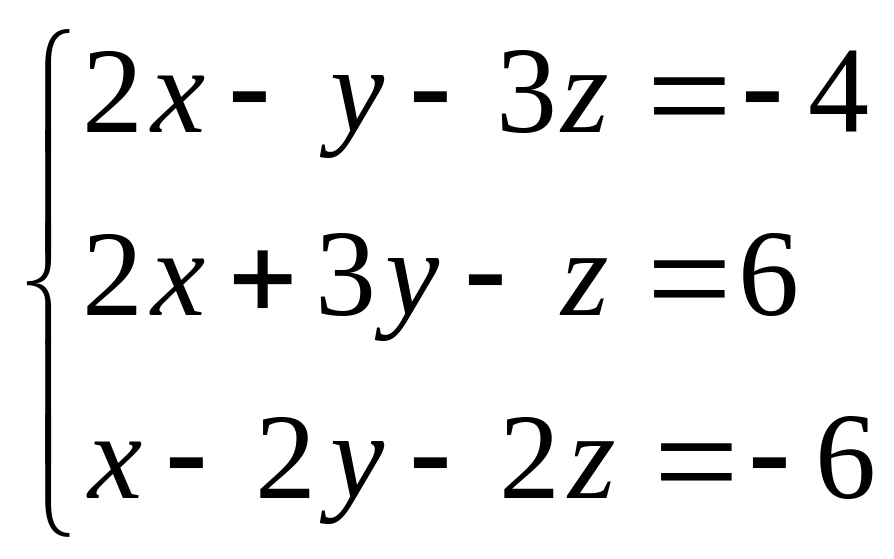
Вопросы к экзамену
Определение функции. Основные свойства функций.
Определение предела функции в точке
Бесконечно малые функции и их свойства. Бесконечно большие функции и их свойства. Правила сравнения бесконечно больших функций.
Арифметические свойства конечных пределов.
Непрерывность функции. Точки разрыва и их классификация.
Определение производной. Геометрический смысл производной.
Основные правила дифференцирования. Таблица производных.
Определение возрастающей и убывающей функций.
Определение экстремумов функции. Необходимое условие экстремума. Достаточное условие экстремума в терминах первой производной.
Направление выпуклости кривой. Необходимое условие выпуклости кривой. Достаточное условие выпуклости кривой.
Определение точки перегиба кривой. Необходимое условие точки перегиба. Достаточное условие точки перегиба.
Определение первообразной и неопределенного интеграла. Основные свойства неопределенных интегралов. Таблица интегралов.
Метод замены переменной в неопределенном интеграле
Определение определенного интеграла и его геометрический смысл.
Вычисление определенного интеграла по формуле Ньютона-Лейбница.
Геометрические приложения определенного интеграла: вычисление площадей, объемов.
Определение функции двух переменных. Предел и непрерывность.
Частные производные и их геометрический смысл.
Экстремум функции двух переменных.
Условный экстремум функции двух переменных.
Определители второго и третьего порядка. Свойства определителей. Вычисление определителей.
Матрицы и действия с ними. Определитель квадратной матрицы и его вычисление.
Обратная матрица и ее нахождение.
Решение матричных уравнений с помощью обратной матрицы.
Ранг матрицы. Вычисление ранга матрицы.
Системы линейных уравнений.
Правило Крамера решения системы линейных уравнений.
Решение систем линейных уравнений методом Гаусса.
Решение систем уравнений методом обратной матрицы.
Список рекомендуемых источников:
Основная литература (с грифом)
|
|
|
|
|
|
Дополнительная литература
|
|
|
|
|
|