8. Механическая у угловая характеристики синхрон-ногодвигателя

Угловая скорость синхронного двигателя при постоянстве частоты напряжения статора при работе в установившемся режиме при изменении момента от – М_МАХ до + М_МАХ остается строго постоянной и равна синхронной скорости

где f₁ – частота питающего статор напряжения, р – число пар полюсов.

Поэтому механическая характеристика синхронного двигателя – прямая линия, параллельная оси абсцисс. Если момент нагрузки превышает М_МАХ, то двигатель может выпасть из синхронизма и зависимость M = f() нарушится.

При пульсации нагрузки на валу двигателя в установившемся режиме значение мгновенной скорости колеблется около среднего значения. Эти колебания происходят за счет изменения угла между напряжением и ЭДС синхронной машины. Колебания скорости имеют практическое значение при работе синхронного двигателя на пульсирующую нагрузку, например на поршневой компрессор. Для решения вопроса об устойчивой работе двигателя в таких случаях необходимо знать зависимость момента М от угла между напряжением и ЭДС. Зависимость момента М синхронной машины от угла  носит название угловой характеристики. Этому углу соответствует пространственный угол сдвига между осью результирующего поля машины и осью полюсов (пространственный угол в р раз меньше угла ).

Для нахождения уравнения угловой характеристики обратимся к упрощенной векторной диаграмме неявнополюсной машины, представленной на рис. 3.40.

Если пренебречь потерями в активном сопротивлении статора, считая R₁ = 0 (рис. 3.40), то подводимая к синхронному двигателю мощность, Вт, может быть принята равной электромагнитной мощности:

(3.82)

где I и U – фазные ток и напряжение.

Из векторной диаграммы (рис. 3.40) следует, что

(3.83)

Из рассмотрения вспомогательного треугольника АВС видно, что

следовательно

(3.84)

Теперь, подставив полученное выражение в (3.82), получим уравнение электромагнитной мощности, Вт,

(3.85)

где I_КЗ – ток короткого замыкания, .

Отсюда электромагнитный момент

(3.86)

В случае явнополюсной машины появляется еще дополнительный реактивный момент. Однако для практических расчетов им можно пренебречь и пользоваться формулой (3.86).При  = 90° момент имеет максимальное значение:

(3.87)

Поэтому искомое уравнение угловой характеристики принимает следующий вид:

(3.88)

С увеличением нагрузки угол возрастает. Из (3.88) видно, что вначале с увеличением угла растет и развиваемый двигателем момент (рис. 3.42), что удовлетворяет требованию устойчивой работы двигателя. В правой части графика при > 90° условие устойчивой работы двигателя нарушается, так как при увеличении нагрузки уголпродолжает возрастать, а момент, развиваемый двигателем, уменьшается, вследствие чего двигатель выпадает из синхронизма. Левая часть характеристики является рабочей частью, а правая, где угол изменяется от 90 до 180°, представляет собой неустойчивую часть характеристики

Номинальному моменту двигателя М_НОМ практически соответствует угол  = 25 – 30°. При этом кратность, максимального момента к номинальному составляет:

.

Однако в специальных случаях применяют синхронные машины и с большей кратностью максимального момента, достигающей 3,5 – 4.

Синхронный двигатель может работать и в режиме генератора параллельно с сетью при синхронной угловой скорости, когда нагрузочный момент на его валу будет иметь отрицательное значение. Для торможения такой режим практического значения не имеет, так как при этом нельзя получить снижения скорости.

Обычно применяется динамическое торможение синхронных двигателей, при котором обмотки статора отключаются от сети и замыкаются на резисторы (рис. 3.43). Механические характеристики в этом случае подобны характеристикам асинхронного двигателя при динамическом торможении. Интенсивность торможения зависит от сопротивления статорной цепи и от потока, создаваемого током роторной обмотки. Время торможения при питании цепей возбуждения от собственного возбудителя, находящегося на валу синхронного двигателя, больше, чем при питании от независимого источника постоянного тока. Объясняется это тем, что при снижении угловой скорости возбудителя уменьшается его ЭДС, а, следовательно, уменьшаются ток возбуждения двигателя и тормозной момент.

Торможение синхронных двигателей противовключением практически не применяется, так как оно сопровождается большими толчками тока и ведет к усложнению управления ввиду необходимости отключения двигателя при подходе к нулевой скорости.

Управление механической характеристикой СД осуществляется только изменением частоты питающего статор напряжения. При этом так как изменяется Х₁ необходимо изменять величину напряжения или ток возбуждения ротора.

ГЛАВА ЧЕТВЕРТАЯ

ПУСК И ТОРМОЖЕНИЕ ЭЛЕКТРОПРИВОДА

ПУСК И ТОРМОЖЕНИЕ ЭЛЕКТРОПРИВОДА С ДВИГАТЕЛЕМ ПОСТОЯННОГО ТОКА НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ.

Пуск двигателя постоянного тока с независимым возбуждением можно осуществить путем регулируемого увеличения напряжения на якоре, изменении сопротивления в цепи якоря. При увеличении напряжения на якоре можно получить любую оптимальную диаграмму пуска электромеханической системы. Затраты энергии без учета потерь для пуска электромеханической системы оптимальной по быстродействию (М = const)

(4.1)

Переменные потери энергии при пуске в этом случае

(4.2)

где R_Я – суммарное сопротивление якорной цепи двигателя.

Так как i_Я при постоянном возбуждении пропорционален моменту двигателя, то

(4.3)

Время пуска рассчитывается, как было рассмотрено в разделах 1.6 и 1.7. Кривая (t) определяется дифференцированием основного уравнения движения. При диаграмме (t), обеспечивающей минимум мощности двигателя (см. раздел 1.8) момент двигателя изменяется по закону

Затраты энергии рассчитываются по формуле 4.1, а потери энергии будут равны

(4.4)

Время пуска и график (t) определяется также как и в предыдущем случае.

При пуске путем изменения сопротивления в цепи якоря при дискретном его изменении реализация оптимальной диаграммы практически невозможна.

На практике пуск осуществляют при изменении момента двигателя от некоторого значения М₁ до М₂. Величина М = М₁ – М₂ зависит от числа ступеней и с увеличением числа ступеней уменьшается. В пределе при числе ступеней пуска стремящемся к , можно реализовать пуск при постоянном моменте. Как правило число ступеней лежит в интервале от 2 до 10.

Диаграмма изменения момента и скоростей при переключении сопротивлений показана на рис. 4.1. На рисунке М₁ и М₂ – моменты двигателя, при которых происходит переключение сопротивлений;1 – естественная характеристика; 2 – первая пусковая характеристика; 3,4 – вторая и третья первая пусковые характеристики; М_С – момент сопротивления электромеханической системы.

Пуск осуществляется следующим образом. При подаче напряжения на двигатель изменение  и М происходит по линии 2. Когда скорость увеличится до значения , часть сопротивления шунтируется коммутационным аппаратом и пуск продолжается по линии 3, затем по линии 4, до значения  = ₃ и затем по естественной характеристике 1 до установившегося значения скорости.

В настоящее время пуск двигателя постоянного тока независимого возбуждения путем переключения сопротивлений в якоре практически не применяется. Поэтому энергетические соотношения для этого способа пуска не рассматриваются.

Торможение двигателя постоянного тока независимого возбуждения можно выполнить изменением напряжения на якоре или перевести двигатель в режим динамического торможения.

При изменении напряжения на якоре можно получить любой закон движения, например, оптимальный по быстродействию или оптимальный по затратам энергии. В первом случае момент двигателя в режиме торможения устанавливается равным М_ДОП и поддерживается на заданном уровне во время торможения.

Затраты энергии без учета потерь вычисляются по выражению (4.1), в режиме торможения возможны случаи когда затраты получаются со знаком « – », то есть энергия возвращается в сеть. Потери энергии вычисляются при оптимальном по быстродействию законе движения по формуле (4.3), а при оптимальном по минимуму затрат по формуле (4.4).

Динамическое торможение не позволяет получить постоянство момента при торможении и при  = 0 М = 0, в настоящее время для двигателей постоянного тока независимого возбуждения применяется крайне редко.

4.2.ПУСК И ТОРМОЖЕНИЕ ДВИГАТЕЛЕЙ ПОСЛЕДОВАТЕЛЬНОГО ВОЗБУЖДЕНИЯ.

Аналогично двигателю независимого возбуждения пуск двигателя последовательного возбуждения можно выполнить путем изменения напряжения на двигателе или путем переключения сопротивления в цепи якоря.

Можно, устанавливая определенный закон изменения напряжения на двигателе, получить заданный закон движения до установившегося значения скорости. Поэтому формулы для расчета затрат и потерь энергии для двигателя независимого возбуждения можно применять для расчета режима пуска двигателя последовательного возбуждения, при этом сопротивление обмотки возбуждения входит в общее сопротивление якорной цепи.

Второй способ пуска – путем ввода добавочных сопротивлений в цепь ротора. Как известно, при включении добавочного сопротивления в цепь якоря механическая характеристика двигателя независимого возбуждения с увеличением сопротивления перемещается к оси М(I). На рис. 4.2. кривая 3 – естественная механическая характеристика. Кривые 1 и 2 соответствуют включению в цепь якоря добавочного сопротивления, причем R_ДОБ2 для кривой меньше R_ДОБ1.

Заданы значения токов переключения I₁ и I₂ причем I₁ > I_CT и I₂< I_ДОП. Пуск выполнятся следующим образом: подается напряжение на двигатель, у которого в цепь якоря включено сопротивление R_ДОБ1. Так как М > М_С то двигатель начинает разгоняться по кривой 1 пока ток не упадет до значения I₁, сопротивление в цепи якоря изменяетсядозначенияR_ДОБ2идальшеразгонпроисходитпо кривой 2. При уменьшении тока до значения I₁ шунтируется добавочное сопротивление в цепи якоря и далее разгон выполняется по естественной характеристике.

Для определения пусковых сопротивлений воспользуемся соотношением, полученным в разделе 3.4.

(4.5)

где R – суммарное сопротивление в цепи двигателя.

Обозначим R₁ сопротивление цепи якоря на первой пусковой характеристике Очевидно, что , а

(4.6)

где Ф₁ – поток, соответствующий току I₁

.

Величина КФ₁ может быть найдена по данным естественной характеристики

(4.7)

аналогично

.

Но для пусковой характеристики 2, когда сопротивление цепи двигателя равноR₂

(4.8)

Следовательно, из равенства (4.6) и (4.8) можно получить

(4.9)

Обозначив отношение , можно записать соотношение

(4.10)

Таким образом, можно сформулировать следующий порядок расчета сопротивлений в цепи двигателя последовательного возбуждения для осуществления пуска двигателя.

1. Выбираем токи переключения сопротивлений, I₂ < I_ДОП, I₁ > I_Е. Очевидно, чем больше разность I₂ – I₁, тем больше ступеней, но плавней пуск.

2. По универсальной естественной характеристике определяем значение скорости _е1 и _е2, соответствующие токам двигателя I₁ и I₂

1. Вычисляется величина

.

2. Вычисляется сопротивление цепи двигателя на 1 пусковой характеристикеR₁ = U/I₂.

3. Вычисляется сопротивление на последующей пусковой характеристике по значению сопротивления на предыдущей

4. Расчет ведут пока величина R_i+1 > R_Д, когда R_i+1 < R_Д расчет прекращают и количество ступеней пуска равно i.

Время пуска двигателя постоянного тока последовательного возбуждения при переключении сопротивлений определяется путем суммирования времени пуска на каждой ступени. Аналитически приближенно время пуска на i-той ступени определяется путем аппроксимации характеристики М = f() на этой ступени гиперболой при изменении скорости от _i до _i+1. Величины _i – скорость при включении i-того сопротивления пуска, _i+1 – скорость при переключении на следующую ступень определяются из выражения (4.5).

(4.11)

Моменты двигателя, соответствующие токам I₁ и I₂ определяются из выражений

(4.12)

Коэффициенты гиперболы К_i и ₁, проходящей через точки _i+1, _i, М1, М₂ на i-той ступени пуска находят из условий

(4.12)

Откуда

(4.14)

Тогда время пуска на i-той ступени определяется согласно выводам раздела 2

(4.15)

Торможение двигателя постоянного тока осуществляется включением добавочного сопротивления в цепь якоря и шунтированием якоря добавочным сопротивлением.

Расчет времени торможения и потерь выполняется аналогично расчету пуска двигателя последовательного возбуждения.

Если М_С = const, то

(4.16)

Время пуска

где n – число пусковых ступеней, включая разгон по естественной характеристике.

Переменные потери энергии при пуске на каждой пусковой ступени равны

(4.17)

Для вычисления зависимости I_i() на ступени пуска аппроксимируется гиперболой

(4.18)

Коэффициенты f_i и f_i можно вычислить так как мы знаем ток на границах ступени пуска, тогда на каждой ступени

(4.19)

Откуда, обозначив , получим

(4.20)

Так как

(4.21)

4.3. ПУСК И ТОРМОЖЕНИЕ ЭЛЕКТРОПРИВОДА НА БАЗЕ АСИНХРОННОГО ДВИГАТЕЛЯ.

4.3.1. Прямой пуск асинхронного короткозамкнутого двигателя – наиболее часто встречающийся в настоящее время способ пуска асинхронного двигателя с короткозамкнутым ротором. Если механическая характеристика двигателя задана формулой Клоса (см. раздел 3), то при известной зависимости момента сопротивления от скорости время пуска наиболее точно определяется путем интегрирования

(4.16)

гдеJ – суммарный момент инерции механической части электропровода;

М() – зависимость момента двигателя от скорости;

М_С() – зависимость момента сопротивления от скорости.

Учитывая, что  = ₁(1 – s) и

,

получаем

(4.17)

где ₁ – скорость изменения поля статора;

М_МАХ – максимальный момент асинхронного двигателя;

s_КР – критическое скольжение;

s_УСТ – установившееся значение скольжения;

(s) – момент сопротивления в функции скольжения в относительных единицах.

Так как теоретическое время достижения установившегося режима равно , то вводят коэффициент К = 1,02 … 1,05, то есть К определяет значение скольжения при котором процесс пуска можно считать законченным.

Переменные потери мощности во время пуска для асинхронного двигателя

(4.18)

или с учетом зависимости момента двигателя от скольжения

(4.19)

Так как потери энергии от переменных потерь мощности за время пуска

,

то, учитывая, что 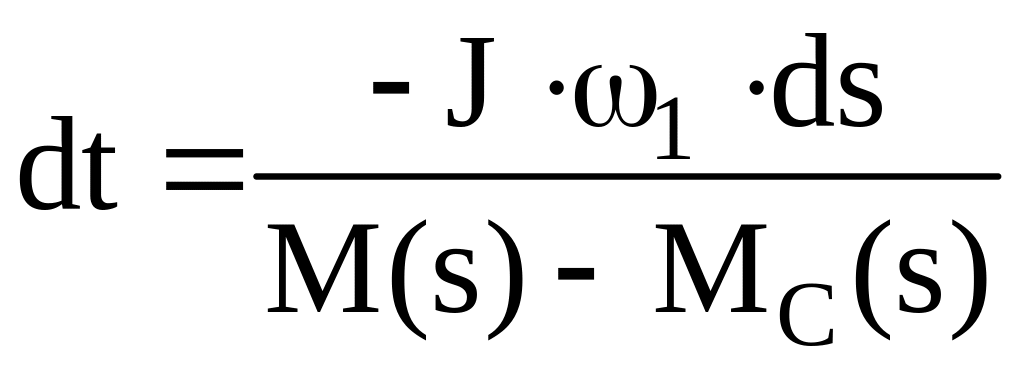, получаем

(4.20)

где J – суммарный момент инерции;

s_УСТ – установившееся значение скольжения.

Если зависимость М(s) задана приближенной формулой Клоса, то коэффициент s_КР определяется из условия, что М(s) проходит через точку М = М_ПУСК и s = 1.

Вычисление интегралов (4.17) и (4.20) производят приближенно графоаналитическим методом либо используя математические программы персонального компьютера. Например, ниже для вычисления этих интегралов используется программа MathCad.

Если момент сопротивления не зависит от скорости, то для приближенного определения времени пуска и потерь энергии можно использовать приведенные ниже графики рис. 4.3 и рис. 4.4.

Решение задачи в этом случае выполняется следующим образом:

1. Определяется критическое скольжение двигателя – s_КР.

2. Определяется отношение максимального момента к моменту сопротивления

.

3. Для получения значений _П и s_КР по графикам на рис. 4.3 определяется величина .

4. Определяется механическая постоянная привода

,

где J – суммарный момент инерции механической части привода; ₁ угловая скорость изменения напряжения статора.

5. Время пуск определяется по формуле

.

6. Для значения _П и s_КР по графикам на рис. 4.4 определяется величина .

7. Вычисляется кинетическая энергия

8. Переменные потери за время пуска

.

4.3.2 Торможение асинхронного двигателя противовключением.

Расчет времени торможения ведется по выражению (4.17). Пределы интегрирования равны

(4.21)

где s_УСТ – установившееся значение скольжения двигательного режима.

Момент сопротивления в этом случае изменяет знак.

Аналогично определяются переменные потери энергии, используются выражения (4.20) с пределами интегрирования (4.21). Учитывается также то, что момент сопротивления при торможении изменяет знак.

Если момент сопротивления не зависит от скорости и в режиме торможения он положителен, то для приближенного определения времени пуска и потерь энергии можно использовать графики, приведенные на рис. 4.5 и 4.6. Расчет ведется аналогично предыдущему случаю.

4.3.3. Пуск и торможение АД с фазным ротором путем переключения сопротивлений ротора.

При увеличении сопротивления ротора механическая характеристика асинхронного двигателя поворачивается по часовой стрелке вокруг точки М = 0, s = 0. Величина критического скольжения при этом равна (см. главу 3)

(4.22)

Таким образом, при различных сопротивлениях в цепи ротора получаем семейство механических характеристик рис. 4.7. Задаваясь значениями моментов переключения М₁ и М₂ можно осуществить запуск АД. Сначала включается сопротивление R_ДОБ и двигатель разгоняется до скорости ₁ (скольжение s₁), затем включается в ротор сопротивление R_4ДОБ и рабочая точка перемещается по механической характеристике 4 до достижения скоростью величины ₂ (скольжение s₂) и т.д. до выключения всех добавочных сопротивлений. В конце пуска рабочая точка перемещается по естественной характеристике до достижения устойчивого режима.

Предполагая, что в рабочей области механическая характеристика двигателя линейная, можно записать, что конечное значение скорости на i-том участке разгона

где ₀ – скорость поля статора или скорость АД при идеальном холостом ходе.

Откуда число ступеней пуска приближенно может быть определено

(4.23)

если задано число ступеней, то отношение моментов переключения

(4.24)

При определении числа ступеней по (4.23) n округляется до ближайшего большего значения, а величина М₁ должна быть больше М_С. Чем больше число ступеней тем меньше скачки момента и тем плавней осуществляется разгон механизма.

Приближенно расчеты величин добавочных сопротивлений выполняют, используя приближенную формулу Клоса (считая величину ).

В этом случае уравнение i-той пусковой характеристики, проходящей через точку s_i и M₂, определяется как

;(4.25)

s_e

где s_Ki – скольжение на i-той пусковой характеристике;

s_i – скольжение при М = М₂.

Значение скольжения s_i+1 при М = М₁, тогда определится из выражения

(4.26)

При постоянстве момента, исходя из упрощенной формулы Клоса для любой пусковой характеристики и естественной характеристики, можно записать равенство

где s_Ke – критическое скольжение на естественной характеристике;

s_e – скольжение соответствующее заданному моменту на естественной характеристике;

s_u – то же, но на пусковой характеристике.

Очевидно, что равенство будет выполняться только тогда, когда

,

или

(4.27)

Расчет величины роторного сопротивления ведут в следующей последовательности:

1. Задаются значениями моментов переключения М₁ и М₂. Например, выбирается М₁ = 1,1М_МАХ, М₂ = 0,9 М_МАХ. Если задано время пуска, то М₁ М₂ уточняют в дальнейшем из условия, что время пуска равно заданному значению.

2. Определяют скольжение s_e, как величину установившегося значения при R_2ДОБ = 0 и М = М₁

гдеs_Ke – критическое скольжение на естественной характеристике;

₁ – отношение М_МАХ / М₁.

Величина s_Ke может быть определена по формуле

;

где – отношение максимального момента к номинальному;

s_HOM – номинальное скольжение двигателя;

3. Определяют коэффициент а.

;

где ₂ – отношение М_МАХ / М₂.

4. Определяют коэффициент b.

;

где ₁ – отношение М₁ / М_МАХ .

5. Определяют критическое скольжение на первой реостатной характеристике

s_K1 = as, так как s₁ = 1то s_K1 = a.

6. Определяем скольжение s_P1 при котором происходит переключение на вторую пусковую характеристику

.

7. Аналогично выполняют расчет для второй и последующих пусковых характеристик

…

…

Вычисления ведут до тех пор пока s_Pi+1  s_Ke.

8. Величины сопротивления ротора в сумме с добавочным

а) номинальное активное сопротивление ротора

б) сопротивление цепи ротора на i-той пусковой характеристике

.

Потери мощности при управлении путем ввода сопротивления в цепь ротора складываются из переменных потерь, включающих потери в меди статора, ротора и во внешних резисторах роторной цепи, и постоянных, не зависящих от нагрузки.

К последним относятся потери в стали статора и ротора, а также механические и добавочные, обусловленные полями рассеяния .и высшими гармониками МДС статора и ротора. Потери в стали статора в данном случае остаются постоянными независимо от скольжения, так как напряжение, подводимое к статору, не изменяется.

Механические потери приблизительно пропорциональны угловой скорости, с увеличением скольжении уменьшается, при этом потери в стали ротора возрастают вследствие увеличения частоты тока ротора, поэтому можно приближенно считать, что сумма постоянных потерь останется неизменной независимо от нагрузки и скорости привода.

Сумма же переменных потерь мощности может быть найдена по формуле

(4.28)

из (4.27) получаем

(4.29)

Тогда с учетом (4.29)

(4.30)

Таким образом, при неизменном моменте нагрузки и реостатном управлении потери мощности в роторной цепи изменяются пропорционально скольжению, а потери в статоре не зависят от скольжения и остаются неизменными при данном моменте нагрузки.

Напомним, что основная мощность теряется в регулировочном резисторе. Если, например, скорость двигателя снижена вдвое по сравнению с номинальной, то примерно половина всей потребляемой из сети мощности теряется в регулировочных резисторах.

Иначе оцениваются потери мощности в меди статора и ротора при вентиляторной нагрузке. Для упрощения будем считать, что вентиляторная характеристика выражается квадратичной зависимостью момента нагрузки от угловой скорости, а момент холостого хода вентилятора не учитывается. Тогда

Кроме того,

(4.32)

Подставляя эти значения в (4.30), получаем

(4.33)

Первый член (4.33) определяет потери мощности в роторной цепи от скольжения

(4.34)

где Р_НОМ – номинальная мощность двигателя.

Из (4.33) следует, что при s = 0 и s = 1 потери мощности в роторной цепи Р₂ = 0.

Анализ (4.51) показывает, что максимум потерь мощности в роторной цепи при вентиляторной нагрузке имеет место при и составляет

(4.45)

Например, при s = 0,02P_2MAX = 0,16P_HOM. Потери мощности в меди статора при вентиляторной нагрузке (без учета потерь от тока холостого хода) равны:

(4.36)

или

.

Из (4.36) следует, что при s, изменяющемся от 0 до s_НОМ, Р₁ изменяется от 0 до .

На рис. 4.8. приведены кривые относительных потерь мощности и при реостатном регулировании и вентиляторной нагрузке. Суммарные потери мощности при регулировании угловой скорости равны:

(4.37)

где Р_пост – постоянные потери.

Обычно привод работает на различных регулировочных характеристиках неодинаковое время. В этом случае потери энергии за регулировочный цикл следует определять с учетом продолжительности работы на каждой характеристике, поэтому

(4.38)

где Р₁, Р₂ …Р_n, t₁, t₂ …t_n – соответственно суммарные потери мощности и продолжительность работы привода на первой, второй……n-й регулировочных характеристиках.

Зная полезную мощность, развиваемую приводом на каждой регулировочной характеристике, можно найти к.п.д. привода за цикл пуска

(4.39)

Следует отметить, что энергетические показатели регулируемого электропривода за цикл зависят от режима работы. При продолжительном режиме они существенно ниже, чем при повторно-кратковременном. В обоих случаях они тем выше, чем меньше диапазон регулирования и чем большую часть времени привод работает на повышенных скоростях.

Недостатками реостатного регулирования скорости являются: 1) необходимость дискретного изменения сопротивления в роторной цепи с помощью силовых аппаратов, управляемых дистанционно или вручную, что дает ступенчатое регулирование скорости и исключает возможность использования замкнутых систем автоматического управления; 2) невысокое быстродействие; 3) большие потери энергии.

Реостатное регулирование благодаря своей простоте находит практическое применение, например, в приводе подъемно-транспортных устройств, вентиляторов и насосов малой и средней мощности (до 100 кВт).