Формула Бернулли.

Если производится п независимых испытаний, в каждом из которых вероятность появления события А равна р, а вероятность его не появления равна q = 1- р, то вероятность того, что событие А произойдет т раз определяется формулой Бернулли

, т=0, 1, 2,…,n.

Если в серии из п независимых опытов, в каждом из которых может произойти одно и только одно из k событий А₁, А₂, … ,А_k с соответ­ствующими вероятностями p₁, p₂, ..., p_k , то вероятность того, что в этих опытах событие А₁ появится m₁ раз, событие А₂— m₂ раз, ..., событие А_k — m_k раз, равна

,

где m₁+m₂+...+m_k = n. Полученная формула называются полиноми­альным распределением.

- 11 -

Пример 1.31. Производится три независимых выстрела по цели. Веро­ятности попадания при разных выстрелах одинаковы и равны р=0,9. Какова вероятность: а) промаха; б) одного попадания; в) двух попаданий; г) трех попаданий?

Решение. В данном случае n=3; р=0,9; q=0,1. Пользуясь формулой Бернулли, находим:

а) Р₃(0) = • 0,9⁰ • 0,1³ = 0,001 — вероятность трех промахов;

б) Р₃(1) = • 0,9¹ • 0,1² = 3 • 0,9 • 0,01 = 0.027 — вероятность одного попадания;

в) Р₃(2) = • 0,9² • 0,1¹ = 3 • 0,81 • 0,1 = 0,243 – вероятность двух попаданий;

г) Р₃(3) = • 0,9³ • 0,1⁰ = 0,9³ = 0,729 — вероятность трех попаданий.

Э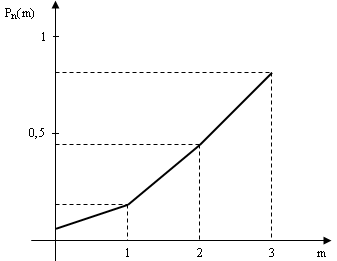 ти результаты можно изобразить графически, отложив на оси Ох - значения m, на оси Оy — значения Р_n(m) (рис. 14).

Ломаная, соединяющая точки (0; 0,001), (1; 0,027), (2; 0,243), (3; 0,729), называется многоугольником распределения вероятностей.

Пример 2. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три из шести? Ничьи во внимание не принимаются.

Решение. Играют равносильные шахматисты, поэтому вероятность выигрыша ; следовательно, вероятность проигрыша . Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли. Найдем вероятность того, что две партии из четырех будут выиграны: .

Найдем вероятность того, что три партии из шести будут выиграны: .

Следует, что Р₄ (2) > Р₆(3), т. е. 2 из 4.

-12 -

Задачи для самостоятельного решения.

1. Монету подбрасывают 10 раз. Какова вероятность того, что герб выпадет (появится): а) 4 раза; б) ни разу, в) хотя бы один раз?

2. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз; б) не менее двух раз?

3. В семье трое детей. Какова вероятность того, что: а) все они маль­чики; б) один мальчик и две девочки? Считать вероятность рожде­ния мальчика 0,51. а девочки — 0,49.

4. В семье пять детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков; в) более двух мальчиков; г) не менее двух и не более трех мальчиков? Вероятность рождения мальчика принять равной 0,51.

5. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырех; б) выиграть не менее двух партий из четырех или не менее трех партий их пяти? Ничьи во внимание не принимаются.

6. Отрезок АВ разделен точкой С в отношении 2:1. На этот отрезок наудачу брошены четыре точки. Найти вероятность того, что две из них окажутся левее точки С и две – правее?

7. На отрезок АВ длины a наудачу брошено пять точек. Найти вероятность того, что две точки будут находится от точки А на расстоянии, меньшем х, а три – на расстоянии, большем х?

8. а) Найти вероятность того, что событие А появится не менее трех раз в четырех независимых испытаниях, если вероятность появления события А в одном испытании равна 0,4?

б) событие В появится в случае, если событие А наступит не менее четырех раз. Найти вероятность наступления события В, если будет произведено пять независимых испытаний, в каждом из которых вероятность появления события А равна 0,8?

9. В каждой урне (их 2) лежит по 10 шаров. Наудачу выбирается урна и извлекается один шар без возвращения в урну. При очередном выборе одна урна оказалась пустой. Найти вероятность того, что во второй урне осталось 6 шаров?

10. Устройство состоит из трех независимо работающих основных элементов. Устройство отказывает, если откажет хотя бы один элемент. Вероятность отказа каждого элемента за время t равна 0,1. Найти вероятность безотказной работы устройства за время t, если работают только основные элементы?

- 13 -