Теорема сложения и умножения вероятностей.

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий: P(А + В) = Р(А) + Р(В), АВ = .

Теорема сложения вероятностей совместных событий. Вероятность суммы двух совместных событий равна сумме их вероятностей без вероятности их произведения: Р(А + В) = Р(А) + Р(В)-Р(АВ).

Теорема умножения вероятностей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло: Р(АВ) = Р(А)Р(ВА)=Р(В)-Р(АВ).

Для независимых событий правило умножения вероятностей принимает вид: Р(АВ) = Р(А)Р(В)

т. е. вероятность произведения двух независимых событий равна про­изведению вероятностей этих событий.

Условной вероятностью события В при условии, что произошло событие А, называется отношение вероятности произведения этих со­бытий к вероятности события А, причем Р(А)≠0, обозначается сим­волом Р(В|А). Таким образом, по определению P(A)≠0.

Пример 1. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем пять из них в переплете. Библиотекарь берет наудачу три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете (событие А)?

Решение. Решим задачу двумя способами.

Первый способ. Требование – хотя бы один из трех взятых учебников в переплете – будет осуществлено, если произойдет любое из следующих трех несовместных событий: B – один учебник в переплете, C - два учебника в переплете, D - три учебника в переплете. Интересующее нас событие А можно представить в виде суммы событий: А = В+С+D. По теореме сложения получаем, P(A)=P(B)+P(C)+P(D) (*). Найдем вероятности событий B, C, D:

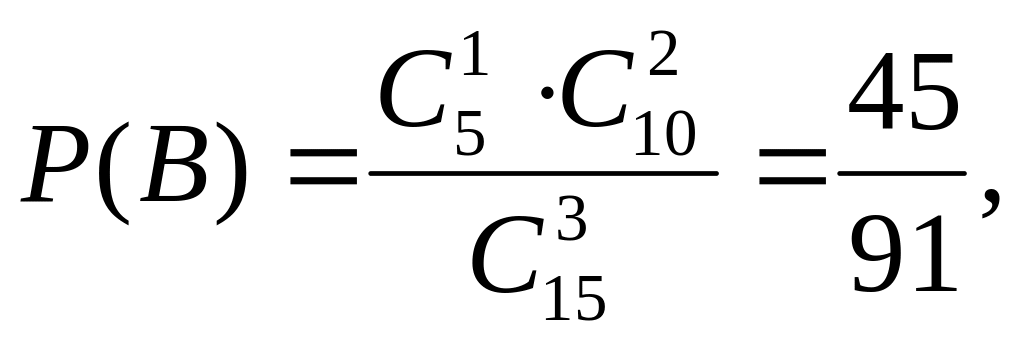
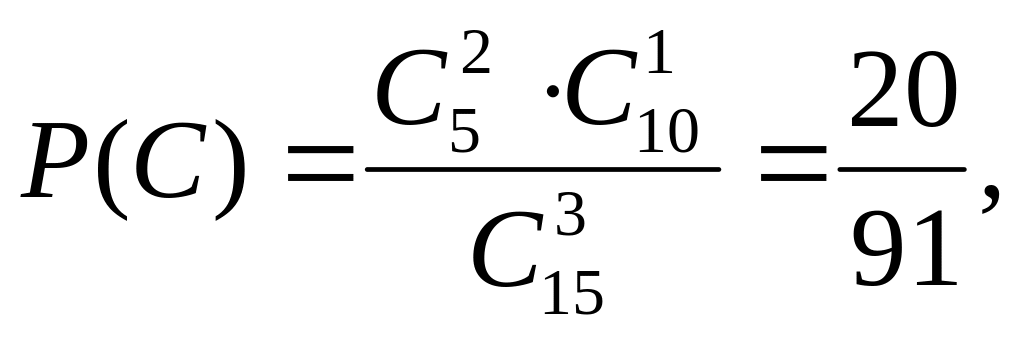
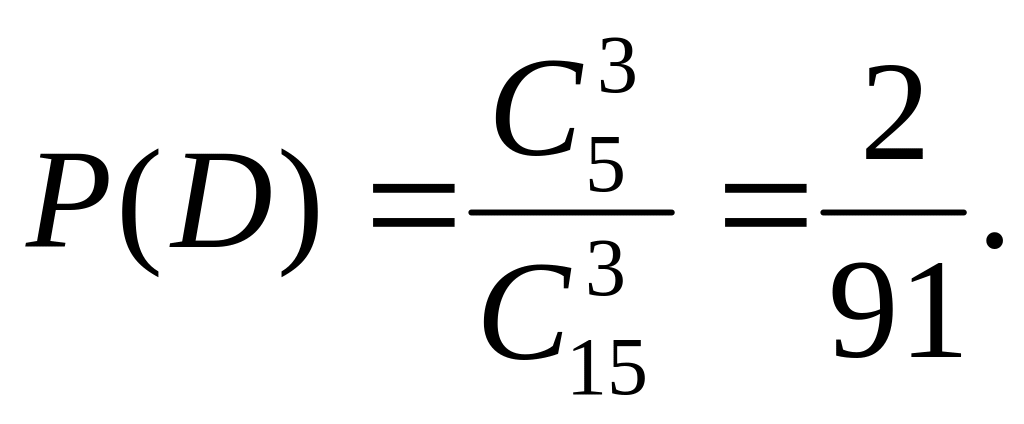
- 3-

Подставим эти вероятности в равенство (*) и окончательно получим

Второй способ. События А (хотя бы один из взятых трех учебников имеет переплет) и Ā (ни один из взятых учебников не имеет переплета) – противоположные, поэтому P(A) + P(Ā)=1 (сумма вероятностей двух противоположных событий равна единице). Отсюда P(A) =1 - P(Ā). Вероятность появления события Ā, 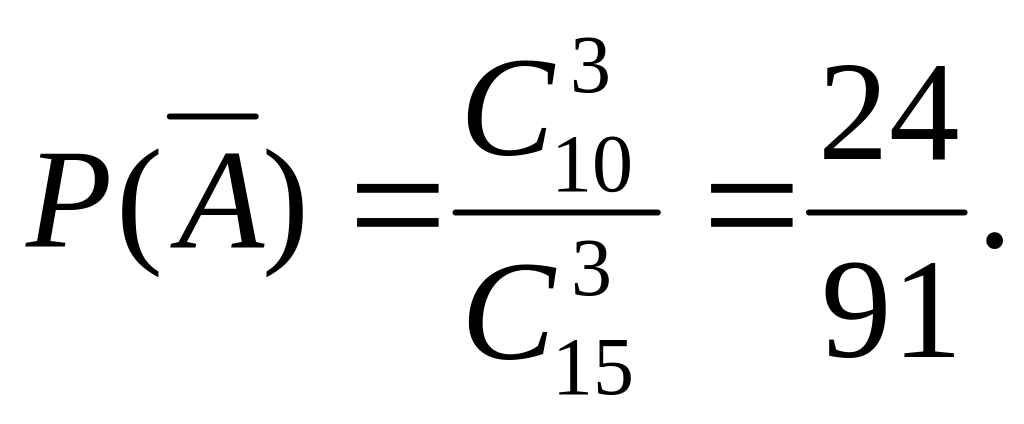Искомая вероятность

Пример 2. Бросаются две игральные кости. Какова вероятность появления хотя бы одной шестерки?

Решение. Введем события: А - появление шестерки на первой кости, В - на второй кости. Тогда А + В - появление хотя бы одной шестерки при бросании костей. События A и В совместные. По формуле сложения вероятностей совместных событий, находим . (Решим задачу иначе: найдем вероятность появления хотя бы одной шестерки, используя нахождение вероятности противоположного события - в результате бросания ни одной шестерки не выпало, . Следовательно, .)

Пример 3. В коробке находится 4 белых, 3 синих и 2 черных шара. Наудачу последовательно вынимают 3 шара. Какова вероятность того, что 1-й шар будет белым, 2-й — синим, 3-й — черным?

Решение. Введем следующие события: A₁ — первым вытащили белый шар, А₂ — вторым — синий, А₃ — третьим — черный. Тогда интересую­щее нас событие А представится в виде А= A₁ А₂  А₃. По прави­лу умножения вероятностей Р(А)=Р(А₁)Р(А₂А₁) Р(А₃А₁ А₂). Но ; , так как шаров осталось 8, а число благоприятных случаев для события А₂ равно 3; Р(А₃А₁ • А₂) = , так как уже два шара (белый и синий) вытащены. Следовательно, .

- 4-

Пример 4. Производится выбор (наудачу) флага из четырех, имеющихся в наличии: красного, голубого, белого и трехцветного (красно-бело-голубого). Исследовать на независимость события: К- выбранный флаг имеет красный цвет, Г- имеет голубой цвет; Б -имеет белый цвет.

Решение. Возможных исходов выбора 4: событию К благоприятствуют 2 исхода (красный цвет имеется у двух флагов). Поэтому . Аналогично находим, что . Событию КГ- выбран флаг, имеющий 2 цвета (красный и голубой), — благоприятствует один исход. Поэтому, . И так как , то события К и Г независимы. Аналогично убеждаемся в независимости: событий К и Б, Б и Г. Стало быть, события К, Б, Г попарно независимы. А так как , то события К, Г и Б не являются независимыми в совокупности.

Пример 5. В урне 2 белых и 7 черных шаров. Из нее последовательно вынимают два шара. Какова вероятность того, что 2-й шар окажется белым при условии, что 1-й шар был черным?

Решение. Решим задачу двумя способами.

1. Пусть А — 1-й шар черный, В — 2-й шар белый. Так как событие А произошло, то в урне осталось 8 шаров, из которых 2 белых. Поэтому .

2. Найдем Р(ВА) по формуле условной вероятности. Очевидно, что . Находим Р(АВ): n = 98 = 72 -— общее число исходов (появление двух шаров). Событию АВ благоприятствуют исходов. Поэтому . Следовательно, .