Набор тестов
Тест 1. Проверка подпрограммы-процедуры нахождения численного значения интеграла.
Пусть входные данные имеют следующие значения: нижний предел интегрирования C=0.81; верхний предел интегрирования D=0.62.
Результаты контрольного просчёта: численное значение интеграла B=-1.349.
Тест 2. Проверка ветви, вычисляющей значении функции.
Пусть входные данные имеют следующие значения: параметр функции A=5; аргумент X=4.
Результаты контрольного просчёта: численное значение интеграла B=-1.349; значение функции Y=-3.56.
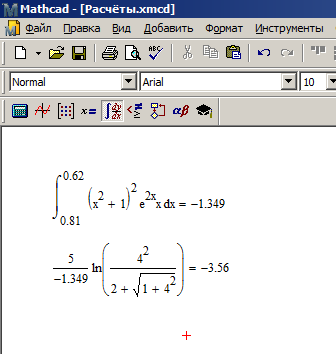
Текст программы на языке программирования Pascal и результаты её выполнения
program TabRgr;
{Студент: Маренков Е.В., группа: 4О-110Б, дата: 08.12.12}
{Программа табулирования функции Y=f(A,B,X), где аргумент X принимает M значений, параметр A изменяется от начального An с шагом Da, N количество раз, а параметр B равен численному значению определённого интеграла функции (x*x+1)*(x*x+1)*(exp(2*x))*x с верхней границей интегрирования, равной 0.62, и нижней 0.81, при заданной погрешности Eps}
const Nmax=20;
type Tmy=array [1..Nmax,1..Nmax] of real;
Tmx=array [1..Nmax] of real;
Ter=array [1..Nmax,1..Nmax] of integer;
var ma,mx:Tmx;
my:Tmy;
er:Ter;
an,da,b2,b1,eps,c,d:real;
n,m,km,ki1,ki2,err1,err2:integer;
{Процедура ввода массива X}
procedure VvodX(m:integer; var mx:Tmx);
var
i:integer;
begin
writeln('Введите массив значений x');
for i:=1 to m do
readln (mx[i]);
end;
{Процедура вычисления массива ma}
procedure DataIn(an,da:real; n:integer; var ma:Tmx);
var
a:real;
i:integer;
begin
a:=an;
for i:=1 to n do
begin
ma[i]:=a;
a:=a+da;
end;
end;
{Функция вычисления интегральной функции}
function F(x:real):real;
begin
F:=(x*x+1)*(x*x+1)*(exp(2*x))*x;
end;
{Интеграл методом трапеций}
procedure IntegralTrap(c,d,eps:real; km:integer; var err,ki:integer; var Int1:real);
var
Int,x,y1,yn,Del,H :real;
i,j,k:integer;
begin
err:=1;
Int1:=0;
y1:=F(c);
yn:=F(d);
k:=2;
for j:=1 to km do
begin
Int:=0;
H:=(d-c)/k;
x:=c+H;
i:=1;
repeat
Int:=Int+F(x);
Inc(i);
x:=x+H;
until i>=k;
Int:=H*(y1/2+yn/2+Int);
Del:=abs(Int-Int1);
Int1:=Int;
k:=k*2;
if del<eps then
begin
err:=0;
ki:=j;
j:=km;
end;
end;
end;
{Интеграл методом Симпсона}
procedure IntegralSim(c,d,eps:real; km:integer; var err,ki:integer; var int:real);
var
k,int1,y1,yn,s4,s2,h,del,x:real;
i,j:integer;
begin
int1:=0;
y1:=F(c);
yn:=F(d);
k:=2;
Err:=1;
for j:=1 to km do
begin
int:=0;
h:=(d-c)/k;
s4:=0;
s2:=0;
i:=1;
x:=c+h;
repeat
if odd(i) then s4:=s4+F(x) else s2:=s2+F(x);
int:=h*(y1+yn+4*s4+2*s2)/3;
inc(i);
x:=x+h;
until i>=k;
del:=abs(int1-int);
if del<eps then
begin
err:=0;
ki:=j;
j:=km;
end
else
begin
int1:=int;
k:=k*2;
end;
end;
end;
{Процедуры табулирования}
procedure Tab(b: real; var ma,mx:Tmx; var my:Tmy; var er:Ter);
var
i,j:integer;
begin
for i:=1 to n do
for j:=1 to m do
my[i,j]:=ma[i]/b*ln(mx[j]*mx[j]/(2+sqrt(1+mx[j]*mx[j])));
end;
{Процедура вывода даннных}
procedure ResOut(n,m:integer; ma,mx:Tmx; my:Tmy; er:Ter);
var
i,j:integer;
begin
for i:=1 to n do begin
writeln();
write('a=',ma[i]:2:4);
writeln();
for j:=1 to m do
if er[i,j]=1 then writeln(' x=',mx[j]:2:2, ' ошибка в данных') else
writeln(' x=',mx[j]:2:2,' y=',my[i,j]:2:4);
end;
readln;
end;
{Начало главной программы}
begin
writeln('Введите кол-во значений x');
readln(m);
VvodX(m,mx);
writeln('Введите значения an,da,n');
readln(an,da,n);
writeln ('Введите значения нижнего предела интегрирования C, верхнего предела интегрирования D');
readln(c,d);
writeln ('Введите значения погрешности Eps, предельного числа повторения циклов Km');
readln(eps,km);
DataIn(an,da,n,ma);
IntegralSim(c,d,eps,km,err1,ki1,b1);
IntegralTrap(c,d,eps,km,err2,ki2,b2);
If err1=0 then
begin
writeln ('Численное значение определенного интеграла методом Симпсона B=',b1:5:7,', количество итераций (KI) = ',ki1);
writeln ('Численное значение определенного интеграла методом трапеций B=',b2:5:7,', количество итераций (KI) = ',ki2);
Tab(b1,ma,mx,my,er);
ResOut(n,m,ma,mx,my,er);
end
else
writeln ('Численное значение интеграла не найдено за Km=',Km);
end.
end.
Выводы
Анализ результатов выполнения программы показывает, что полученные значения функции совпадают с результатами, полученными для контрольный тестовых примеров с помощью калькулятора, что подтверждает работоспособность программы. Следовательно, программа правильно вычисляет заданную функцию по всем ветвям алгоритма и может быть использована для других значений аргументов и параметров функции.