Московский авиационный институт

(государственный технический университет)

Факультет радиоэлектроники

Кафедра 403

Разработка алгоритмов и программ решения алгебраических задач численными методами

Расчетно-графическая работа по дисциплине «Информатика»

Вариант №11

Выполнил:

Студент группы 4О-110Б

Маренков Е.

Принял:

преподаватель кафедры 403

Кошелькова Л.В.

Москва

2012 г.

Содержание

Задание	2
Анализ задания	2
Теоретические сведения	3
Схемы алгоритмов	4
Набор тестов	13
Текст программы на языке программирования Pascal и результаты её выполнения	14
Выводы	18
Список использованной литературы	19

1. Задание

Разработать схему алгоритма, составить Pascal-программу вычисления таблицы значений функции при заданных изменениях значений аргумента X и параметра A. Параметр B принимает значение, численно равное интегралу .

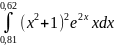2. Анализ задания

Входные данные:

1. M – количество значений аргумента X, тип – целый;

2. Mx – массив значений аргумента X, тип - вещественный;

3. An – начальное значение параметра А, тип – вещественный;

4. Da – шаг изменения значений параметра A, тип – вещественный;

5. N – количество значений параметра A, тип – целый;

6. C – нижняя граница интегрирования, тип – вещественный;

7. D – верхняя граница интегрирования, тип – вещественный;

8. Eps – погрешность вычисления интеграла, тип – вещественный;

9. Km – предельное число повторений цикла, тип – целый.

Выходные данные:

1. Ma – массив значений параметра A, тип – вещественный;

2. My – двумерный массив значений функции Y, тип – вещественный;

3. Er – двумерный массив признака ошибки, тип – целый;

4. Err – признак ошибки при вычислении интеграла, тип – целый;

5. B – численное значение интеграла, тип – вещественный.

В алгоритме выполняются следующие функции:

• Ввод исходных данных;

• Вычисление таблицы значений функции;

• Вычисление значения определенного интеграла;

• Вычисление значения параметров функции;

• Проверка значения аргумента и формирование признака ошибки, если он имеет неположительное значение;

• Вывод результатов вычислений.

3. Теоретические сведения

Определённый интеграл – аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая - область во множестве задания этой функции (функционала).

Нахождение значения интеграла:

1. Нахождение первообразной функции;

2. Нахождения значений первообразной от нижней и верхней границы интегрирования;

3. Вычитание значения первообразной от нижней границы интегрирования из значения первообразной от верхней границы.

Используя три точки отрезка интегрирования, можно заменить подынтегральную функцию параболой. В качестве таких точек используют концы отрезка и его середину:

.

Если разбить интервал интегрирования на 2N равных частей, то имеем

где  .