Тема 7. Теория вероятностей. Основные законы распределения дискретных случайных величин. Интегральная теорема Лапласа
1. Случайная величина подчиняется нормальному закону с математическим ожиданием mx = 10 метров и со срединным отклонением Ех = 5 метров. Определить вероятность попадания случайной величины на участок (+13 метров, +21 метр).
+a: Р(+13 < X <+21) = 0,27393
-b: Р(+13 < X <+21) = 0,35543
-c: Р(+13 < X <+21) = 0,16574
2. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
1 |
3 |
р |
0,7 |
0,3 |
Тогда её функция распределения вероятностей имеет вид…
+a:
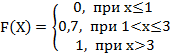
-b:
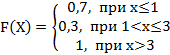
-c:
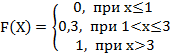
-d:
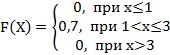
3. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
-3 |
3 |
р |
0,7 |
0,3 |
Тогда её функция распределения вероятностей имеет вид…
+a:
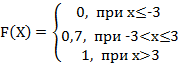
-b:
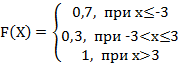
-c:
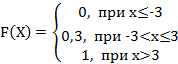
-d:
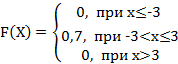
4. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
1 |
3 |
р |
0,2 |
0,8 |
Тогда её функция распределения вероятностей имеет вид…
+a:
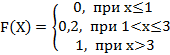
-b:
-c:
-d:
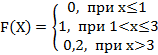
5. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
2 |
4 |
р |
0,8 |
0,2 |
Тогда её функция распределения вероятностей имеет вид…
+a:
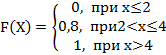
-b:
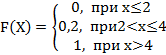
-c:
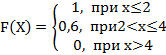
-d:
6. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
2 |
4 |
6 |
р |
0,1 |
0,2 |
0,7 |
Тогда её функция распределения вероятностей имеет вид…
-a: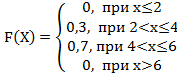
-b:
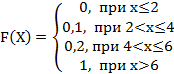
+c:
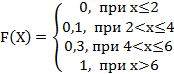
-d:
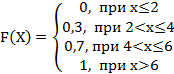
7. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
-1 |
3 |
7 |
р |
0,7 |
0,2 |
0,1 |
Тогда её функция распределения вероятностей имеет вид…
-a: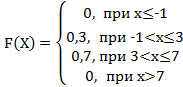
-b:
+c:
-d:
8. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
2 |
4 |
6 |
р |
0,3 |
0,3 |
0,4 |
Тогда её функция распределения вероятностей имеет вид…
-a:
-b:
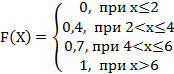
+c:
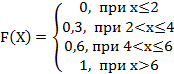
-d:
9. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
1 |
3 |
5 |
7 |
р |
0,4 |
0,3 |
0,2 |
0,1 |
Тогда её функция распределения вероятностей имеет вид…
+a: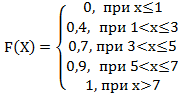
-b: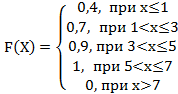
-c: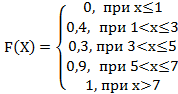
-d:
10. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
1 |
3 |
5 |
7 |
р |
0,6 |
0,2 |
0,1 |
0,1 |
Тогда её функция распределения вероятностей имеет вид…
+a: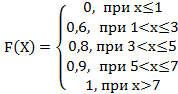
-b: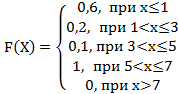
-c:
-d: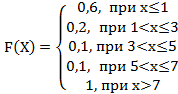
11. Дискретная случайная величина Х задана законом распределения вероятностей:
Х |
-2 |
2 |
6 |
10 |
р |
0,6 |
0,2 |
0,1 |
0,1 |
Тогда её функция распределения вероятностей имеет вид…
+a: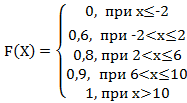
-b: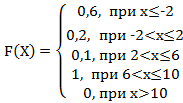
-c:
-d: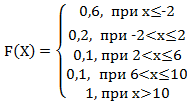
12. Для дискретной случайной величины Х:
Х |
2 |
3 |
4 |
5 |
р |
р1 |
р2 |
р3 |
р4 |
функция распределения вероятностей имеет вид…
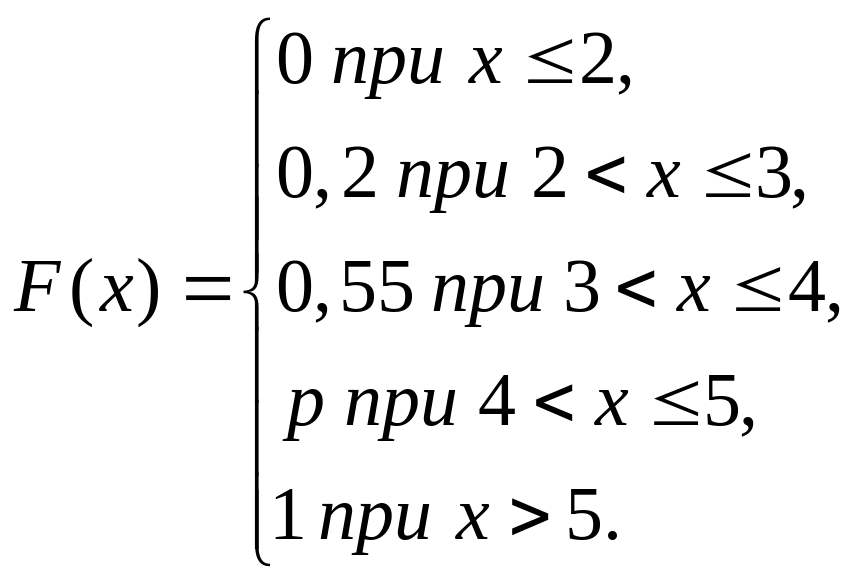
Тогда значение параметра р может быть равно...
-a: 0,25
-b: 1
+c: 0,655
-d: 0,45
Решение:
Следовательно р≥0,55 и р≤1. Этим
условиям удовлетворяет значение р=0,655.
13. Для дискретной случайной величины Х:
Х |
2 |
3 |
4 |
5 |
р |
р1 |
р2 |
р3 |
р4 |
функция распределения вероятностей имеет вид…
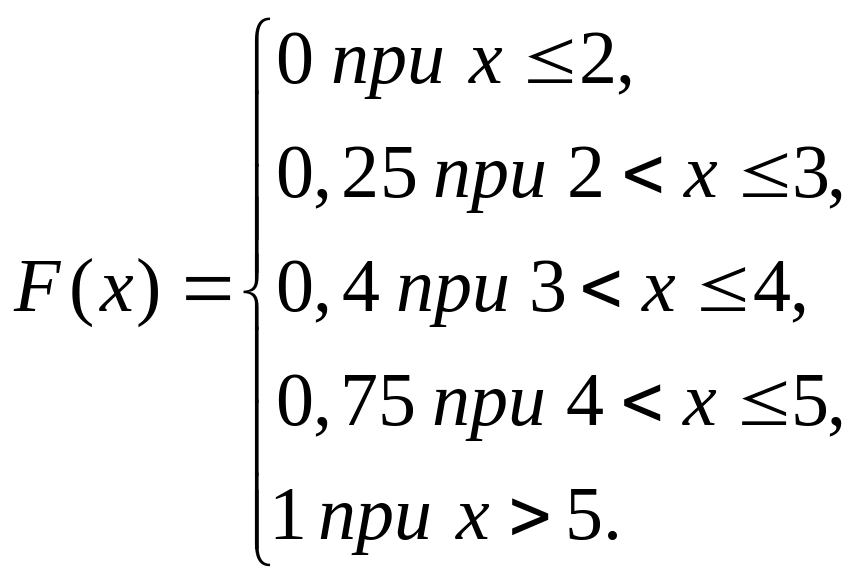
Тогда значения вероятностей р1, р2, р3 и р4 равны соответственно...
+a: 0,25; 0,15; 0,35; 0,25
-b: 0,25; 0,35; 0,15; 0,25
-c: 0,25; 0,25; 0,25; 0,25
-d: 0; 0,25; 0,4; 0,75
Решение: Следовательно р1=0,25; р3=0,75-0,4=0,35; и
р4=1-0,75=0,25.