Тема 14. Математическая статистика. Генеральная и выборочная совокупности

1. Статистическое распределение выборки имеет вид

Хi	-1	0	1	3
ni	4	6	3	7

Тогда относительная частота варианты x₂=0, равна…

-a: 6

+b: 0,3

-c: 0,35

-d: 0,5

2. Статистическое распределение выборки имеет вид

Хi	-2	1	3	4
ni	2	5	6	7

Тогда относительная частота варианты x₃=3, равна…

-a: 6

-b: 0,25

-c: 0,1

+d: 0,3

3. Статистическое распределение выборки имеет вид

Хi	-2	0	2	4
ni	4	6	1	9

Тогда относительная частота варианты x₂=0, равна…

-a: 0,5

+b: 0,3

-c: 0,55

-d: 6

4. Статистическое распределение выборки имеет вид

Хi	-4	-2	2	4
ni	7	3	6	4

Тогда относительная частота варианты x₃=2, равна…

+a: 0,3

-b: 0,4

-c: 6

-d: 0,1

5. По выборке объёма n=100 построена гистограмма частот: 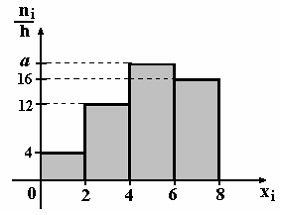Тогда значение а равно…

+a: a=18

-b: a=68

-c: a=21

-d: a=25

6. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,5576; 0,5547; 0,5307; 0,6429; 0,6005; 0,6054. Найти выборочную среднюю.

-a: 0,435

+b: 0,582

-c: 0,611

-d: 0,599

7. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,0276; 0,0651; 0,0233; 0,1598; 0,1826; -0,0245. Найти выборочную среднюю.

-a: 0,0435

-b: 0,0582

+c: 0,0631

-d: 0,0599

8. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,1609; 0,2638; -0,2454; 0,2765; 0,2427; 0,3286. Найти выборочную среднюю.

-a: 0,1435

-b: 0,1582

-c: 0,1611

+d: 0,1712

9. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,3789; -0,0648; -0,2961; -0,3738; -0,3763; -0,0614. Найти выборочную среднюю.

+a: -0,2586

-b: -0,2582

-c: -0,2611

-d: -0,2599

10. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,3819; 0,1483; 0,1934; 0,3645; 0,3836; 0,2264. Найти выборочную среднюю.

-a: 0,243

+b: 0,283

-c: 0,261

-d: 0,299

11. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,3588; 0,3695; 0,3373; 0,5235; 0,4872; 0,3703. Найти выборочную среднюю.

-a: 0,4043

-b: 0,4058

+c: 0,4078

-d: 0,4059

12. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,2091; -0,1739; -0,2105; -0,2196; -0,1584; -0,1515. Найти выборочную среднюю.

-a: -0,1435

-b: -0,1582

-c: -0,1611

+d: -0,1872

13. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,1044; -0,1092; -0,2121; -0,1707; -0,1664; -0,278. Найти выборочную среднюю.

+a: -0,1735

-b: -0,1582

-c: -0,1611

-d: -0,1599

14. Дана выборка из нормального распределения, дисперсия которого неизвестна:

1,0856; 0,7884; 0,9911; 0,82; 0,8975; 1,0073. Найти выборочную среднюю.

-a: 0,9243

+b: 0,9316

-c: 0,9261

-d: 0,9299

15. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,009; -0,1717; -0,1902; -0,3237; -0,1404; 0,044. Найти выборочную среднюю.

-a: -0,1243

-b: -0,1258

+c: -0,1288

-d: -0,1259

16. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,2232; 0,1888; 0,2214; 0,1896; 0,265; 0,1627. Найти выборочную среднюю.

-a: 0,2005

-b: 0,2072

-c: 0,2161

+d: 0,2085

17. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,6133; 0,7759; 0,6386; 0,6918; 0,6468; 0,7391. Найти выборочную среднюю.

+a: 0,6842

-b: 0,6882

-c: 0,6811

-d: 0,6799

18. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,4209; 0,5477; 0,4913; 0,4247; 0,5222; 0,5839. Найти выборочную среднюю.

-a: 0,4923

+b: 0,4985

-c: 0,4921

-d: 0,4929

19. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,9538; 1,1098; 0,9347; 0,9724; 1,2632; 1,1543. Найти выборочную среднюю.

-a: 1,1243

-b: 1,1258

+c: 1,0647

-d: 1,0259

20. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,0598; -0,0662; -0,0042; 0,0435; 0,0967; 0,0838. Найти выборочную среднюю.

-a: 0,0105

-b: 0,0172

-c: 0,0161

+d: 0,0156

21. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,8447; 0,7124; 0,9431; 0,6183; 0,9823; 0,6153. Найти выборочную среднюю.

+a: 0,786

-b: 0,782

-c: 0,711

-d: 0,799

22. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,4953; 0,4977; 0,5033; 0,4726; 0,5266; 0,5037. Найти выборочную среднюю.

-a: 0,4923

+b: 0,4999

-c: 0,4921

-d: 0,4929

23. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,4021; -0,0998; -0,4692; -0,0829; -0,3848; -0,6038. Найти выборочную среднюю.

-a: -0,3547

-b: -0,3487

+c: -0,3404

-d: -0,3421

24. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,4865; 0,4052; 0,539; 0,5869; 0,354; 0,4851. Найти выборочную среднюю.

-a: 0,4705

-b: 0,4472

-c: 0,4861

+d: 0,4761

25. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,7348; 0,7761; 0,6238; 0,9838; 0,728; 0,7737. Найти выборочную среднюю.

+a: 0,77

-b: 0,78

-c: 0,71

-d: 0,79

26. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,518; 0,3269; 0,6991; 0,6851; 0,5274; 0,6477. Найти выборочную среднюю.

-a: 0,5923

+b: 0,5674

-c: 0,5721

-d: 0,5429

27. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,1095; -0,359; -0,5044; -0,1737; -0,1227; -0,4799. Найти выборочную среднюю.

-a: -0,2947

-b: -0,3087

+c: -0,2916

-d: -0,3021

28. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,4888; 0,4034; 0,3259; 0,4123; 0,3793; 0,6322. Найти выборочную среднюю.

-a: 0,4455

-b: 0,4472

-c: 0,4461

+d: 0,4403

29. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,1382; 0,3065; 0,4178; 0,2984; 0,1309; 0,3264. Найти выборочную среднюю.

+a: 0,2697

-b: 0,2678

-c: 0,2671

-d: 0,2679

30. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,4495; 0,5157; 0,514; 0,4852; 0,3125; 0,5336. Найти выборочную среднюю.

-a: 0,4923

+b: 0,4684

-c: 0,4721

-d: 0,4429

31. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,2214; -0,2851; -0,238; -0,1194; -0,214; -0,2948. Найти выборочную среднюю.

-a: -0,2347

-b: -0,2307

+c: -0,2288

-d: -0,2021

32. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,3604; -0,395; -0,3397; -0,3729; -0,3439; -0,3227. Найти выборочную среднюю.

-a: -0,3555

-b: -0,3472

-c: -0,3461

+d: -0,3558

33. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,3319; 0,4173; 0,339; 0,2417; 0,3027; 0,4787. Найти выборочную среднюю.

+a: 0,3519

-b: 0,3678

-c: 0,3571

-d: 0,3579

34. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,9267; 0,8961; 0,8828; 1,0042; 0,9145; 0,8942. Найти выборочную среднюю.

-a: 0,9123

+b: 0,9198

-c: 0,9171

-d: 0,9129

35. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,4254; -0,3936; -0,0472; -0,2703; -0,5544; -0,1623. Найти выборочную среднюю.

-a: -0,3047

-b: -0,3007

+c: -0,3089

-d: -0,3021

36. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,3176; -0,2795; -0,2567; -0,1596; -0,2434; -0,3585. Найти выборочную среднюю.

-a: -0,2655

-b: -0,2672

-c: -0,2661

+d: -0,2692

37. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,7169; 0,3905; 0,6771; 0,7361; 0,6444; 0,6764. Найти выборочную среднюю.

+a: 0,6402

-b: 0,6478

-c: 0,6471

-d: 0,6409

38. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,3202; -0,1685; -0,308; -0,4623; -0,3387; -0,3787. Найти выборочную среднюю.

-a: -0,3291

+b: -0,3294

-c: -0,3288

-d: -0,3277

39. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,0116; -0,0819; -0,0906; -0,0289; -0,0603; -0,0933. Найти выборочную среднюю.

-a: -0,3047

-b: -0,3007

+c: -0,0572

-d: -0,3021

40. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,5267; 0,5025; 0,6446; 0,6141; 0,5232; 0,411. Найти выборочную среднюю.

-a: 0,555

-b: 0,572

-c: 0,561

+d: 0,537

41. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,3574; 0,2996; 0,1617; 0,2726; 0,1925; 0,2284. Найти выборочную среднюю.

+a: 0,252

-b: 0,258

-c: 0,257

-d: 0,259

42. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,0587; 0,1099; 0,1061; 0,1794; 0,0971; -0,0071. Найти выборочную среднюю.

-a: 0,0991

+b: 0,0907

-c: 0,0897

-d: 0,0977

43. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,6057; 0,6074; 0,3934; 0,5555; 0,3747; 0,4527. Найти выборочную среднюю.

-a: 0,4987

-b: 0,4907

+c: 0,4982

-d: 0,4921

44. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,1857; 0,3331; 0,5448; 0,4433; 0,4162; 0,2359. Найти выборочную среднюю.

-a: 0,3555

-b: 0,3572

-c: 0,3561

+d: 0,3598

45. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,3843; -0,0353; -0,2999; -0,176; -0,141; -0,2529. Найти выборочную среднюю.

+a: -0,2149

-b: -0,2158

-c: -0,2157

-d: -0,2159

46. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,4089; -0,2698; -0,2835; -0,3999; -0,4914; -0,3496. Найти выборочную среднюю.

-a: -0,3691

+b: -0,3672

-c: -0,3697

-d: -0,3677

47. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,0907; -0,1961; 0,2716; 0,0066; 0,2288; 0,1765. Найти выборочную среднюю.

-a: 0,0987

-b: 0,0907

+c: 0,0963

-d: 0,0921

48. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,1295; -0,2921; -0,2376; -0,2272; -0,3811; -0,3025. Найти выборочную среднюю.

-a: -0,2655

-b: -0,2672

-c: -0,2611

+d: -0,2617

49. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,94; 0,7661; 0,7478; 0,6698; 0,8385; 0,7818. Найти выборочную среднюю.

+a: 0,7907

-b: 0,7958

-c: 0,7957

-d: 0,7909

50. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,1007; 0,0442; 0,0768; -0,0772; 0,0888; -0,1985. Найти выборочную среднюю.

-a: -0,0291

+b: -0,0277

-c: -0,0297

-d: -0,0287

51. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,2368; -0,1204; -0,0612; 0,0994; 0,055; -0,0955. Найти выборочную среднюю.

-a: 0,018

-b: 0,017

+c: 0,019

-d: 0,016

52. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,0821; -0,0014; 0,1327; 0,1115; 0,1648; 0,0665. Найти выборочную среднюю.

-a: 0,0921

-b: 0,0924

-c: 0,0926

+d: 0,0927

53. Дана выборка из нормального распределения, дисперсия которого неизвестна:

-0,343; -0,4149; -0,4238; -0,2922; -0,2681; -0,3191. Найти выборочную среднюю.

+a: -0,3435

-b: -0,3458

-c: -0,3457

-d: -0,3409

54. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,5636; 0,5704; 0,5588; 0,6175; 0,5081; 0,5637. Найти выборочную среднюю.

-a: 0,5691

+b: 0,5637

-c: 0,5697

-d: 0,5647

55. Дана выборка из нормального распределения, дисперсия которого неизвестна:

0,6517; 0,2752; 0,3277; 0,5321; 0,6613; 0,4804. Найти выборочную среднюю.

-a: 0,4887

-b: 0,4877

+c: 0,4881

-d: 0,4886

56. Из генеральной совокупности извлечена выборка объёма :

	1	2	3	4	5	6
	25	24	23	22	21

Тогда относительная частота варианты равна…

-a: 0,375

-b: 0,575

+c: 0,425

-d: 0,10

57. Из генеральной совокупности извлечена выборка объёма :

	1	2	3	4	5	6
	25	20	27	22	21

Тогда относительная частота варианты равна…

-a: 0,375

-b: 0,575

+c: 0,425

-d: 0,10

58. Статистическое распределение выборки имеет вид:

	3	7	8	9
	2	4	6	10

Тогда объём выборки равен…

+a: 22

-b: 49

-c: 27

-d: 4

59. Статистическое распределение выборки имеет вид:

	3	7	9	12
	2	4	6	12

Тогда объём выборки равен…

+a: 24

-b: 49

-c: 27

-d: 4

60. Из генеральной совокупности извлечена выборка объёма :

	4	6	8	10	12	14
	10	15	20	25	30

Тогда значение равно…

-a: 110

-b: 20

-c: 35

+d: 10

61. Из генеральной совокупности извлечена выборка объёма :

	4	6	8	10	12	14
	10	19	16	20	35

Тогда значение равно…

-a: 110

-b: 20

-c: 35

+d: 10

62. Из генеральной совокупности извлечена выборка объёма :

	1	2	3	4	5	6
	22	16	14	12	10

Тогда относительная частота варианты равна…

-a: 0,28

-b: 0,74

+c: 0,26

-d: 0,24

63. Из генеральной совокупности извлечена выборка объёма :

	1	2	3	4	5	6
	22	16	14		10	12

Тогда относительная частота варианты равна…

-a: 0,28

-b: 0,74

+c: 0,26

-d: 0,24

64. Из генеральной совокупности извлечена выборка объёма :

2

4

Тогда относительная частота варианты равна…

+a: 0,375

-b: 0,45

-c: 0,385

-d: 0,75

65. Из генеральной совокупности извлечена выборка объёма :

	4	6	8	10	12	14
	10	15	20	25	30

Тогда значение равно…

-a: 120

-b: 30

-c: 35

+d: 20

66. Из генеральной совокупности извлечена выборка объёма :

2

4

Тогда варианта равна…

+a: 11

-b: 12

-c: 67

-d: 9

67. Из генеральной совокупности извлечена выборка объёма , гистограмма частот которой имеет вид:

a

13

10

7

0

3

12

16

20

4

8

Тогда значение a равно…

+a: 17

-b: 67

-c: 18

-d: 33

68. Статистическое распределение выборки имеет вид:

	3	7	8	9
	3	4	5	10

Тогда объём выборки равен…

+a: 22

-b: 49

-c: 27

-d: 4

69. Из генеральной совокупности извлечена выборка объёма :

2

4

Тогда относительная частота варианты равна…

+a: 0,375

-b: 0,45

-c: 0,385

-d: 0,75

70. Из генеральной совокупности извлечена выборка объёма :

2

4

Тогда варианта равна…

+a: 22

-b: 12

-c: 134

-d: 9

71. Из генеральной совокупности извлечена выборка объёма , гистограмма частот которой имеет вид:

a

13

10

7

0

3

9

12

15

3

6

Тогда значение a равно…

+a: 16

-b: 48

-c: 18

-d: 33

72. Статистическое распределение выборки имеет вид:

	0-1,5	1,5-3	3-4,5	4,5-6	6-7,5
	10	32	60	28	20

Тогда объём выборки равен…

-a: 140

+b: 150

-c: 225

-d: 100

Решение: объём выборки вычисляется по формуле , где - сумма частот частичного интервала . Тогда n=10+32+60+28+20=150.

73. Из генеральной совокупности извлечена выборка объёма n=100:

	3	4	5	6	7
	7		45	21	2

Тогда относительная частота варианты равна…

-a: 0,75

-b: 0,24

+c: 0,25

-d: 0,04

Решение: относительная частота вычисляется по формуле , где - частота варианты , а - объём выборки. Предварительно вычислим частоту варианты х=3 как n₂=100-7-45-21-2=25. Тогда

74. Из генеральной совокупности извлечена выборка объёма n=100, полигон частот которой имеет вид:

Тогда статистическое определение выборки можно определить как…

-a

	4	8	12	16	20
	0,09	0,13	0,17	0,28	0,33

+b:

	4	8	12	16	20
	0,17	0,33	0,28	0,09	0,13

-c:

	4	8	12	16	20
	0,33	0,28	0,17	0,13	0,09

-d:

	4	8	12	16	20
	0,07	0,33	0,28	0,09	0,13

Решение: Предварительно вычислим частоту варианты х=4 как n₁=100-33-28-13-9=17. Так как относительные частоты вычисляются по формуле , где - частота варианты , а - объём выборки, то статистическое распределение данной выборки может иметь вид:

	4	8	12	16	20
	0,17	0,33	0,28	0,09	0,13

75. Из генеральной совокупности извлечена выборка объёма n=100, полигон относительных частот которой имеет вид:

Тогда число вариант в выборке равно…

-a: 63

-b: 100

+c: 37

-d: 36

Решение: Предварительно вычислим относительную частоту варианты как

w₁=1-0,25-0,21-0,12-0,05=0,37. Тогда из определения относительной частоты , получаем, что

76. Статистическое распределение выборки имеет вид:

	2	4	6	8
	0,05	0,15	0,25

Тогда значение относительной частоты равно…

-a: 0,35

-b: 0,45

-c: 0,65

+d: 0,55

77. Из генеральной совокупности извлечена выборка объёма n=100, гистограмма относительных частот которой имеет вид:

Тогда статистическое определение выборки можно определить как…

-a

	0-2	2-4	4-6	6-8
	4	11	20	15

+b:

	0-2	2-4	4-6	6-8
	8	22	40	30

-c:

	0-2	2-4	4-6	6-8
	8	22	30	40

-d:

	0-2	2-4	4-6	6-8
	40	30	22	8

Решение: из определения относительной частоты , что . Тогда с учётом того, что h=2 частоты можно вычислить как , т.е. статистическое распределение выборки может иметь вид:

	0-2	2-4	4-6	6-8
	8	22	40	30

78. Из генеральной совокупности Х извлечена выборка объёма n=50:

	5	6	7	8
	24	14	7	5

Тогда её эмпирическая функция распределения вероятностей имеет вид:

-a:

-b:

+c:

-d: