Особенности обучения решению задач по программе Н.Б. Истоминой

Несколько иной подход в формировании у детей умения решать текстовые задачи предлагает доктор педагогических наук, профессор Н.Б. Истомина.

Постараемся разобраться, в чем суть этого подхода и в чем он отличается от традиционной методики обучения решению задач.

Исследуя методику обучения решению задач, которая находит отражение в практике начального обучения математике, Н.Б. Истомина обнаружила два противоречия

Первое из них, связанное с функцией задач как средства формирования у учащихся математических представлений, заключается в том, что с одной стороны, решение задачи должно сводиться к выбору арифметического действия (запись выражения), выполнение которого (вычисление значения выражения) позволяет ответить на вопрос, поставленный в задаче. С другой стороны, представления детей о смысле арифметических действий формируется в процессе решения простых задач. Суть противоречия сводится к тому, что дети должны выбрать арифметические действия, не имея представлений о том, что это такое, а опираясь на жизненный опыт. Снять это противоречие можно только через показ образца решения каждого типа задачи с последующим его закреплением.

Второе противоречие заключается в том, что с одной стороны, детей знакомят со структурой задачи (условие, вопрос, известное, неизвестное), а с другой — для формирования умения анализировать задачу с точки зрения ее структуры используют однообразные текстовые конструкции, которые всегда начинаются с условия, содержащего данные или известные, затем всегда следует вопрос и то, о чем спрашивается в вопросе - это неизвестное. В связи с этим у учащихся не только не формируется умение анализировать текст задачи, но и не возникает даже потребности в этом. В результате, используя для решения простой задачи житейские представления и ориентируясь на слова-действия «подарили - взяли», «было - осталось» и так далее большинство учащихся узнают задачу и вспоминают, каким действием она решается.

Рассмотрим другой подход к обучению решению задач, который предлагает Н.Б. Истомина. Его основная идея заключается в том, что смысл арифметических действий осознается учащимися до решения задач (7, 25). Сторонником этой точки зрения является прогрессивный русский методист Э.А. Эрн, который считал, что у ученика сначала должно быть сформировано понятие об арифметическом действии и лишь затем умение выбрать то или иное действие для решения данной простой задачи. Психолог Н.А. Меченская также рассматривала выбор арифметического действия как новую умственную операцию, суть которой сводится к переводу конкретной ситуации , описанной в задаче, в план арифметических операций. Безусловно, для выполнения операций в умственном плане ученик должен овладеть ими на предметном уровне. В связи с этим знакомство учащихся с текстовой задачей отодвигается на более поздний период, которому предшествует большая подготовительная работа, целью которой является формирование у младших школьников:

1. навыков чтения;

2. представлений о тех математических понятиях и отношениях, которые обеспечивают сознательную математизацию сюжетов, представленных в текстовых задачах;

3. приемов умственных действий (логические приемы мышления - анализ, синтез, сравнение, аналогия, обобщение), которые

решения ^о

При этом существенным является не отработка умения решать определенные типы (виды) текстовых задач, а приобретение учащимися опыта в семантическом и математическом анализе различных текстовых конструкций задач и формирование умения представлять их в виде схематической и символической моделей. Средством организации этой деятельности могут быть специальные обучающие задания, включающие методические приемы сравнения, выбора, преобразования, конструирования.

Ознакомление с понятием «Задача».

Рассмотрим задания, которые предлагаются детям в развивающей системе Н.Б. Истоминой и используемые методические приемы. Сравнение текстов задач.

Задача: 1. На одном проводе сидели ласточки, а на другом 7 воробьев. Сколько всего сидело птиц на проводах ?

2. На одном проводе сидело 9 ласточек, а на другом 7 воробьев. Сколько всего птиц сидело на проводах ?

Чем похожи тексты задач ? Чем отличаются ? Какую задачу ты можешь решить? Какую не можешь ? Почему ?

- Подумай ! Будут ли эти тексты задачи задачами ?

1. На одной тарелке 3 огурца, на другой - 4. Сколько помидоров на тарелках ?

2. на одной клумбе росло 5 тюльпанов и 3 розы. Сколько тюльпанов росло на клумбе ?

- Сравни тексты задач. Чем они похожи ? Чем отличаются ? Можно ли утверждать, что решение задач будет одинаковым ?

1. Возле дома росло 7 яблонь и 3 вишни. Сколько фруктовых деревьев росло возле дома ?

2. Возле дома росло 7 яблонь, 3 вишни, 2 березы. Сколько фруктовых деревьев росло возле дома ?

- Сравни тексты задач. Чем они похожи ? Чем отличаются ?

1. Из бочки взяли 10 ведер воды. Сколько ведер воды взяли из бочки ?

2. В бочке 40 ведер воды. Сколько ведер воды осталось в бочке ?

(Использованы тексты задач с недостающими и лишними данными, противоречивым условием и вопросом, с вопросом, в котором спрашивается о том, что уже известно).

Обучение решению задач.

Подготовительная работа к решению задач.

Центральным звеном в умении решать задачи, которым должны овладеть учащиеся, является усвоение связей между данными и искомым.

На первой ступени учитель ведет подготовку к решению задач рассматриваемого вида. На этой ступени ученики должны усвоить связи, на основе которых они будут выбирать действия при решении таких задач. Подготовительная работа к решению задач того или иного вида зависит от того, на какую связь между данными и искомым надо опираться при выборе арифметических действий. В соответствии с этим проводятся специальные упражнения.

1. Во многих случаях для решения задач выполняются операции над множествами. Ознакомлению с решением большинства простых задач должны предшествовать упражнения по оперированию множествами, причем элементами множеств должны быть конкретные предметы. Например, до введения простых задач па нахождение суммы предлагаются упражнения на объединение множеств.

- Достаньте картинки, на которых нарисованы зайчики. На лужайке прыгали 4 зайчика. К ним прибежали еще 3 зайчика (выкладывают еще 3 картинки). Сколько всего стало зайчиков? (Дети считают картинки). Мы к 4 прибавили 3 (показывает на картинки) и получили 7.

Подготовкой к решению задач на вычитание будет удаление части множества, на умножение - объединение равночисленных множеств, на деление - разбиение множества на ряд равночисленных множеств.

С помощью операций над множествами раскрывается смысл выражений «больше на», «меньше на», «больше в несколько раз», «меньше в несколько раз», что является подготовкой для введения задач, связанных с понятием разности и кратного отношения.

2. Большинство арифметических задач связаны с величинами, поэтому до включения в ту или иную задачу новой величины надо ознакомить детей с этой величиной. При этом детям полезно для дальнейшей работы записывать в отдельные тетради значения некоторых величин, цены на отдельные товары, скорости различных видов транспорта, расстояние между городами или поселками.

3. Выбор арифметических действий при решении многих задач выполняется на основе связей, существующих между этими величинами. Чтобы учащиеся при выборе действий использовали и осознавали эти связи, надо раскрыть связи между величинами путем решения задач на основе их конкретного смысла. Например, надо решить задачу: «Купили 3 открытки по 4 коп. за штуку. Сколько уплатили денег?» Для решения этой задачи используется знание связи: если известны цепа товара и его количество, то можно найти стоимость действием умножение.

Чтобы учащиеся усвоили ту или иную связь, следует организовать целенаправленные наблюдения. Так, для раскрытия связи между ценой, количеством и стоимостью можно провести экскурсию в магазин, где учащиеся познакомятся с ценой, запишут цены на некоторые товары в своих справочниках и пронаблюдают процесс купли-продажи Далее на уроке они составят ряд простых задач па нахождение стоимости по известным цене и количеству, затем решат их, опираясь на знание конкретного смысла действия умножения. Рассмотрев решения, учащиеся заметят, что если известны цена и количество, то стоимость находят действием умножения. В дальнейшем это знание учащиеся будут использовать при решении задач как простых, так и составных.

4. Решение составных задач сводится к решению ряда простых, поэтому подготовкой к решению составных задач будет обучение решению соответствующих простых задач.

При работе над каждым отдельным видом задач требуется своя специальная подготовительная работа, о чем подробнее говорится в методике обучения решению задач каждого вида.

Ознакомление с решением задач.

Предусмотрев соответствующую подготовительную работу, можно перейти к ознакомлению детей с решением задач рассматриваемого вида.

Ознакомиться с содержанием задачи значит, прочитав се, представить жизненную ситуацию отраженную в задаче.

Читая задачу дети должны представлять ту жизненную ситуацию, которая отражена в задаче. С этой целью полезно после чтения предлагать им представить себе то, о чем говорится в задаче и рассказать, как они представили.

Полное решение задачи состоит из анализа условия: плана выполнения арифметических действий и ответа.

К решению задачи также относят проверку и исследование пригодности полученного ответа.

Обучение решению типовых задач.

Составная задача включает в себя ряд простых задач, связанных между собою так, что искомые одних задач служат данными других. Решение составной задачи сводится к расчленению ее на ряд простых задач и к последующему их решению. Для решения составной задачи необходимо установить не одну связь, а несколько, в соответствии с которыми выбрать арифметические действия.

Классификация типовых задач.

1. Задачи на нахождение 4-го пропорционального

№	Величины			ЗАДАЧИ
п/п	цена	количество	стоимость
1.	Постоян.	Даны 2 значения.	Дано 1 знач. Другое искомое
2.	Постоян.	Дано 1 знач. Другое искомое	Даны 2 значения.
3.	Даны 2 значения.	Постоянная	Дано 1 знач. Другое искомое
4.	Дано 1 знач. Другое искомое.	Постоянная.	Даны 2 значения.
5.	Даны 2 значения.	Дано 1 знач. Другое искомое	Постоянная.
6.	Дано 1 знач. Другое искомое.	Даны 2 значения.	Постоянная

2. Задачи на пропорциональное деление

№ п/п	Величины			ЗАДАЧИ
	ценя	количество	стоимость
1.	Постоян.	Даны 2 значения.	Дана сумма. Найти слагаемые
2.	Постоян.	Дана сумма. Найти слагаемые	Даны 2 значения.
3.	Даны 2 значения.	постоянная	Дана сумма. Найти слагаемые
4	Дана сумма. Найти слагаемые	постоянная	Даны 2 значения.
5.	Даны 2 значения.	Дана сумма. Найти слагаемые	постоянная
6.	Дана сумма. Найти слагаемые	Даны 2 значения.	постоянная

В начальных классах рассматриваются задачи только первых 4-х видов.

1. Задачи на нахождение неизвестного по двум разностям

№ п/п		Величины					ЗАДАЧИ
		цена	количество		стоимость
1.		постоянная	Даны 2 значения.		Дана разность значений. Найти каждое значение.
2.	Даны 2 значения.		Дана разность значений. Найти каждое значение.	Даны 2: 31.
3.	Даны 2 значения.		постоянная	Дана разность значений. Найти каждое значение.
4.	Дана разность значений. Найти каждое значение.		постоянная	Даны 2 значения.
5.	Даны 2 значения.		Дана разность значений. Найти каждое значение.	постоянная
6.	Дана разность значений. Найти каждое значение.		Даны 2 значения.	постоянная

В начальных классах рассматриваются первые два вида задач.

К типовым задачам относят так же задачи на движение и на нахождение доли числа и числа по его доле.

1. Анализ текста задачи.

В типовой задаче необходимо выделить языковые фрагменты, которые являются ключевыми для построения: математической модели:

• словесные описания величин;

важным моментов является выделение из условия пропорциональных величин, их словесное обозначение - цена, количество, стоимость; масса одно­го предмета, количество предметов, общая масса; выработка в единицу времени, время работы, общая выработка и другие;

• в тексте задач с пропорциональными величинами присутствуют явные или скрытые смыслы, которые относятся к разряду кванторных. Языковым по­казателем кванторов являются слова - все, каждый, всякий, любой, существует, найдется — слова показывают постоянную величину;

• важным моментом для построения математической модели задачи явля­ется показатель операций и отношений, которые помогают при составлении краткой записи и определения типа задачи.

Функция слова «всего» - указать, что дана сумма, соответствующая значению одной переменной величины, слагаемые этой суммы являются искомыми. Тип - на пропорциональное деление

Функция слова «больше» (меньше) показать, что дана разность значений переменной величины, а сами значения этой переменной являются искомые. Тип - на нахождение неизвестного по 2 разностям

2. Составление краткой записи.

В зависимости от задачи более удобен тот или другой вид краткой записи - таблица, схема, чертеж.

В таблице последовательность записи величины должна быть единой.

• цена; количество, стоимость

• скорость, время, расстояние,

• урожайность, площадь участка, урожай,

• выработка в единицу времени, время работы, общая выработка,

• емкость одного сосуда, количество сосудов, общая емкость и т. д.

Например, задача № 654 с. 118 (.3 о. /1 -3)

Масса 1 мешка	Кол-во мешков	Общая масса
одинаковая	4	? 480 кг ? ?
	6

Также задачу можно схематически представить другими способами.

Например:

схематическая иллюстрация

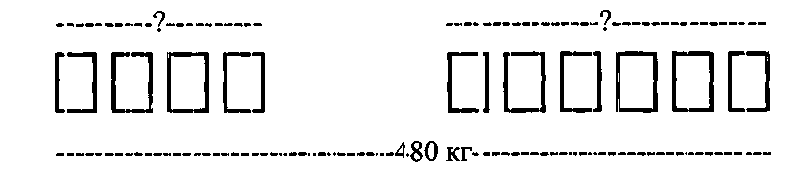
С помощью чертежа.

Этапы обучения учащихся решению задач с пропорциональными величинами.

1 этап. Ознакомление с величинами и зависимостью между величинами в процессе решения простых задач.

Заполните таблицу и составьте 3 задачи с величинами.

Цена	количество	стоимость
?	а	в
а	?	в
в	а	?

Емкость одного сосуда	Количество сосудов	Общая емкость
?	в	а
в	?	а
в	а	?

Выработка в единицу времени	Время работы	Общая выработка
?
	?
		?