10.5. Решение уравнения движения ротора генератора. Метод последовательных интервалов

Уравнение движения ротора нелинейно и не может быть решено в общем виде. Исключением является полный сброс мощности в аварийном режиме, т.е. Р_{ав. max} = 0, рассмотренный выше. Уравнеие (9.7) решается методами численного интегрирования [14]. Одним из них является метод последовательных интервалов, иллюстрирующий физическую картину протекания процесса. В соответствии с этим методом весь процесс качания ротора генератора разбивается на ряд интервалов времени t и для каждого из : них последовательно вычисляется приращение угла . В момент КЗ отдаваемая генератором мощность падает и возникает некото­рый избыток мощности Р(о). Для малого интервала t можно допустить, что избыток мощности в течение этого интервала остается неизменным. Интегрируя выражение (9.7), получаем в конце пер­вого интервала

Относительная скорость ротора в момент КЗ равна нулю (с₁ = 0), и поэтому относительная скорость ротора в конце первого интерва­ла равна V₍₁₎. При t = 0 угол  = о, поэтому с₂ = ₀. Ускорение а₀ может быть вычислено из (9.4): а₍₁₎ = Р(о) / Т_j отсюда следует

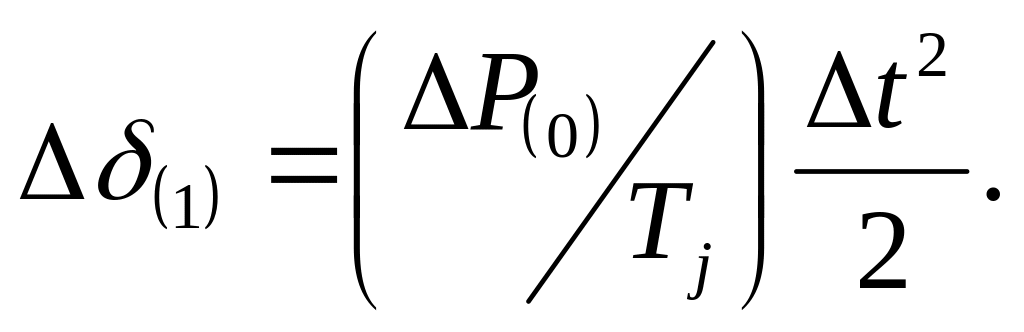
Здесь угол и время представлены в радианах. В практических рас­четах угол выражают в градусах, а время - в секундах:

, (10.8)

t_(с)=t_(рад)/₍₀₎ (10.9)

Используя (10.8) и (10.9) и учитывая, что T_j(с) = Т_j(рад)/₀ , полу­чаем

где

(10.10)

Ускорение, создаваемое во втором интервале, пропорциональ­но избытку мощности в конце первого интервала . При вычис­лении приращения угла в течение второго интервала необходимо учесть то, что кроме действующего в этом интервале ускорения ₍₁₎ ротор уже имеет в начале интервала скорость V₍₁₎:

(10.11)

где Р₍₁₎ = p₍₀₎ - P_max sin (₁).

Значение скорости V₁ - неточное, так как ускорение ₍₀₎ не яв­ляется постоянным в течение первого интервала времени. Более точное значение скорости можно получить, если предположить, что на первом интервале действует среднее ускорение:

_(0)ср = (₍₀₎ + ₍₁₎)/2.

Тогда относительная скорость будет выражена формулой

V₍₁₎=_(0)cpf = .

Подставляя это уравнение в (10.11), получаем

или ₍₂₎ =_(i) + К.Р₍₁₎.. Прира­щение угла на последующих ин-тервалах рассчитывается анало­гично: _(n) =_{(n - i)} + К.Р_{(n - 1)}.. Ес­ли в начале некоторого K-интервала происходит отключение КЗ, то избыток мощности внезап­но изменяется от некоторой ве­личины .Р’_{(K - 1)}.. (рис. 10.6) до .Р’’_{(K - 1)}., что соответствует пере ходу с характеристики 1 на 2. Приращение угла на первом интервале после отключения КЗ определится как

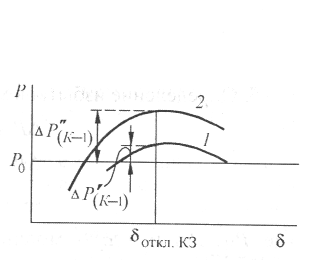
Рис. 10.6. К определению избытком мощности при переходе от одного режима (характеристика /) к дру­гому (характеристика 2)

(10,12)

Расчет методом последовательных интервалов ведется до тех пор, пока угол  не начнет уменьшаться либо не будет ясно, что угол неограниченно растет, т.е. устойчивость машины нарушается.