10.3. Предельный угол отключения кз

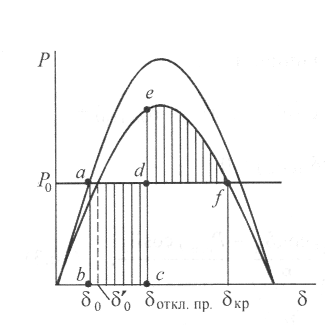
Из рис. 10.3 можно найти предельное значение угла отключе­ния КЗ, при котором устойчивая работа системы сохраняется. Оно определяется равенством площади ускорения f_abcd и возможной площади торможения f_defm. Приравнивая к нулю сумму этих пло­щадей, получаем аналитическое выражение для предельного угла отключения КЗ:

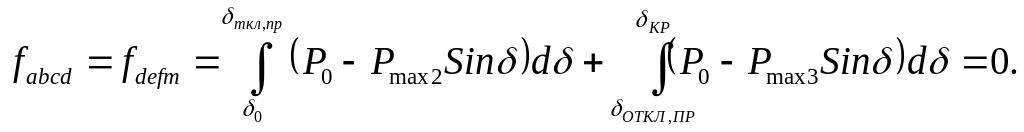
Раскрывая определенные интегралы, запишем

Ро(ткл.пр - ₀) + Pmax2(COS_OTKJ1пр - COS₀) + Ро(кр - откл.пр) + Pmах(COS_кр - COS_OTKJ1пр) = 0.

Откуда

(10.3)

(все углы выражены в радианах).

Однако для практических целей знания угла _{откл пр} недостаточно. При выборе выключателей и расчете релейной защиты необходимо знать не угол, а период времени, в течение которого ротор успевает достигнуть этого угла, т.е. предельно допустимое время отключения КЗ. Это время может быть определено решением уравнения движения ротора генератора известными методами ре­шения дифференциальных уравнений (например, методом Рунге - Кутта 4-го порядка или методами последовательных интервалов).

10.4. Анализ трехфазного кз графическим методом

При трехфазном КЗ в точке К1 взаимное сопротивление схемы становится бесконечно большим, так как сопротивление шунта КЗ

. При этом характеристика мощности аварийного режима совпадает с осью абсцисс (рис. 10.4). Ротор генератора начинает свое относительное движение под действием избыточного момента, равного механическому моменту турбины. Дифференциальное уравнение движения ротора при этом принимает вид

(10.4) Это уравнение линейно, и нетрудно получить его решение. Пе­репишем (10.4) в следующем виде:

откуда, взяв интеграл от левой и правой частей, получим

(10.5)

При t= 0 относительная ско­рость ротора  = 0 и, следователь­но, С1 = 0. Проинтегрировав еще раз (10.5), имеем

l

Рис. 10.4. Трехфазное КЗ в начале линии

Постоянная интегрирования с₂ определяется из условий  = ₀, с₂ = ₀ при t = 0. Окончательно зависимость угла от времени будет иметь вид

(10.6)

Возрастание угла происходит по квадратической параболе, а время, отвечающее какому-либо значению угла , находится из уравнения (10.6):

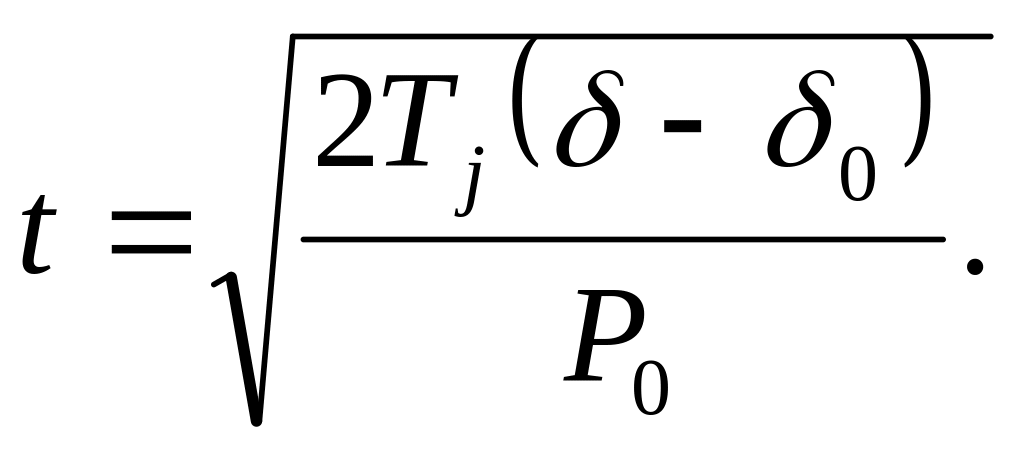(10.7)

Предельный угол отключения трехфазного КЗ может быть оп­ределен из выражения (10.3), упрощенного условием Р_max2 = 0:

Предельное время отключения при трехфазном КЗ определится из выражения (10.7):

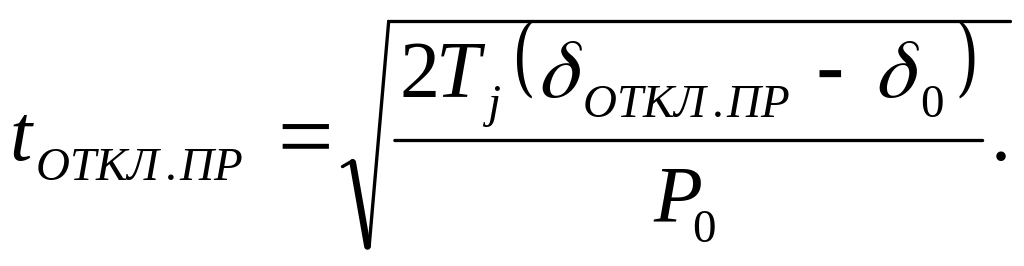
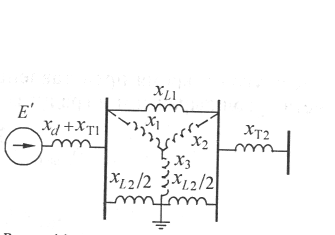
Когда трехфазное КЗ происходит не в начале линии (а, напри­мер, в ее середине), то условия нахождения взаимного сопротивления изменяются. Оно уже имеет конечное значение и определяется из схемы, показанной на рис. 10.5. Преобразовав треугольник из сопротивлений линий х_L1, x_L2/2 в звезду х₁, х₂, х₃, получим схему связи генератора с системой, подобную схеме для несимметричного КЗ, изображенную на рис. 10.2, б.

Гис. 10.5. Схема замещения

и ее преобразование при

трехфазном КЗ в середине линии

Динамический переход в этом случае аналогичен переходу при I несимметричном КЗ.