Лекция 9
Влияние эффекта «состязаний» или «гонок» на работу триггеров.
Явление неодновременности изменения выходных сигналов логических элементов при одновременном изменении их входных сигналов называют состязанием ЛЭ. Состязание, приводящее к возникновению ложных коротких импульсов называют критическим.
Если в комбинационных схемах учитывать время переходного процесса и снимать результат только по окончании переходных процессов, то на достоверности результата эффект состязаний не отражается. Наличие же ложных импульсов может существенно изменить работу автоматов. Поэтому при формировании управляющих сигналов в автоматах одним из основных требований является исключение критических состязаний.
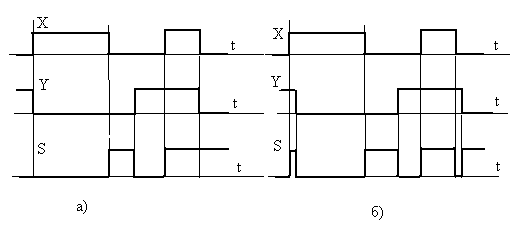
Пример возникновения ложных импульсов
при формировании сигнала
для
идеального случая синхронного изменения
сигналов (см. а) и при возникновении
небольшого смещения их, вызванного
задержкой на реальных элементах (см. б)
П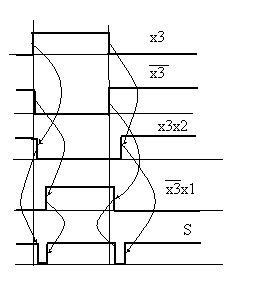
ри
разработке устройств, свободных от
критических состязаний, необходимо
стремиться к тому, чтобы в каждый момент
времени возможно было изменение только
одного входного сигнала. При минимизации
логических функций с помощью матриц
Карно для исключения критических
состязаний необходимо, чтобы все соседние
единичные клетки покрывались хотя бы
одним общим кубом. Пример,
при
единичных значениях х1, х2 и изменении
х3 из за разного времени перехода сигнала
с 0 в 1 и с 1 в 0 (для ТТЛ первое больше
второго) имеем на каждое изменение х3
ложный импульс (см. рис.). По диаграмме
Вейча объединяя все соседние единицы,
получаем
.
При единичных х1 и х2 получаем
и импульсы отсутствуют.
В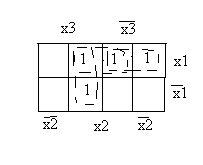
озникновение
ложных импульсов проверяют путем
событийного моделирования работы
устройства. При таком моделировании
задают время задержки перехода выхода
ИС из нулевого в единичное состояние и
из единичного в нулевое в соответствии
с паспортными данными ИС и моделируют
изменение выходного сигнала при изменении
входных по логическим функциям с учетом
времени задержки изменения состояния
выходов элементов.
Q+ |
L |
D |
Q |
0 1 0 1 0 0 1 1 |
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
И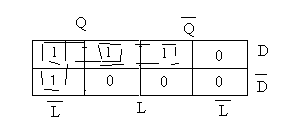
меет
два входа: D – (Data)
информационный и L –
(Load) загрузка. При L=1
выход триггера принимает значение D,
причем, при изменении D
выход также будет изменяться. При L=0
выход сохраняется. Таблица истинности
и матрица Карно представлены на рисунках.
Логическая функция для схемы, свободной от состязаний, имеет вид:
.
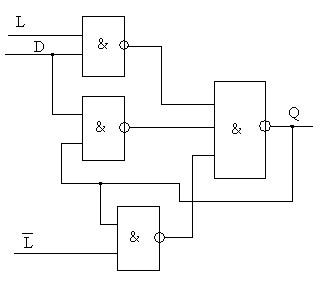
В базисе И-НЕ
. Полученный триггер называют триггером
Эрла. Он имеет максимальное быстродействие
и широко используется в асинхронных
(потенциальных) регистрах.
Исходную логическую функцию Q+ можно также преобразовать следующим образом:
Последней функции соответствует схема
которая имеет меньшее быстродействие
по с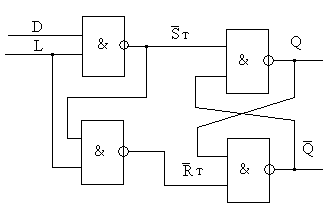
равнению
с триггером Эрла, но не требует инверсии
L, имеет прямой и инверсный
выходы, и меньше элементов.
Как видно по схеме, при L=1 триггер становится комбинационной схемой для D (“прозрачным» для сигнала D). При переходе L c единичного на нулевой уровень на выходе Q будет зафиксировано то значение D, которое он имел в момент перехода.
(Лучше дать через RS – триггер ??. См. уже готовую таблицу истинности)