Лекция 8 Последовательностные схемы или дискретные автоматы с памятью

Сигнал на выходе автомата с памятью (в дальнейшем – автомата) в каждый момент времени определяется не только комбинацией входных сигналов в данный момент времени но и состоянием самого автомата в этот момент времени. Это состояние является результатом воздействия входных сигналов в предыдущие моменты времени. Выход автомата определяется последовательностью изменения входных сигналов. Т.е. автоматы - это устройства с памятью. В отличие от аналоговых устройств, влияние состояния автомата на его выход не является следствием инерционности устройства, а результатом фиксации состояния в памяти автомата и оно может сохраняться там очень долго.

Математическое описание автоматов производится с помощью уравнений состояния.

Пусть в момент времени t состояние будет Q(t) и входной сигнал X(t). Тогда состояние в момент определяется уравнением

, где F - оператор перехода.

Автоматы в зависимости от их свойств условно разделяют классы:

По условиям формирования выходов:

- выход определяется только состоянием автомата т. е. - автомат Мура;

- выход определяется состоянием автомата и входом т. е. - автомат Мили.

По условиям изменения состояния:

- изменение происходит с изменением входных сигналов – не тактируемые или асинхронные;

- изменение происходит с изменением тактового (стробирующего) сигнала – тактируемые или синхронные, , где С(t) – тактовый импульсный сигнал.

Тактовый сигнал обычно имеет постоянный период Т (постоянную частоту), который для обеспечения достоверности фиксируемой информации (состояний) должен быть больше времени переходных процессов по изменению состояния автомата. При постоянном Т состояния в моменты времени Т, 2Т, 3Т и т.д. могут просто индексировать номером периода: .

Помимо операторов перехода дискретные автоматы могут быть описаны с помощью таблиц и графов состояния. Автоматы Мили задаются таблицами перехода состояний и таблицами выходов, аналогичными таблицам истинности для комбинационных схем или таблицам переходов, автоматы Мура – только таблицами переходов. В таблицах переходов в первой строке записывают все возможные состояния автомата в момент времени t, в первой колонке – все возможные комбинации входных сигналов в момент времени t. В клетках внутренней части таблицы заносят состояния, получающиеся в момент t+ Δt при воздействии соответствующих входных сигналов на автомат, находящийся в соответствующем состоянии.

Как на графах, так и в таблицах состояния и сигналы могут быть представлены либо в символьном виде, либо в двоичных одно- или многоразрядных кодах.

Состояния Входы	Q1(t)	…	Qn(t)
X1(t)	Q1,1(t+Δt)	…	Q1,n(t+Δt)
…	…	…	…
Xm(t)	Qm,1(t+Δt)	…	Qm,n(t+Δt)

Используют также таблицы истинности, аналогичные комбинационным схемам, но в отличие от них, в качестве входов рассматриваются также выходы автомата.

Изображение состояний автомата с помощью графов.

Н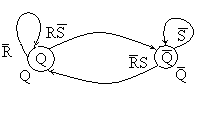 а графе переходов состояния автомата изображаются окружностями или вершинами графа, переходы между состояниями – направленными дугами, называемыми ветвями или ребрами графа. В вершинах графа указывается состояние автомата, на дугах ветвей – сигналы, вызывающие переход из состояния в котором начинается ветвь в состояние, в котором она заканчивается. Направление перехода указывается стрелкой. Выходной сигнал для автомата Мили записывается в конце ветви перехода, входной, вызвавший соответствующий переход, записывают в начале ветви. Выходной сигнал на графе автомата Мура указывают возле соответствующей вершины.

Структурная схема автоматов

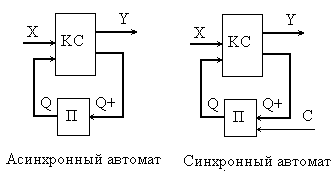
Х – входные сигналы, У – выходные, КС – комбинационная схема, П – память, Q - состояние памяти (внутреннее состояние автомата) в момент времени t, Q+ - сигналы возбуждения памяти или состояние памяти в момент времени , С – тактовый сигнал.