3.10.2 Формула Гаусса-Лежандра

Известно, что на отрезке x[–1;1] свойством ортогональности с единичным весом обладают полиномы Лежандра (2.16)

:

P₀(x)=1;

P₁(x)=x;

P₂(x)=(3x²–1)/2;

P₃(x)=(5x³–3x)/2;



(n+1)P_n+1(x)=(2n+1)xP_n(x)–nP_n–1(x).

Поэтому справедлива квадратурная формула

, (3.20)

где x_i – корни полинома Лежандра. К сожалению, нет общей формулы для корней, но имеются достаточно подробные таблицы корней (например, в [4]).

Коэффициенты квадратурной формулы можно определить из соотношения:

,

а погрешность

.

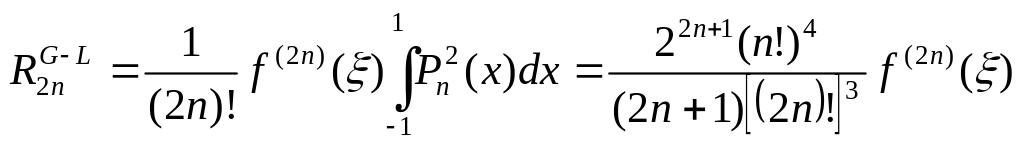Например, для n=3 формула Гаусса-Лежандра имеет вид:

Отметим, что, используя соответствующую замену переменных, формулу Гаусса-Лежандра, так же как и формулу Гаусса-Чебышева, можно применять и для произвольного отрезка интегрирования (см. пример 10).

3.10.3 Формула Гаусса-Лагерра

До сих пор пределы интегрирования были конечные. Но обратите внимание: в квадратурных формулах Гаусса концы отрезка интегрирования не являются узлами квадратурной формулы (в отличие от формул Ньютона-Котеса). Формулы такого типа называются открытыми. Это вселяет надежду, что должны существовать квадратурные формулы для интегралов с бесконечными пределами интегрирования. И они имеются.

На луче x[0,) свойством ортогональности с весом (x)=x^s e^–x обладают полиномы Лагерра

,

где s – любое вещественное число, n – целое положительное число. Следовательно,

(3.21)

где x_i – корни полинома Лагерра n-ой степени. Для них тоже нет общей формулы, поэтому они либо определяются из решения соответствующего алгебраического уравнения, либо из таблиц.

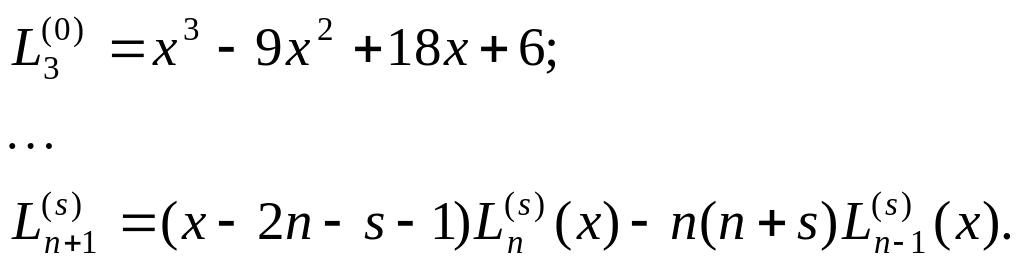
Коэффициенты квадратурной формулы имеют вид:

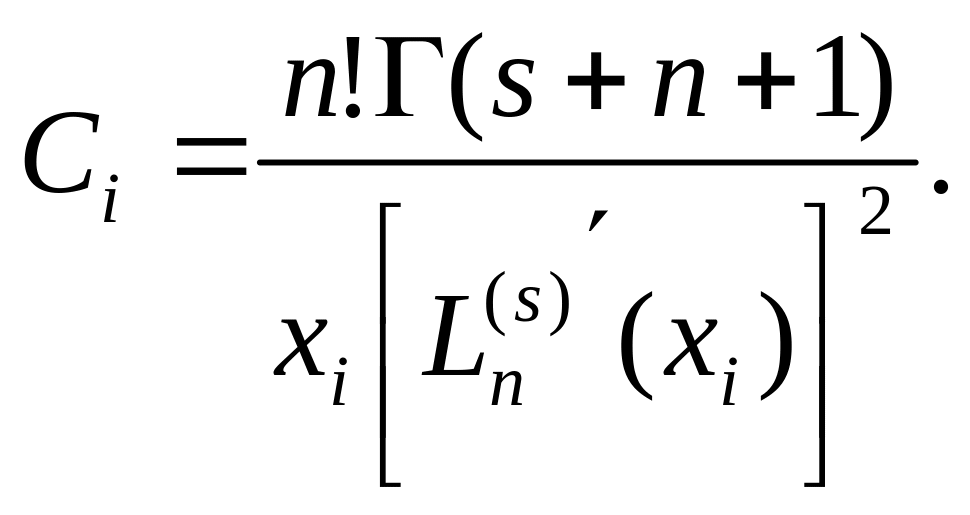
Погрешность квадратурной формулы Гаусса-Лагерра:

.

Здесь Г(x) – гамма–функция. Для целого положительного аргумента k Г(k)=(k–1)!

Например, для s=0 и n=2 формула Гаусса–Лагерра имеет вид

.

3.10.4 Формула Гаусса-Эрмита

На промежутке (– ; +  ) свойством ортогональности с весом обладают полиномы Эрмита

.

H₀(x)=1;

H₁(x)=2x;

H₂(x)=4x²–2;

H₃(x)=8x³–12x;



H_n+1(x)=2xH_n(x)–2nH_n–1(x).

Следовательно,

, (3.22)

где x_i – корни полинома Эрмита n-ой степени. Для них также нет общей формулы, поэтому они либо определяются из решения соответствующего алгебраического уравнения, либо из таблиц.

Коэффициенты квадратурной формулы Гаусса–Эрмита имеют вид:

Погрешность квадратурной формулы Гаусса-Эрмита

.

Например, при n=2 формула Гаусса-Эрмита имеет вид

.

3.11 ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ

НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ

Напомним, что несобственными интегралами называются интегралы с неограниченными пределами интегрирования или с неограниченными подынтегральными функциями. Будем рассматривать сходящиеся несобственные интегралы. Универсальных методов их выражения нет, но можно указать несколько полезных приемов.

3.11.1 Вычисление интегралов с бесконечными пределами интегрирования

Способ 1. Если подынтегральная функция f(x) представима в виде произведения f(x)=(x)g(x), где (x) – одна из весовых функций квадратурных формул Гаусса-Лагерра или Гаусса-Эрмита, а g(x) – функция, не имеющая особенностей, то можно использовать соответствующую квадратурную формулу:

или .

Способ 2. Исходный несобственный интеграл разбиваем на сумму двух интегралов

.

Так как исходный интеграл – сходящийся, то всегда можно выбрать число b таким, чтобы для второго интеграла выполнялось неравенство

, (3.23)

где  – заданная точность вычисления несобственного интеграла.

Тогда, если вычислить первый интеграл (который является собственным), по одной из квадратурных формул, рассмотренных выше, с точностью /2 , то поставленная задача будет решена.

Таким образом, основная трудность здесь – оценка (3.23). В зависимости от вида подынтегральной функции она проводится или аналитически, или численными методами.

Способ 3. Заменой переменной x=1/t интеграл с бесконечным пределом интегрирования можно свести к интегралу от разрывной функции:

,

приемы интегрирования которого рассмотрены ниже.