3.5.3 Формула Симпсона

Аппроксимируем подынтегральную функцию полиномом второй степени, построенным по трем узлам: x_i–1, x_i–1/2, x_i . Интерполяционный полином Лагранжа второй степени имеет вид

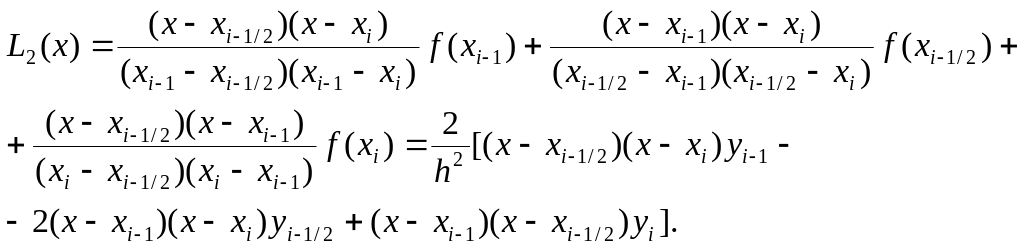
Тогда

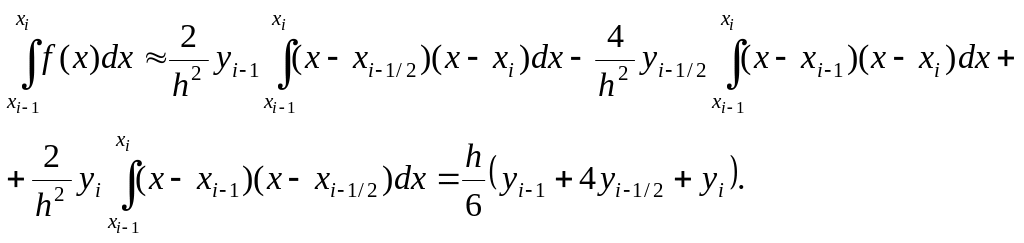
Получили формулу Симпсона для элементарного отрезка [x_i–1,x_i].

Суммируя, получаем составную формулу Симпсона:

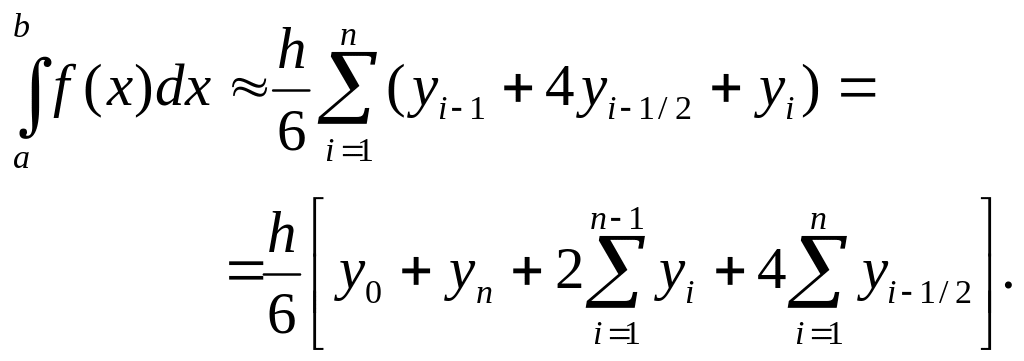(3.9)

Оценим погрешность формулы Симпсона.

Так как эта формула – симметричная, то сразу можно сделать вывод о том, что способ определения погрешности квадратурной формулы по погрешности интерполяционной формулы

будет безрезультатным (проверьте!). Поэтому используем разложение в ряд Тейлора узловых значений функции в окрестности точки x=x_i–1/2:

.

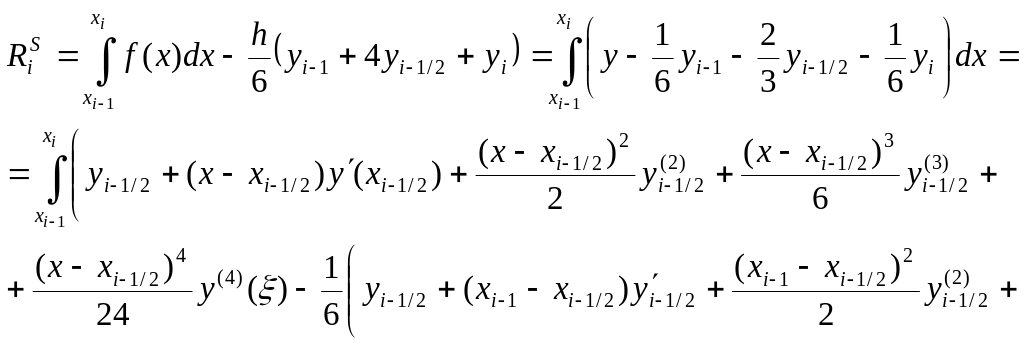
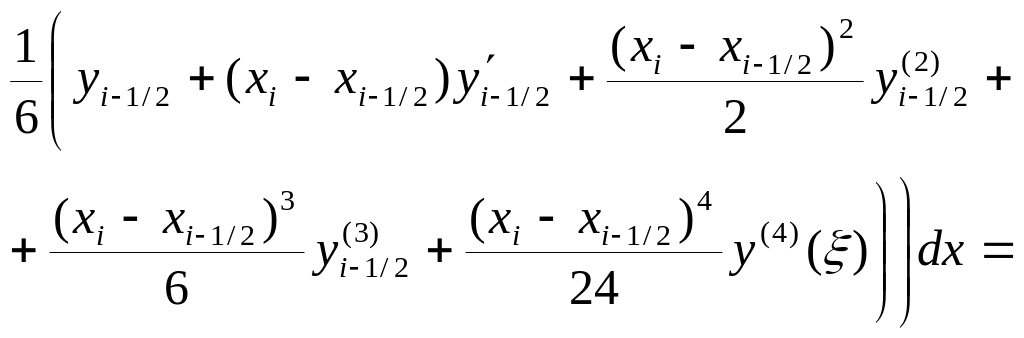
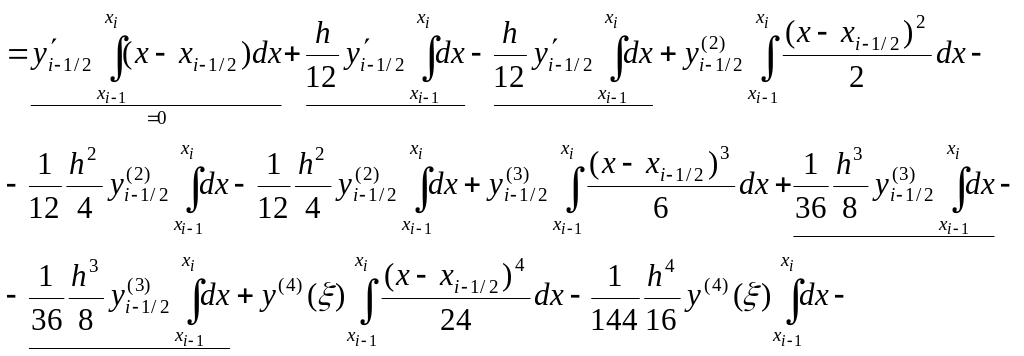
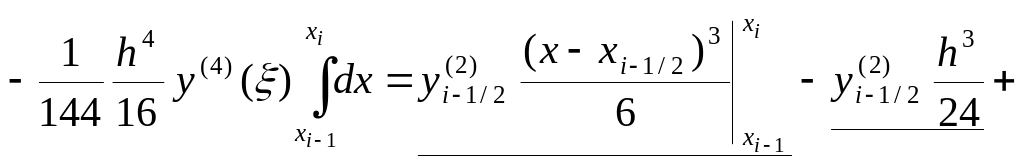
Для составной формулы Симпсона

Таким образом, формула Симпсона существенно точнее, чем формула прямоугольников или трапеций. Порядок точности – четвертый.

Примечание 5. О формуле Симпсона без полуцелых точек.

Формулу Симпсона можно записать по-другому, если пронумеровать насквозь и целые, и полуцелые точки.

Тогда n=2m (то есть n – четное число), новый шаг интегрирования h₁ = h/2=(b–a)/(2m), а формула имеет вид:

(3.10)

Погрешность

.

Конец примечания 5.

3.6 Оценка погрешности методом рунге. Автоматический выбор шага интегрирования

Пусть необходимо вычислить интеграл с заданной предельной погрешностью , то есть необходимо выполнение условия R  . Каким выбрать шаг интегрирования?

Априорную оценку можно получить, потребовав, например, для формулы Симпсона

, или .

На практике такой оценкой пользоваться сложно из-за трудностей оценки четвертой производной.

Поэтому обычно используют апостериорные оценки, например, метод Рунге.

Пусть

,

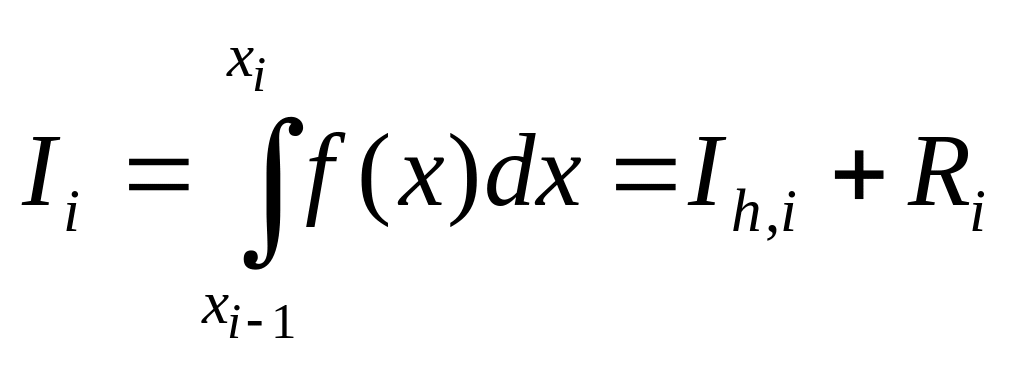где I_h,i – некоторая квадратурная формула, R_i = C_ih^p + o(h^p+1) – погрешность квадратурной формулы, p – порядок точности.

Уменьшим шаг вдвое. Тогда

.

Сравнивая эти два соотношения, получаем формулу Рунге для уточнения найденного значения интеграла:

Первое из подчеркнутых слагаемых – главный член погрешности уточненной формулы.

Тогда последовательность действий по выбору шага интегрирования представляется следующей.

Пусть задана точность вычисления . Проводим по какой-нибудь квадратурной формуле, например, Симпсона (p=4) вычисление интеграла дважды – один раз с шагом h, другой раз с шагом h/2 . По методу Рунге определяем погрешность.

Если оценка

не выполняется, шаг уменьшается еще в два раза, и снова оценивается погрешность

,

и так далее до тех пор, пока не будет выполнено это неравенство. Таким образом, алгоритм сам определяет шаг интегрирования, сообразуясь с заданной точностью. Появляется замечательная возможность – вести интегрирование с крупным шагом на участках плавного изменения функции и с малым шагом на участках более быстрого изменения. Такие алгоритмы называются адаптивными квадратурными алгоритмами.

Отметим, что при реализации таких алгоритмов нет необходимости каждый раз вычислять заново значения функций в узловых точках; достаточно вычислять f(x_i) только во вновь появляющихся узлах. И еще одна рекомендация: необходимо предусмотреть ограничение сверху на число измельчений N, иначе можно доуменьшать до машинного нуля.