3.4 О некорректности операции численного дифференцирования

Итак, при уменьшении шага h погрешность аппроксимации (то есть погрешность метода) уменьшается. Но погрешность решения включает в себя не только погрешность метода, но и погрешность исходных данных, и вычислительную погрешность (см. п.1.1).

Численное дифференцирование относится к таким задачам, в которых погрешность, возникающая при вычислении разностных отношений, может неограниченно возрастать при стремлении шага сетки h к нулю. Поэтому операцию вычисления разностных отношений называют некорректной.

Рассмотрим причину некорректности на примере вычисления разностного отношения

y_i  (y_i–y_i–1)/h ,

представляющего собой формулу левых разностей. Погрешность аппроксимации первой производной составляет

R = M₂h/2,

то есть прямо пропорциональна шагу в первой степени.

С другой стороны, значения функций y_i и y_i–1 вычисляются, вообще говоря, с некоторой погрешностью, то есть

.

Поэтому реально мы найдем

.

Пусть _i  ; _i–1  , где  – верхняя грань погрешностей. Тогда получается, что абсолютную погрешность производной y_i можно оценить по формуле

 = 2 /h.

Итак, если перейти к обозначениям п.1.1, то R  ₂ , а   ₃. Следовательно, при h 0 погрешность метода ₂ 0 , а вычислительная погрешность ₃   (см. рис.3.1).

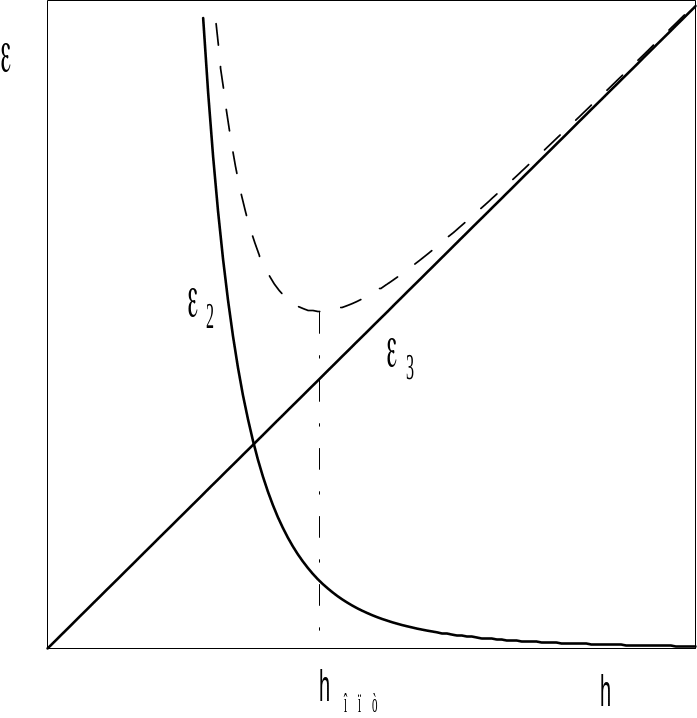
Рис.3.1 – Ошибка численного дифференцирования

Суммарная же погрешность _ = M₂h/2 + 2 /h (пунктирная линия) может убывать при уменьшении шага лишь до некоторого предельного значения h_опт.

Таким образом, если нет возможности менять величину , то вычисления производной надо проводить не с произвольным шагом h, а с шагом, удовлетворяющим условию

h  h_опт , где h_опт =2 .

Отметим, что при вычислении производных более высокого порядка, когда в знаменатель входит h^k (k>1), влияние погрешности в определении y_i сказывается еще больше.

3.5 Численное интегрирование: понятие квадратурных формул

Рассмотрим определенный интеграл

.

Если нет возможности выразить интеграл в известных элементарных или специальных функциях, то применяется приближенное численное интегрирование. Кроме того, если подынтегральная функция задана таблично, то значение интеграла также находится численно.

Рассмотрим методы численного интегрирования, основанные на аппроксимации подынтегральной функции интерполяционными полиномами.

Заменяя подынтегральную функцию, например, интерполяционным полиномом Лагранжа, получаем приближенную формулу:

.

При этом предполагается, что отрезок [a,b] разбит на n частей точками a = x₀ , x₁ , ... , x_n = b, по которым строят интерполяционный полином.

Подставляя выражение для интерполяционного полинома Лагранжа, получаем

,

где .

Таким образом, определенный интеграл можно представить в виде:

, (3.6)

причем коэффициенты С_к не зависят от подынтегральной функции f(x), а только от значений узлов интерполяции.

Это приближенное равенство называется квадратурной формулой.¹ Точки х_к называются узлами квадратурной формулы, а числа С_к – коэффициентами квадратурной формулы.

Разность

называется погрешностью квадратурной формулы.

Отметим, что: 1) погрешность зависит как от расположения узлов, так и от выбора коэффициентов; 2) если функция f(x) – полином степени n, то тогда квадратурная формула будет точной (то есть R_n(f)0), так как в этом случае L_n(x)f(x); 3) погрешность квадратурной формулы можно также представить в другом виде – как интеграл от погрешности интерполяционной формулы Лагранжа:

.

Получим некоторые простые (и в то же время весьма распространенные) формулы численного дифференцирования, используя интерполяционный полином Лагранжа.

Предварительно отметим, что для получения формул численного дифференцирования на некотором отрезке [a, b] достаточно построить квадратурную формулу для интеграла на элементарном отрезке [x_i–1, x_i ], а затем ее просуммировать, т.к.

.
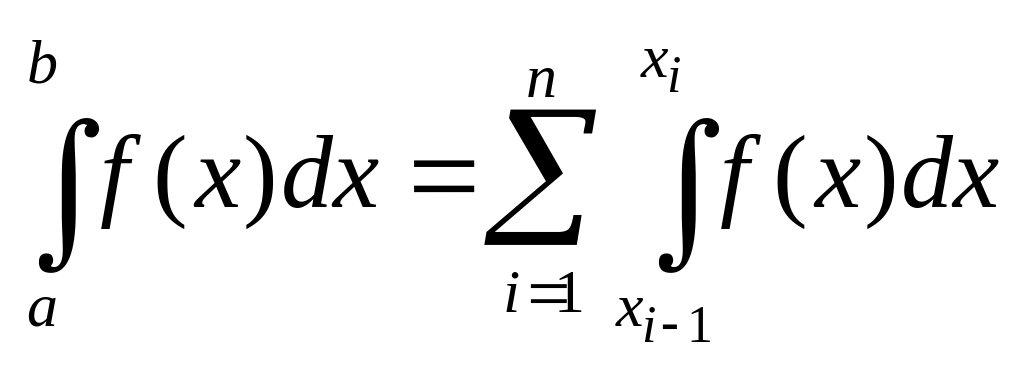