3 ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И

ИНТЕГРИРОВАНИЕ

3.1 ПОЛУЧЕНИЕ ФОРМУЛ ЧИСЛЕННОГО

ДИФФЕРЕНЦИРОВАНИЯ ПУТЕМ АППРОКСИМАЦИИ

Численным дифференцированием пользуются для отыскания производной функции, заданной таблично, а также для приближенного вычисления производной аналитически заданной функции, непосредственное дифференцирование которой затруднительно.

Основная идея получения формул численного дифференцирования состоит в том, что данная функция (табличная или аналитическая) заменяется некоторой аппроксимирующей функцией

которая затем дифференцируется нужное число раз:

3.1.1 Получение формул численного дифференцирования с помощью рядов Тейлора

Пусть функция y=f(x) задана таблично, то есть

y_k = f(x_k), …, k=0, 1, ..., n.

Запишем ряд Тейлора

при х=х₁, х= – h, ограничившись первыми двумя членами:

или, в других обозначениях,

.

Отсюда получаем формулу левых разностей

, (3.1)

где = h^p(х)+o(h^p+1) – погрешность аппроксимации: первый член называется главным членом погрешности, p – порядок аппроксимации производной. В данном случае h=1, таким образом, формула имеет первый порядок аппроксимации.

Если положить х=х₁, а х=h, то получается другая формула численного дифференцирования – формула правых разностей, тоже имеющая первый порядок аппроксимации:

. (3.2)

Если ограничиться четырьмя членами разложения, то для х=h и х= – h соответственно, можно записать

При вычитании получается формула центральных разностей второго порядка аппроксимации:

(3.3)

При сложении получается формула численного дифференцирования для второй производной со вторым порядком аппроксимации:

. (3.4)

Аналогично можно получить аппроксимации производных более высокого порядка и оценку их погрешности. Но этот способ неудобен для практического использования, так как плохо алгоритмизируется и трудоемок.

3.1.2 Получение формул численного дифференцирования с помощью интерполяционного полинома Лагранжа

Построим для заданной функции интерполяционный полином Лагранжа

.

Тогда

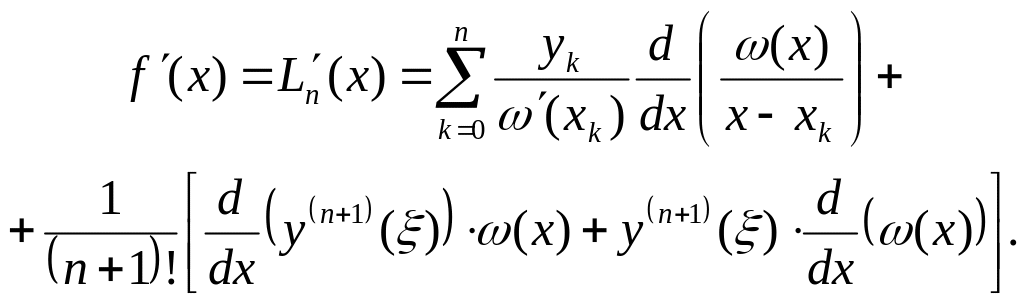
Получили формулу численного дифференцирования для первой производной по (n+1)-ой точке. Погрешность этой формулы состоит из двух слагаемых. Очевидно, что при оценке погрешности в узлах интерполяции х=х_k, первое слагаемое обращается в нуль, и тогда главный член погрешности имеет вид

.

Аналогично получаются формулы численного дифференцирования для производных более высоких степеней.

Пример 1. Получить формулу численного дифференцирования для производной по трем равноотстоящим узлам (n=2).

Интерполяционный полином Лагранжа при n=2 для равноотстоящих узлов будет иметь вид (см. пример из п.2.7):

Тогда

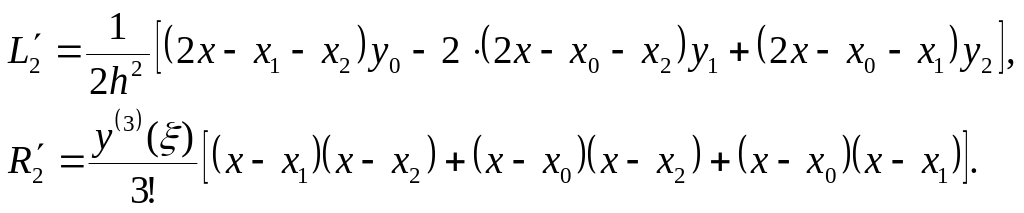
Эти формулы дают выражение для аппроксимации первой производной со вторым порядком. Они справедливы для любого х[x₀; x₂], но чаще используются для узловых точек:

– при х=х₀ получаем требуемую формулу:

;

– полагая х=х₁ и х=х₂ , можно получить другие формулы численного дифференцирования для первой производной по трем точкам:

Записывая интерполяционный полином Лагранжа для четырех узлов (n=3), получаем формулы для аппроксимации первой производной с третьим порядком аппроксимации и так далее.

Таким образом, используя значения функции в n+1 узле, получаем производные с n-ым порядком аппроксимации.

Примечание 1. О центральных разностях.

Если для аппроксимации производной используются центральные разности, то, как это видно из примера, того же самого порядка аппроксимации можно добиться, используя число точек на единицу меньшее, чем при использовании нецентральных разностей.

Конец примечания 1.

3.1.3 Получение формул численного дифференцирования с помощью интерполяционного полинома Ньютона

Построим для заданной функции интерполяционный полином Ньютона:

Тогда аппроксимация первой производной имеет вид:

,

аппроксимация второй производной:

и так далее.

Это так называемые конечно-разностные формулы численного дифференцирования. Безразностные формулы можно получить, выразив разности через значения функции (2.7).

Ясно, что для аппроксимации производных больших порядков необходимо привлекать все больше и больше узловых точек.

Оценка погрешности получается аналогично – как соответствующая производная от погрешности интерполяционного полинома Ньютона.

Например,

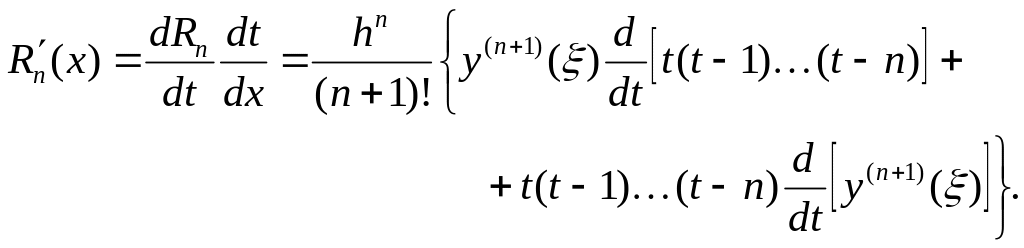
Так как формулы численного дифференцирования обычно используют в узловых точках, то второе слагаемое в этой формуле обращается в нуль, и она принимает вид:

Пример 2. Получить аппроксимацию первой производной в точке х₀ по трем узловым точкам.

При х=x₀ t=0. Тогда для n=2

.

Или, в безразностном виде,

Примечание 2. Об узлах.

Все вышеприведенные формулы были записаны для случая равномерного расположения узлов. Их применение для произвольного неравномерного расположения узловых точек часто приводит понижению точности и даже к грубым ошибкам.

Конец примечания 2.