Задания для самостоятельного выполнения:

Вычислите интегралы: 1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ;

8) ; 9) ; 10) ;

11) ; 12) ; 13) ;

14) ; 15) 16)

Критерии оценки:

оценка	Верно выполненные задания
«3»	Любые 9 заданий
«4»	Любые 9-12 задания с одной не грубой ошибкой
«5»	15-16 заданий, с 1 – 2-мя недочетами

Самостоятельная работа № 15 Решение задач по теме «Приложение интеграла к решению прикладных задач»

Цели изучения темы

• формирование основных понятий по теме «Приложение интеграла к решению прикладных задач»;

• развитие логического и пространственного мышления;

• формирование математической компетенции.

Обучающийся должен:

знать:

• применение интеграла к решению прикладных задач;

уметь:

• вычислять площади плоских фигур;

• решать прикладные задачи, используя определенный интеграл.

Используемая литература:

1. Башмаков М.И. Математика: учебник для нач. и сред. проф. Образования / М.И. башмаков. М.: - Образовательно-издательский центр «Академия»; ОАО «Московские учебники», 2010. – 256 с.

2. Богомолов Н.В. Математика: учеб. для ссузов. М.: Дрофа, 2008.

3. Алгебра и начала анализа: Учебник 10-11 класса общеобразовательных учреждений / А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудницын и др., Под ред. А.Н. Колмогорова. – 14-е изд. – М.: Посвящение, 2010.

Контроль: предоставить самоотчет.

Задания для самостоятельного выполнения:

Задание 1. Найдите площадь фигуры, ограниченной следующими линиями, предварительно сделав рисунок:

1) , y=8, x=1; 2) y = 2cosx, y=1,x= .

Задание 2. Найдите работу против силы выталкивания при погружении шара в воду.

Задание 3. Найдите центр масс однородного прямого кругового конуса.

Задание 4. Вычислите силу давления воды на вертикальную площадку, имеющую форму прямоугольника с основанием 4 м и высотой 2 м. Верхнее основание находится на поверхности воды.

Критерии оценки:

оценка	Верно выполненные задания
«3»	Любые 2 задания
«4»	Любые 3 задания с одной не грубой ошибкой
«5»	Все задания, с 1 – 2-мя недочетами

Самостоятельная работа № 16 «Решение дифференциальных уравнений с разделяющимися переменными. Общие и частные решения».

Цели изучения темы

• формирование основных понятий по теме «Дифференциальные уравнения с разделяющимися переменными. Общие и частные решения»;

• развитие логического и пространственного мышления;

• формирование математической компетенции.

Обучающийся должен:

знать:

• типы задач, приводящие к дифференциальным уравнениям;

• определение дифференциального уравнения;

• определение общего и частного решений дифференциальных уравнений, их геометрической интерпретации;

• методы решения обыкновенных дифференциальных уравнений с разделяющимися переменными.

уметь:

• составлять дифференциальные уравнения на простейших задачах;

• решать дифференциальные уравнения с разделяющимися переменными.

Используемая литература:

1. Богомолов Н.В. Математика: Учебник для ССУЗов. М.: Дрофа, 2009.

2. Соловейчик И.Л. Сборник задач по математике с решениями для техникумов. М.: ООО «Издательский дом «Оникс 21 век», 2003.

3. Шапкин А.С. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями. М.: «Дашков и К»,2007.

Контроль: предоставить самоотчет

Задания для самостоятельного выполнения:

1. Найти все решения дифференциального уравнения

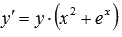
2. Найдите общее решение дифференциального уравнения 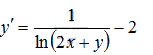и частное решение, удовлетворяющее начальному условию y(0) = e.

3. Решить дифференциальное уравнение

4. Составить уравнение кривой, проходящей через точку M(2;1) и имеющей угловой коэффициент

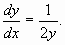
5. Составить уравнение кривой, проходящей через точку M(1;2) и имеющей угловой коэффициент

6. Найти частные решения дифференциальных уравнений:

а)

б)

в)

г)

Критерии оценки:

оценка	Верно выполненные задания
«3»	Любые 4 задания с одной не грубой ошибкой
«4»	Любые 5 заданий с одной не грубой ошибкой
«5»	Все 6 заданий, с 1 – 2-мя недочетами

Самостоятельная работа № 17 «Вычисление определенных интегралов с помощью формул приближенного интегрирования»

Цели изучения темы

• формирование основных понятий по теме «Вычисление определенных интегралов с помощью формул приближенного интегрирования»;

• развитие логического и пространственного мышления;

• формирование математической компетенции.

Обучающийся должен:

знать:

• способы представления функции в виде прямоугольников и трапеций;

• формулу Симпсона;

• выражения для определения предельных абсолютных погрешностей;

уметь:

• вычислять интегралы по формулам прямоугольников, трапеций и формуле Симпсона.

Используемая литература:

1. Богомолов Н.В. Математика: Учебник для ССУЗов. М.: Дрофа, 2009.

2. Соловейчик И.Л. Сборник задач по математике с решениями для техникумов. М.: ООО «Издательский дом «Оникс 21 век», 2003.

3. Шапкин А.С. Задачи по высшей математике, теории вероятностей, математической статистике, математическому программированию с решениями. М.: «Дашков и К»,2007.

Контроль: предоставить самоотчет.

Вопросы для самоконтроля:

1. Вычислить определенный интеграл

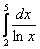
2. Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.

а) Разбив отрезок интегрирования на 3 части.

б) Разбив отрезок интегрирования на 5 частей.

3. Вычислить приближенно определенный интеграл по формуле трапеций с точностью до 0,001.

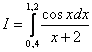
4. Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков

5. Вычислить приближенное значение определенного интеграла  с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Точность вычислений 0,001.

Критерии оценки:

оценка	Верно выполненные задания
«3»	Любые 3 задания
«4»	Любые 4 задания с одной не грубой ошибкой
«5»	Все 5 заданий, с 1 – 2-мя недочетами

Самостоятельная работа 18 Подготовка презентации «История становления теории исследования операций как науки».

Цель:

• формирование познавательного интереса обучающихся к науке «Математика»;

• развитие творческого потенциала;

• формирование навыков исследовательской деятельности;

• развитие навыков самостоятельной работы с источниками информации, информационными технологиями;

• развитие мыслительной деятельности при проектировании, планировании, работе с источниками информации, анализе, синтезе, структурировании информации; самоанализа и рефлексии.

Обучающийся должен:

знать:

• историю становления теории исследования операций как науки.

Описать историю становления теории исследования операций как науки. Привести примеры, где можно применять теорию исследования при решении профессиональных задач.

Контроль: презентация.

Самостоятельная работа № 19 Подготовить сообщение «Применение численного дифференцирования при решении профессиональных задач»

Цель:

• формирование познавательного интереса обучающихся к науке «Математика»;

• развитие творческого потенциала;

• формирование навыков исследовательской деятельности;

• развитие навыков самостоятельной работы с источниками информации, информационными технологиями;

• развитие мыслительной деятельности при проектировании, планировании, работе с источниками информации, анализе, синтезе, структурировании информации; самоанализа и рефлексии.

Обучающийся должен:

знать:

• области применения численного дифференцирования при решении профессиональных задач.

уметь:

• решать профессиональные задачи применяя численное дифференцирование.

Описать основные области применения численного дифференцирования при решении профессиональных задач. Привести примеры.

Контроль: сообщение.