Алгоритм Дейкстры нахождения кратчайшего маршрута от заданной вершины на графе транспортной схемы

1. Заданной вершине x_i начала маршрута присвоить постоянную метку [0; –], где «0» означает, что кратчайшая длина маршрута от вершины x_i до вершины начала равна F_i = 0, так как в данном случае вершина x_i и есть вершина начала маршрута; знак «–» означает, что для исходной вершины исключается из рассмотрения возможность вернуться в эту вершину из любой предшествующей ей смежной вершины, так как, естественно, что входящая в кратчайший маршрут вершина транспортной схемы не может встретиться в нем более одного раза.

2. Определить все вершины x_j, достижимые из смежной им вершины x_i – последней из вершин графа, которым присвоена постоянная метка.

3. Установленным вершинам x_j, не имеющим постоянных меток, присвоить временные метки (F_j = F_i + с_ij; i), где с_ij – вес ребра/дуги между х_i и соответствующей x_j, равный расстоянию между соответствующими пунктами. Если вершина x_j уже имеет временную метку (F_j; k), полученную ранее от другой вершины х_k, и если F_i + с_ij < F_j, то метка (F_j; k) заменяется на (F_j = F_i + с_ij; i).

4. Среди вершин, имеющих временные метки, выбрать вершину, в метке которой (F_s; q) значение расстояния F_s является наименьшим (если таких меток несколько, то выбирается любая их них). Положить q = i, метке данной вершины х_i придать статус постоянной, и процесс определения искомого маршрута продолжить, вернувшись к пункту 2 алгоритма. Если все вершины графа получили постоянные метки, то процесс определения минимальных расстояний вершин графа до вершины начала маршрута завершен.

5. По заданной конечной вершине маршрута и имеющимся меткам вершин определить последовательность вершин соответствующего кратчайшего маршрута и его длину.

П

20

В

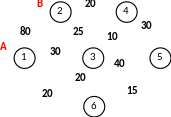
ример. Для приведенного орграфа, вес дуг которого соответствует длинам дорог (км), связывающих смежные вершины, найти по алгоритму Дейкстры кратчайший маршрут между вершинами (1) и (2):

30

2

4

80

25

30

10

А

40

5

3

1

20

20

15

6

1. Вершине х₁ начала маршрута присваиваем постоянную метку [0; –].

2. Для х₁ смежные достижимые вершины без постоянных меток: х₂, х₃. Определяем временные метки этих вершин:

Вершина	Метка	Статус метки
х1	[0; –]	постоянная
х2	(0 + 80; 1) = (80; 1)	временная
х3	(0 + 30; 1) = (30; 1) → [30; 1]	временная → постоянная

Поскольку наименьшее расстояние от начала маршрута среди временных меток имеет вершина х₃, то метке этой вершины придаем статус постоянной.

3. Для вершины х₃, последней с присвоенной постоянной меткой, смежные достижимые вершины: х₄, х₅, х₆. Определяем временные метки этих вершин:

Вершина	Метка	Статус метки
х1	[0; –]	постоянная
х2	(80; 1)	временная
х3	[30; 1]	постоянная
х4	(30 + 10; 3) = (40; 3) → [40; 3]	временная → постоянная
х5	(30 + 40; 3) = (70; 3)	временная
х6	(30 + 20; 3) = (50; 3)	временная

Поскольку наименьшее расстояние от начала маршрута среди временных меток имеет вершина х₄, то метке этой вершины придаем статус постоянной.

4. Для вершины х₄, последней с присвоенной постоянной меткой, смежные достижимые вершины без постоянных меток: х₂, х₅. Определяем временные метки этих вершин:

Вершина	Метка	Статус метки
х1	[0; –]	постоянная
х2	(80; 1), (40 + 20, 4) → (60; 4) → [60; 4]	временная → постоянная
х3	[30; 1]	постоянная
х4	[40; 3]	постоянная
х5	(70; 3), (40 + 30; 4) = (70; 4) → [70; 3, 4]	временная → постоянная
х6	(50; 3) → [50; 3]	временная → постоянная

При заполнении этой таблицы учтено, что:

• вершина х₂ получает две метки (80; 1), (60; 4), оставляем метку (60; 4), в которой указано меньшее значение расстояния от начала маршрута;

• вершина х₅ получает две метки с одинаковым значением расстояния, оставляем обе метки;

• поскольку наименьшее расстояние от начала маршрута среди временных меток имеет вершина х₆, то метке этой вершины придаем статус постоянной; однако поскольку у вершины х₆ нет смежных достижимых вершин с временной меткой, то рассматриваем другие оставшиеся вершины с временной меткой;

• поскольку наименьшее расстояние от начала маршрута среди временных меток имеет вершина х₂, то метке этой вершины придаем статус постоянной; однако поскольку у вершины х₂ нет смежных достижимых вершин с временной меткой, и единственной временной меткой остается вершина х₅, то придавая и ее метке статус постоянной, и поскольку все вершины получили постоянные метки, то заканчиваем процесс определения минимальных расстояний от начала маршрута.

5. Кратчайшие маршруты из х₁ до любой другой вершины определяются от конечного пункта маршрута путем нахождения вершин согласно обратному порядку присвоения вершинам постоянных меток. Обратной последовательностью вершин от х₂ в х₁ является:

х₂ [60; 4] → х₄ [40; 3] → х₃ [30; 1] → х₁.

Следовательно, кратчайший маршрут из х₁ в х₂ определяется последовательностью вершин х₁ → х₃ → х₄ → х₂; общая длина маршрута F*_min = 60 км.

Ответ: кратчайший маршрут из х₁ в х₂: х₁ → х₃ → х₄ → х₂; F*_min = 60 км. #