3. Матричное задание графа
При большом числе вершин и дуг/ребер изображение графа теряет наглядность. В таких случаях, а также для компьютеризации исследований графа используется матричная форма его задания. Основными матричными формами задания графов являются матрица инциденций и матрица смежности вершин.
Строки матрицы инциденций А орграфа соответствуют вершинам, а столбцы – дугам. Элемент матрицы А
аij
=
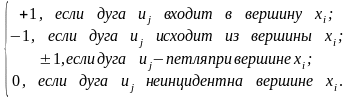
Для неориентированного графа аij = 1, если ребро иj инцидентно вершине хi, т.е. вместо «– 1» и «± 1» в матрице ставится «1».
Пример 1. Составить матрицу инциденций для орграфа:
Рекомендация. Матрицу А предпочтительнее строить по столбцам.
Строки и столбцы матрицы смежности вершин S соответствуют вершинам графа. Элемент матрицы sij равен числу дуг, исходящих из хi-й вершины в хj-ю.
П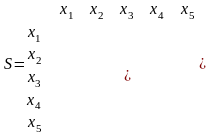
ример
2. Составить матрицу смежности вершин
для орграфа:
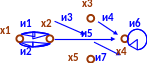
Примечание. Матрица S заполняется по строкам.
Для неориентированного графа матрица S симметрическая, и восстановление графа по матрице можно выполнить по верхней треугольной части этой матрицы.
4. Упорядочение вершин орграфа
Упорядочение вершин связного орграфа без контуров и петель означает построение изоморфного графа с ориентацией всех дуг в одном общем направлении. Упорядочить вершины орграфа можно посредством их группировки, при которой:
вершины первой группы не имеют предшествующих, а вершины последней группы не имеют последующих вершин;
вершины любой другой группы не имеют предшествующих в следующих группах;
вершины одной и той же группы не смежны, т.е. не связаны дугами.
Алгоритм Фалкерсона графического упорядочения вершин орграфа
1. Найти вершины связного орграфа без контуров и петель, в которые не входит ни одна дуга, образовать из них 1-ю группу вершин.
2. Исключить вершины и выходящие из них дуги установленной группы из исходного орграфа.
3. Установить следующую группу вершин, в которые не входит ни одна дуга.
4. Если процесс группировки не окончен, перейти к п.2.
5. Если группировка завершена, то между упорядоченными вершинами воспроизвести дуги исходного орграфа и их вес.
6. Процесс построения орграфа с упорядоченными вершинами, изоморфного исходному, при необходимости, можно продолжить перестановкой вершин внутри групп для уменьшения точек пересечений дуг и перенумерацией вершин последовательно от группы к группе.
П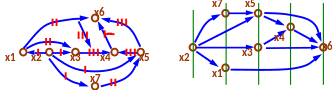
ример.
Построить для данного орграфа изоморфный
с упорядоченными вершинами:
Решение.
1) В вершину х2 не входит ни одна дуга, следовательно, х2 принадлежит 1-й группе вершин, располагаем х2 на 1-й «спице».
2) Исключаем из рассмотрения х6 и исходящие из нее дуги.
3) В оставшемся графе не имеют входящих дуг вершины х1 и х7, следовательно, они образуют 2-ю группу вершин; располагаем их на 2-й «спице» и исключаем их и исходящие из них дуги в исходном графе.
4) Аналогично, 3-я группа образуется вершинами х3 и х5, 4-я – вершиной х4, 5-я – вершиной х7.
5) Соединяем вершины дугами согласно исходному графу.