Тема 12. Графовые модели систем

1. Понятие графа

Граф – это графическое представление связей между состояниями или структурными элементами системы.

Формально конечный граф определяется заданием двух дискретных множеств: множеством вершин Х = {х₁; …; х_n}, где х_i – i-я составная часть системы или i-е состояние системы, и множеством линий связи между вершинами U = {и₁; …; и_m}. Линии связи и_k называются дугами, если задано направление связи, и ребрами, если не указана их направленность, т.е. если связь двунаправленная. Граф с дугами называется ориентированным графом, или орграфом, а с ребрами – неориентированным графом.

П римеры.

Вершины х_i и х_j, связанные дугой/ребром и_k, называются концевыми вершинами этой дуги/ребра. Если концевые вершины совпадают, то дуга/ребро называется петлей. Дуги/ребра с одинаковыми концевыми вершинами называются параллельными. Граф без петель и параллельных линий связи называется простым. Концевые вершины х_i и х_j одной дуги/ребра или дуги/ребра и_k, и_q с общей вершиной называются смежными. Простой граф, в котором каждая пара вершин смежна, называется полным.

Если вершина х_i является концевой для дуги/ребра и_k, то эти х_i и и_k инцидентны: вершина х_i инцидентна дуге/ребру и_k, а дуга/ребро и_k инцидентна вершине х_i.

Т.о., смежность – отношение связности между однородными элементами графа (между вершинами или между дугами/ребрами), а инцидентность – между разнородными (вершинами и дугами/ребрами).

Вершина, не имеющая отношений смежности, называется изолированной.

Графы, находящиеся в отношении эквивалентности, называются изоморфными. Изоморфные графы отличаются только геометрической конфигурацией.

П ример изоморфных графов.

В ряде случаев дугам/ребрам ставятся в соответствие числовые характеристики с_ij (длина пути, интенсивность потока заявок в системах массового обслуживания, время передачи информации от одной x_i к другой x_j смежной вершине, пропускная способность канала связи и т.д.), называемые весом дуг/ребер, а графы с таким весом связей называются взвешенными.

Маршрутом в неориентированном графе называется последовательность попарно смежных ребер (причем одно и то же ребро в маршруте может встречаться несколько раз), соединяющих одну из вершин графа (начало маршрута) с другой вершиной (концом маршрута). Маршрут можно обозначать последовательностью вершин, через которые он проходит. В маршруте одна и та же вершина, в том числе начало и конец маршрута, может встречаться неоднократно. Если начало маршрута совпадает с его концом, то маршрут замкнут, иначе открыт.

Путь в орграфе – это последовательность неповторяющихся дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей. Конечный путь, у которого начальная вершина совпадает с конечной, называется контуром.

В неориентированном графе путь называется цепью, а контур – циклом. Цикл (путь), не содержащий повторяющихся вершин, называется простым. Если существует путь из х_i в х_j, то вершина х_i называется предшествующей вершине х_j, а х_j – последующей за х_i.

О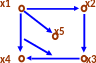 рграф (неориентированный граф) называется связным, если он не имеет изолированных вершин или изолированных комплексов вершин. Орграф называется сильно связным, если для лю-

бых двух вершин х_i и х_j существуют пути из х_i в х_j

и из х_j в х_i, как, например, путь из х₂ в х₅ и из х₅ в х₂

на приведенном сильно связном орграфе:

Граф называется эйлеровым, если содержит эйлеров цикл (путь), т.е. цикл (путь), включающий все ребра (дуги) этого графа. Обход по эйлерову циклу из какой-либо вершины выполняется по всем ребрам графа по одному разу с возвращением в эту исходную вершину. Конечный неориентированный связный граф является эйлеровым тогда и только тогда, когда количество ребер, инцидентных каждой вершине четно (при этом петлю следует рассматривать и как удвоенное ребро).