Средняя квадратичная скорость молекул

Уравнение, определяющее

; ; ; = .

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа

Различные формулы для

= ; Использовали формулу . Учли, что = ; .

Термодинамическая температура является мерой средней кинетической энергии поступательного движения молекул идеального газа, и формула раскрывает молекулярно-кинетическое толкование температуры. При температурах, близких к 0К, это выражение несправедливо, т.е. не пропорционально Т. Поэтому некорректно говорить о том, что при 0К движение молекул прекращается. В настоящее время доказано, что при 0К частицы вещества совершают нулевые колебания. Здесь « » - постоянная Больцмана, равная 1,38∙10^-23 Дж/К.

Основы термодинамики Закон Больцмана о равномерном распределении энергии по степеням свободы

Число степеней свободы молекул – число независимых переменных, полностью определяющих положение системы в пространстве.

Число степеней свободы для различных моделей молекул

Газ	Модель молекулы	Число степеней свободы (i)
		Поступатель-ные (iпост)	Вращатель-ные (iвращ)	Колебательные (iколеб)	Всего
Одноатомный	Материальная точка	3	-	-	3
Двухатомный	Две материальные точки, жесткая связь (например, стержень)	3	2	-	5
Двухатомный	Две материальные точки, нежесткая связь (пружина)	3	2	2	7
Трехатомный, многоатомный	Три (много) атома, жесткая связь	3	3	-	6

Энергия, приходящаяся на поступательную степень свободы

Независимо от общего числа степеней свободы молекул три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения .

Закон Больцмана о равномерном распределении энергии по степеням свободы

Для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная , а на каждую колебательную степень свободы – в среднем энергия, равная . Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движения), но и потенциальная энергия, причем средние значения кинетической и потенциальной энергий одинаковы.

Средняя кинетическая энергия молекулы

,

где i = i_пост + i_вращ + 2i_колеб (i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы).

Внутренняя энергия термодинамической системы

Внутренняя энергия U – энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц.

• К внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.

• Внутренняя энергия – однозначная функция термодинамического состояния системы.

• При переходе системы из одного состояния в другое изменение внутренней энергии определяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода.

Внутренняя энергия 1 моль идеального газа

В идеальном газе взаимная потенциальная энергия молекул равна нулю (молекулы не взаимодействуют), поэтому U_m равна сумме кинетических энергий N_A молекул.

Внутренняя энергия произвольной массы газа

,

m – масса газа; М – молярная масса; - количество вещества; k - постоянная Больцмана; R – молярная газовая постоянная; N_A - постоянная Авогадро; i – число степеней свободы молекулы; Т – термодинамическая температура.

Первое начало термодинамики

Первое начало термодинамики – закон сохранения и превращения энергии применительно к термодинамическим процессам.

Теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.

В дифференциальной форме:

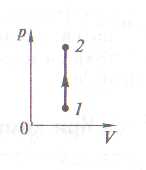
Работа, совершаемая идеальным газом при его расширении

Элементарная работа:

Полная работа при изменении объема от V₁ до V₂

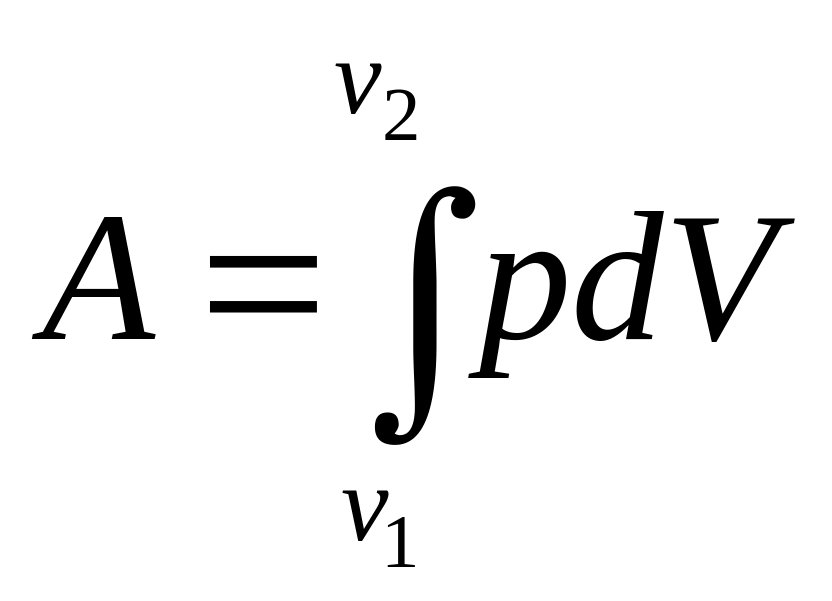
Теплоемкости. Уравнение Майера

• Теплоемкость: - Величина, определяемая количеством теплоты, которое необходимо сообщить телу (системе), чтобы повысить его температуру на 1К (Дж/К)

• Удельная теплоемкость (Дж/кг∙К)

• Молярная теплоемкость (Дж/моль∙К)

• Связь удельной и молярной теплоемкостей (M - молярная масса; m – масса вещества; - количество вещества.

Молярные теплоемкости при постоянных объеме и давлении

• Молярная теплоемкость при постоянном объеме равна изменению внутренней энергии 1 моль газа при повышении его температуры на 1К.

Или , где i – число степеней свободы.

• Молярная теплоемкость при постоянном давлении .

Уравнение Майера

Толкование уравнения Майера: С_р всегда больше С_V на величину молярной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.

Применение первого начала термодинамики к изопроцессам

Изопроцессы - равновесные процессы, в которых один из основных параметров поддерживается постоянным.

Изохорный процесс V=const

Работа - - газ не совершает работы над внешними телами.

Первое начало термодинамики

Теплота, сообщенная газу в изохорном процессе, идет на увеличение его внутренней энергии.

Теплота. Внутренняя энергия.

Изобарный процесс (р=const)

Изобара – в координатах р, V – прямая, параллельная оси V.

Работа изобарного расширения

Из уравнения Клапейрона - Менделеева получаем .

Физический смысл молярной газовой постоянной

Если в выражении работы изобарного расширения , Т₂ – Т₁= 1К, то для 1 моль газа R=A, т.е. молярная газовая постоянная R численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1К.

Теплота

В изобарном процессе при сообщении газу массой m количества теплоты его внутренняя энергия возрастает на величину dU и при этом газ совершает работу . Внутренняя энергия -

Изотермический процесс (Т=const)

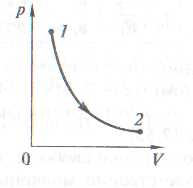
В координатах р, V – гипербола (pV = const). Это изотермическое расширение.

Первое начало термодинамики

Все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.

Внутренняя энергия

При Т=const внутренняя энергия идеального газа не изменяется.

Теплота

Адиабатный и политропный процессы

Адиабатный процесс

Адиабатный процесс – процесс, при котором отсутствует теплообмен между системой и окружающей средой.

Это условие на практике неосуществимо. Оно выполняется только для быстро протекающих процессов.

Первое начало термодинамики

В случае адиабатного процесса система совершает работу за счет убыли внутренней энергии системы.

Уравнение адиабатного процесса (уравнение Пуассона)

Уравнения адиабатного процесса в переменных Т, V и р, Т

Показатель адиабаты (показатель Пуассона)

Для одноатомных газов i =3, ɣ = 1,67; для двухатомных – i = 5; ɣ = 1,4.

i – число степеней свободы; - соответственно молярные и удельные теплоемкости при постоянных давлении и объеме.

Адиабата – в координатах p,V – это гипербола.

Сравнение адиабатного и изотермического процессов

В адиабатном ( ) и изотермическом (pV = const) процессах наблюдаются существенные различия в характере изменения давления при расширении (рис. а) и сжатии (рис. б). Поскольку ɣ>1, адиабата идет круче, чем изотерма. Это можно объяснить тем, что при адиабатном сжатии газ нагревается (увеличение р обусловлено не только уменьшением V (как при изотермическом процессе), но и повышением температуры). При адиабатном расширении газ охлаждается (уменьшение р обусловлено не только увеличением V (как при изотермическом процессе), но и уменьшением температуры).

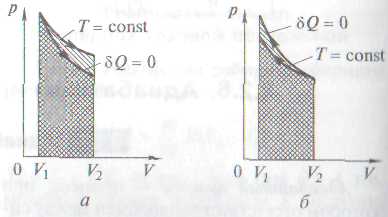
Работа газа в адиабатном процессе

Политропный процесс

Политропный процесс – процесс, в котором теплоемкость остается постоянной.

C = const

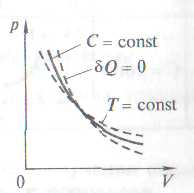
Уравнение и график политропного процесса

Политропа – график (гипербола) зависимости между параметрами

состояния C = const. (n – показатель политропы, )

Частные случаи политропного процесса

С=0	n=γ	pVγ=const	Уравнение адиабаты
C=	n=1	pV=const	Уравнение изотермы
C=Cp	n=0	р=const	Уравнение изобары
C=CV	n=±	V=const	Уравнение изохоры

Сравнение различных газовых процессов

Название процесса	Условие процесса	Закон	Первое начало термодинамики применительно к процессу	Изменение внутренней энергии dU	Работа А
Изотермический	T=сonst	PV=const		0
Изохорный	V=const				0
Изобарный	Р=const
Адиабатный	=0
Политропный	C=const