Физические модели в механике
Материальная точка
Тело, обладающее массой, размерами которого можно пренебречь.
Система материальных точек
Произвольное макроскопическое тело или систему тел можно мысленно разбить на малые взаимодействующие между собой части, каждая из которых рассматривается как материальная точка.
Абсолютно твердое тело
Тело, которое ни при каких условиях не может деформироваться и при всех условиях расстояние между двумя точками этого тела остается постоянным.
Абсолютно упругое тело
Тело, деформация которого подчиняется закону Гука, а после прекращения действия внешних сил принимает свои первоначальные размеры и форму.
Абсолютно неупругое тело
Тело, полностью сохраняющее деформированное состояние после прекращения действия внешних сил.
Механическое движение
Система координат
В простейшем случае это прямоугольная декартова система координат ХУZ.
- радиус-вектор
это вектор перемещения, проведенный из
начального положения движущейся точки
в ее положение в данный момент времени
(рис. 1).
Кинематические уравнения движения материальной точки
или
Траектория
Геометрическое место точек, описываемое движущейся материальной точкой относительно выбранной системы координат. Различают прямолинейное движение, криволинейное движение, движение по окружности и т.д.
Поступательное движение
Движение, при котором любая прямая, жестко связанная с движущимся телом и проведенная через две произвольные точки данного тела, остается параллельной самой себе.
Вращательное движение
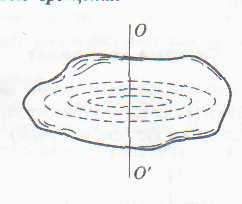
Движение, при котором все точки движутся по окружностям, центры которых лежат на одной прямой ОО, называемой осью вращения (рис.2).
Кинематика поступательного движения
Скорость – векторная величина, которая определяет быстроту движения и его направление в данный момент времени (измерение в м\с).
Средняя скорость
Мгновенная
скорость
Модуль мгновенной
скорости
.
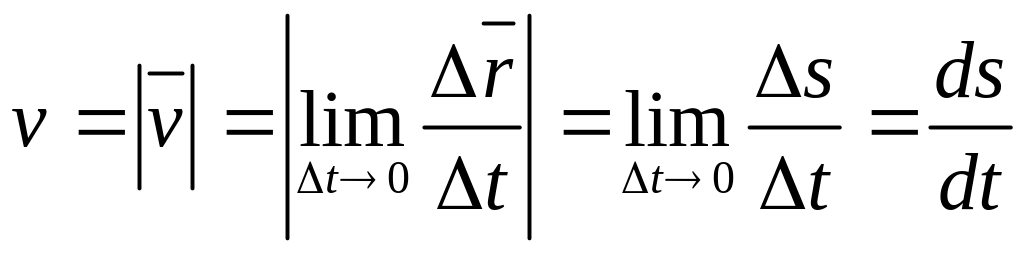
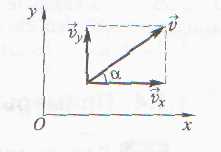
Движение в одной
плоскости
.
Ускорение и его составляющие
Ускорение – характеристика неравномерного движения, определяющая быстроту изменения скорости по модулю и направлению (измерение в м\с2).
Среднее ускорение
;
Мгновенное
ускорение
;
Тангенциальное
ускорение
;
Нормальное ускорение характеризует быстроту изменения скорости по направлению (направлено к центру кривизны траектории).
;
Полное ускорение
при криволинейном движении
.
Это геометрическая сумма тангенциальной и нормальной составляющих ускорения.
Классификация движения в зависимости от тангенциальной и нормальной составляющих ускорения
Тангенциальное ускорение |
Нормальной ускорение |
Движение |
0 |
0 |
Прямолинейное равномерное |
|
0 |
Прямолинейное равнопеременное |
= |
0 |
Прямолинейное с переменным ускорением |
0 |
|
Равномерное по окружности |
0 |
|
Равномерное криволинейное |
|
|
Криволинейное равнопеременное |
= |
|
Криволинейное с переменным ускорением |
=
=
Равномерное
движение (
;
).
Пройденный путь:
при
;
;
при
;
.
Равноускоренное
движение (
).
Скорость: при
;
;
;
При
;
;
;
Пройденный путь:
при
;
;
при
;
.
Вычисление пройденного пути
Путь, пройденный
материальной точкой за промежуток
времени от
до
;
Путь, пройденный
материальной точкой за время
при равномерном движении
;
Путь, пройденный
материальной точкой за время
при равноускоренном движении
.
Свободное падение тел
Исходные данные |
|
||
Кинематические уравнения движения |
|
||
Проекции кинематических уравнений
на ось
|
=
|
||
Путь, пройденный телом в свободном падении в момент времени |
При
|
Свободное падение тела без начальной скорости ( =0). |
Продолжительность свободного падения
Скорость
|
(
– радиус Земли) оно движется с постоянным
ускорением
,
направленным вертикально вниз (
= 9,8 м\с2 – ускорение свободного
падения)
- общее векторное равенство,
описывающее движение
тела с постоянным ускорением
из точки с
начальной скоростью
.
в любой момент времени
+
;
- Ось направлена вертикально
вниз.
;
Начало отсчета помещено
в точку начала движения
Принять
=0
=0
Движение тела, брошенного вертикально вверх
Исходные данные |
|
Кинематические уравнения движения |
- общее векторное равенство, описывающее
|
Проекции кинематических уравнений на ось в любой момент времени |
|
Время подъема |
выражение для .
|
Высота подъема |
|
Общее время движения |
Откуда и получается выражение для |
Время падения |
|
Конечная скорость движения |
|
тела в любой момент движения равно
ускорению свободного падения
(
=
)
движение тела с
постоянным ускорением
из
=
точки
с начальной скоростью
- Ось направлена вертикально вверх.
;
- В
верхней точке
=
0, т.е. 0=
,
откуда и получается
При приземлении
;
(равно времени подъема)
;
.
Конечная скорость движения по модулю
равна начальной скорости. Знак «минус»
показывает, что направления конечной
скорости и оси У не совпадают