3 Кинематика

8.Общие понятия. Два метода исследования движения

• В кинематике рассматриваются общие свойства движения тел без выяснения причин его возникновения. По образному выражению Н.Е. Жуковского "кинематика есть геометрия движения". В отличие от теоретической механики, в которой изучается движение абсолютно твердого тела, в кинематике сплошных сред изучается движение деформируемых тел: в процессе движения изменяется их форма и расстояние между двумя любыми частицами. Деформируемость является главной кинематической особенностью сплошных сред вообще и жидкостей и газов в частности.

• Движение жидкости может быть определено, если в любой момент времени известны векторы скоростей всех ее частиц, другими словами, если известно пространственновременное поле скоростей. Задача кинематики  определение этого поля.

• Существует два метода изучения частиц. Один их них, называемый методом Лагранжа, изучает движение в пространстве каждой индивидуальной частицы; другой, называемый методом Эйлера, изучает движение, происходящее в каждой точке пространства в любой момент времени, а поведением отдельных частиц не интересуется. В первом случае положение каждой частицы будет определяться координатами x₀, y₀, z₀ заданными в некоторый момент времени t=t₀. Следовательно, в любой другой момент времени t, не совпадающий c t₀, координаты частицы определяются функциями

• x=f₁(x₀, y₀, z₀,t),

• y=f₂(x₀, y₀, z₀,t),

• z=f₃ (x₀, y₀, z₀,t).

Аргументы x₀, y₀, z₀, t называются переменными Лагранжа. При использовании метода Эйлера все векторные элементы движения изучаются как функции от координат и времени, т.е. от четырех аргументов x, y, z, t, называемых переменными Эйлера. Например, скорость частиц может быть представлена в виде

• 

В современной гидрогазодинамике чаще применяют метод Эйлера.

9.Поле скоростей и ускорений

Эйлерово поле скоростей выражается в виде

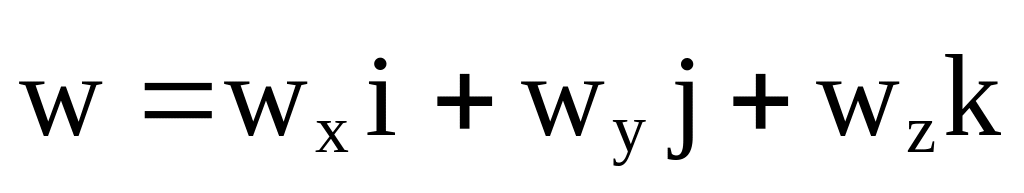• (3.1)

где w_x(x,y,z,t), w_y(x,y,z,t), w_z(x,y,z,t)  проекции компонент вектора скорости,  единичные векторы (орты), направленные по осям x,y,z (рис. 14).

Любое изменение компоненты скорости в окрестности некоторой точки определяется всеми четырьмя аргументами: x, y, z, t. Например, изменение x  компоненты скорости (полный дифференциал) по правилу дифференцирования функции многих переменных равно

• 

и компоненты перемещений не являются независимыми и равны: dx=w_xdt, dy=w_ydt, dz=w_zdt. Подставляя эти выражения в ранее записанное и деля его на dt, получим

• 

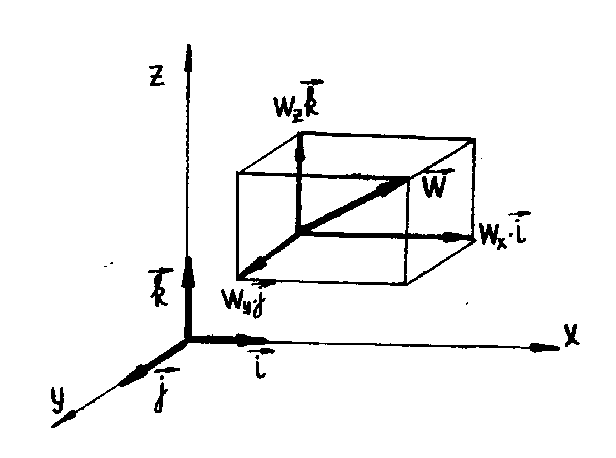
  Рисунок 3.1 - Вектор скорости и его компоненты

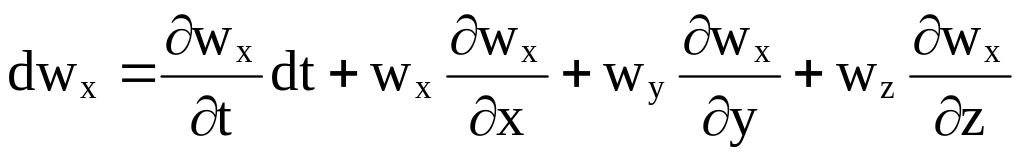  (3.2)

Полученное выражение является полной, или субстанциальной производной, представляющей собой быстроту изменения x  компоненты скорости частицы жидкости. Величина

• 

x  компонента вектора ускорения. Аналогично:

• , .

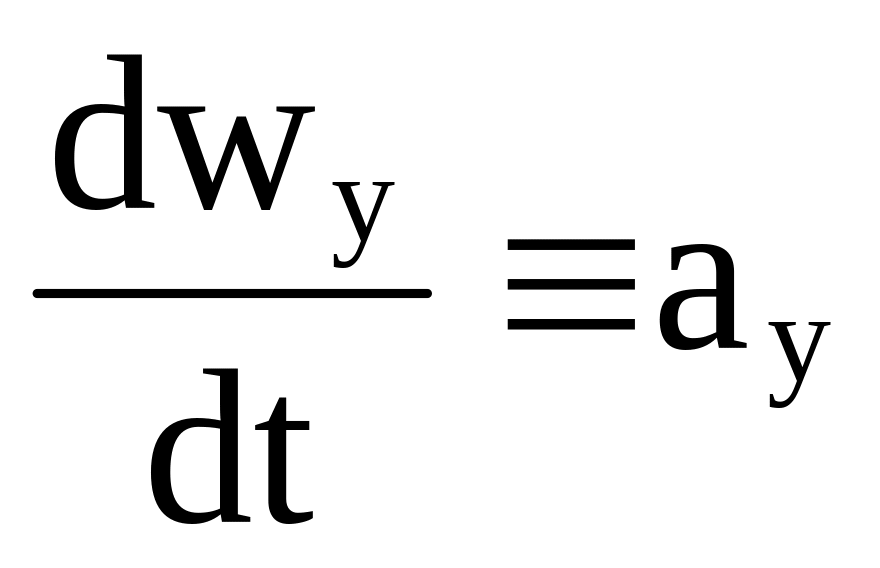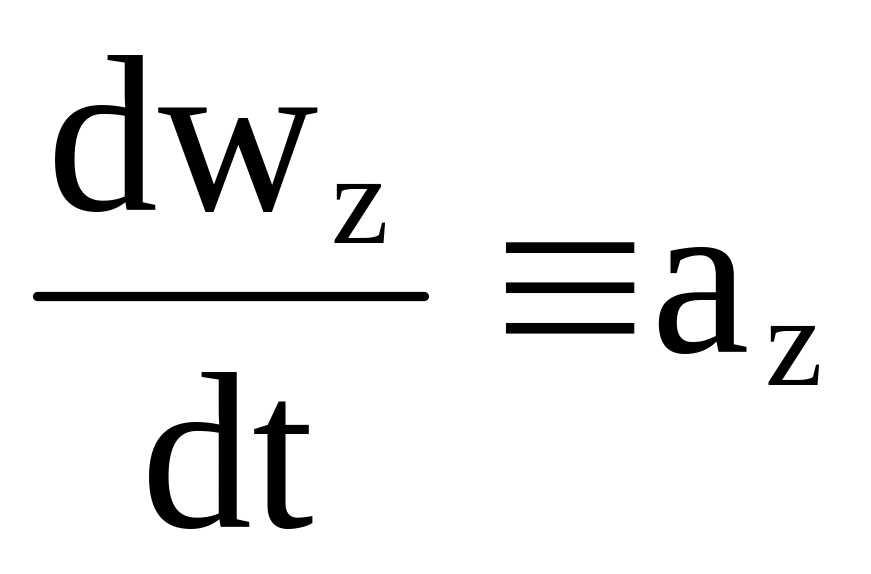Таким образом, компоненты ускорения

• (3.3)

  (3.4)

  (3.5)

  

Вектор ускорения можно записать в виде

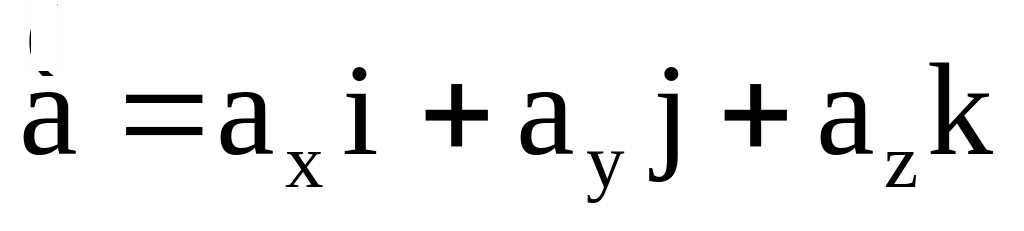• , (3.6)

или, применяя оператор Гамильтона

• ,

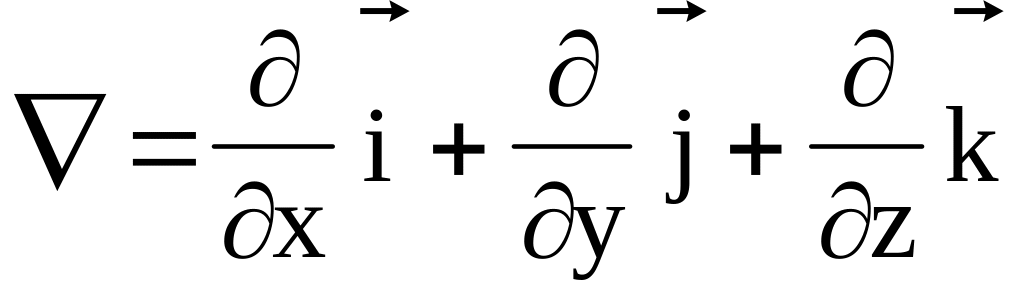ускорение жидкой частицы можно представить в виде

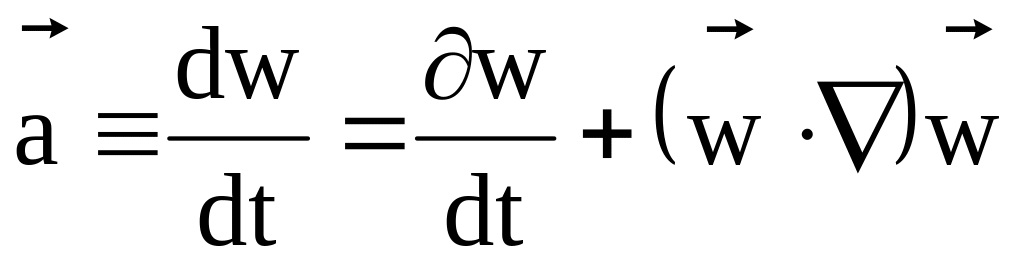• . (3.7)

Первое слагаемое правой части называют локальными составляющими, второе  конвективными. Если все локальные составляющие равны нулю, то движение жидкости является стационарным. Если к тому же и все конвективные составляющие равны нулю, движение является равномерным, что соответствует плоскопараллельному движению.

Изменение любых других характеристик движения или свойств жидкости, являющихся не только векторными, но и скалярными величинами (температура, плотность, концентрация и др.), может рассматриваться подобно изменению скорости. Например, быстрота изменения температуры

• ,

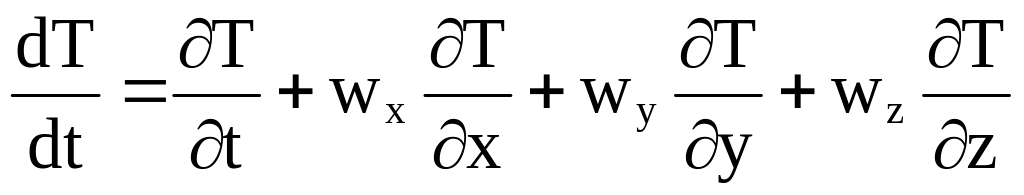или

• .

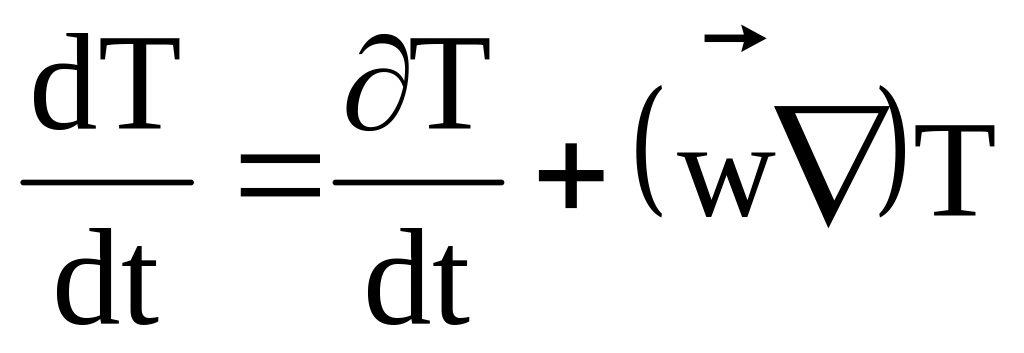В практике часто пользуются понятиями средних скоростей. Среднее за промежуток времени t₀ значение скорости

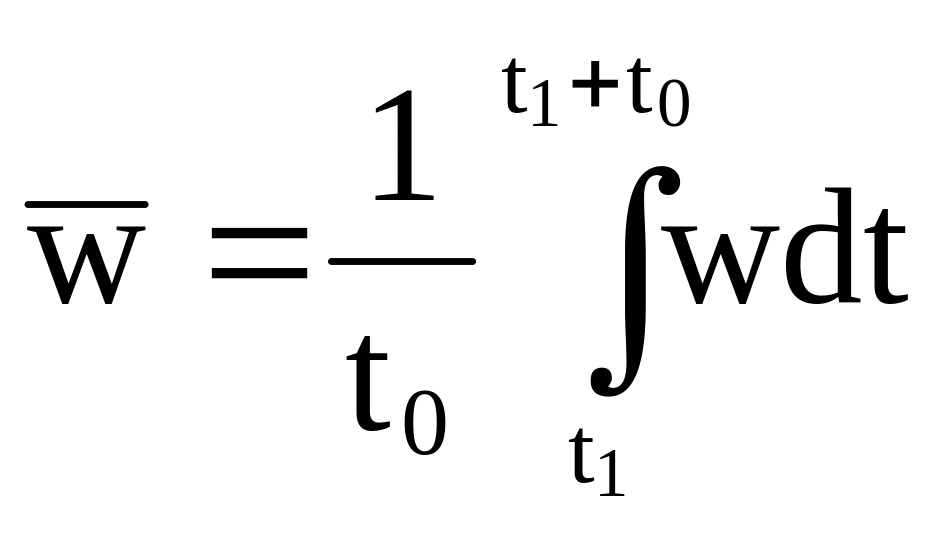• , (3.8)

среднее по некоторой площади s значение скорости

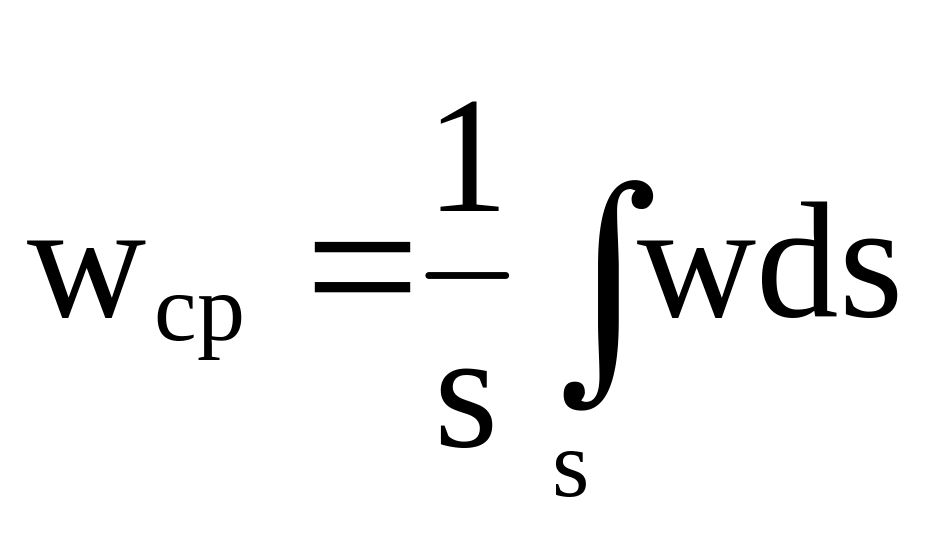• (3.9)