7.Давление жидкости на плоские и криволинейные стенки. Закон Архимеда

Предположим, что плоская стенка площадью s, наклоненная к горизонту под углом , ограждает некоторую массу неподвижной жидкости (рис. 11). Определим силу, с которой жидкость действует на площадку (сила гидростатического давления). В каждой точке площадки гидростатическое давление равно р; сила, действующая на элементарную площадку (ds равна dP = pds, а искомая сила Р может быть найдена как сумма параллельных сил dP:

.

Но в любой точке гидростатическое давление равно р = р₀+gh, поэтому

Рисунок 2.9 К определению сил давления

.

Выберем координатные оси таким образом, что ось Oz будет направлена вниз вдоль стенки, а ось Ох совпадет с линией пересечения плоскости стенки со свободной поверхностью жидкости. В этой координатной системе глубину h можно выразить через координаты точки x и z, например, h=zsin. Теперь силу P можно определить по формуле

или

Подинтегральное выражение в последней формуле можно рассматривать как статический момент площадки ds относительно оси Оx, а интеграл представляет собой сумму статических моментов элементов площадки, т.е. статический момент площади s, который, как известно, равен произведению этой площади на расстояние от ее центра тяжести до оси моментов. Поэтому,

и

P=p₀s+g z_сsin s.

Т.к. z_сsin=h_с, то

P=p₀s+gh_cs,

или за вычетом внешнего давления на свободную поверхность p₀s, передаваемого жидкостью по закону Паскаля,

P=gh_cs. (2.22)

Произведение h_cs представляет собой объем цилиндра с площадью основания s и высотой h_c, поэтому последнюю формулу можно прочитать так: сила давления жидкости на плоскую стенку равна весу жидкости в объеме цилиндра с основанием s и высотой, равной глубине погружения центра тяжести. (Заметим, что точка приложения силы гидростатического давления может не совпадать с центром тяжести, или точкой приложения силы тяжести).

Рассмотрим давление жидкости на криволинейную стенку (abcd с площадью s) (рис. 12). Силу давления можно разложить на составляющие , , :

Рисунок 2.10 Давление жидкости на криволинейную стенку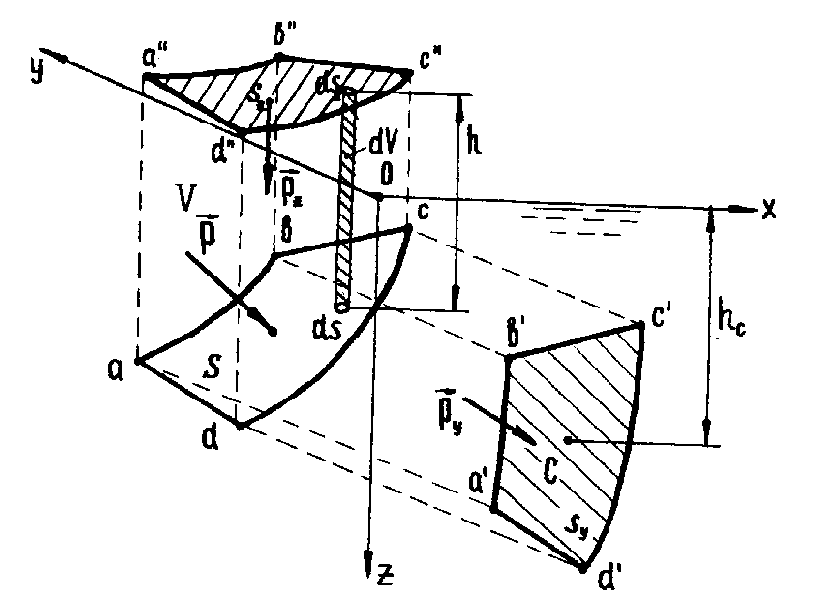

.

Величина этой силы

.

Проекция криволинейной поверхности abcd на координатную плоскость xOz есть плоская фигура abcd, поэтому горизонтальная составляющая силы давления

P_y=gs_yh_c,

где s_y  площадь проекции a'd'c'd',

h_c  глубина погружения центра тяжести стенки. Аналогично

P_x=gs_xh_c

Вертикальная составляющая силы давления

Произведение hds_z можно рассматривать как элементарный объем dV, тогда

, (2.23)

где V'  объем вертикального столба (abcdabcd), называемого телом давления.

Таким образом, вертикальная составляющая силы давления жидкости равна весу жидкости в объеме вертикального столба, опирающегося на заданную криволинейную поверхность и ограниченного плоскостью свободной поверхности.

Закон Архимеда. Определим давление жидкости на погруженное в него тело (рис. 2.11). Горизонтальные составляющие Р_x= т.к. P_x= , аналогично и Р_y=0, поэтому сила давления на всю поверхность погруженного тела

Проведя линию ab, разделим тело на две части  верхнюю и нижнюю.

Рисунок 2.11 К выводу закона Архимеда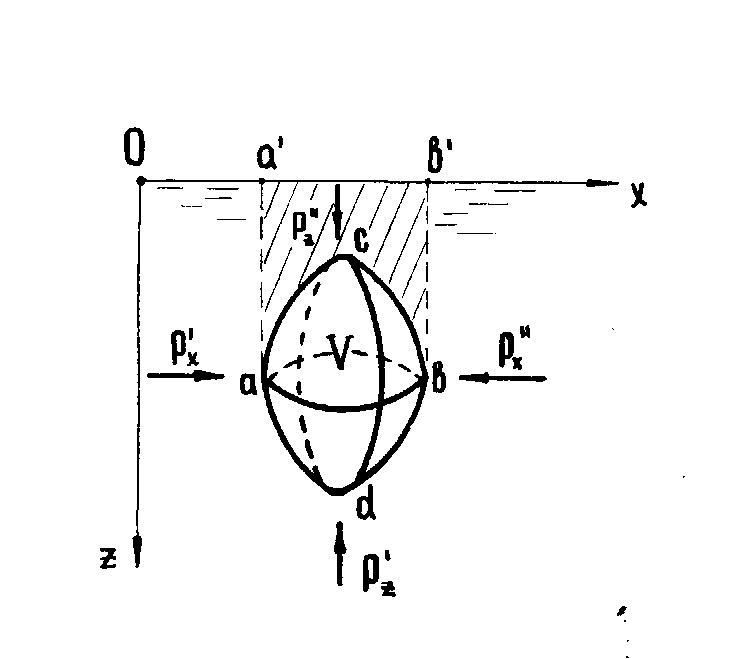

Тогда

,

где

, a .

Разница объемов двух тел давления

 .

равна объему погруженного тела V(abcda) или просто V. Т.к. , то равнодействующая P_z положительна и направлена снизу вверх:

P_z = Vg (2.24)

Таким образом, по закону Архимеда сила, с которой жидкость действует на погруженное в нее тело, равна весу жидкости в объеме погруженного тела. Эта сила называется Архимедовой подъемной силой.