
- •Конспект лекций
- •Конспект лекций
- •6.090500 “Энергетический менеджмент“
- •3 Кинематика 27
- •4 Динамика. Основные уравнения 36
- •5 Гидравлические расчеты промышленных газоходов и трубопроводов 42
- •6 Истечение жидкостей и газов через отверстия, насадки и сопла 60
- •7 Применение уравнения бернулли в технических устройствах и расчетах 65
- •8 Струйное движение 70
- •9 Экспериментальные исследования гидродинамических процессов 85
- •10 Движение многофазных сред 97
- •Введение
- •1 Основные понятия
- •2 Равновесие жидкости (статика)
- •1. Условие равновесия (закон Паскаля)
- •2. Уравнение равновесия Эйлера. Основное дифференциальное уравнение гидростатики
- •3.Равновесие несжимаемой жидкости под действием сил тяжести
- •4.Равновесие несжимаемой жидкости при наличии негравитационных массовых сил
- •4.1.Равноускоренное движение жидкости в горизонтальном направлении
- •4.2.Равновесие жидкости, покоящейся относительно сосуда и вращающейся относительно вертикальной оси
- •5.Уравнения гидростатики для сжимаемых сред
- •6.Статика двух газов. Дымовая труба
- •7.Давление жидкости на плоские и криволинейные стенки. Закон Архимеда
- •3 Кинематика
- •8.Общие понятия. Два метода исследования движения
- •9.Поле скоростей и ускорений
- •10.Линия тока, трубка тока, траектория
- •11. Уравнение неразрывности или сплошности (Уравнение расхода)
- •12.Вихревое и безвихревое движение
- •4 Динамика. Основные уравнения
- •13.Дифференциальное уравнение движения несжимаемой идеальной (невязкой) жидкости (уравнение движения Эйлера)
- •14.Дифференциальное уравнение движения несжимаемой реальной (вязкой ) жидкости (уравнение Навье-Стокса)
- •15.Уравнение Навье-Стокса для сжимаемой жидкости
- •16.Уравнение Бернулли для идеальной несжимаемой жидкости
- •5 Гидравлические расчеты промышленных газоходов и трубопроводов
- •17.Уравнение Бернулли для потока реальной жидкости
- •18.Уравнение Бернулли в избыточных давлениях
- •19. Потери на трение
- •19.1.Потери на трение в потоке несжимаемой жидкости
- •19.2. Потери на трение в потоке сжимаемых жидкостей (газов высокого давления)
- •19.3. Рисунок 5.2 Зависимость потерь давления от начального давления газа Коэффициент трения
- •20.Потери на местные сопротивления
- •21. Рисунок 5.11. Теорема Борда
- •22.Учет взаимного влияния местных сопротивлений
- •23.Гидростатические потери (потери геометрического давления)
- •24.Общие принципы расчета сложных гидравлических систем
- •Истечение жидкостей и газов через отверстия, насадки и сопла
- •6.1 Истечение несжимаемых сред через отверстия
- •6.2 Истечение несжимаемых сред через насадки
- •6.3 Истечение сжимаемых газов (газов высокого давления )
- •7 Применение уравнения бернулли в технических устройствах и расчетах
- •7.1 Дроссельные расходомеры и труба Вентури
- •7.2 Измерение скорости и расхода жидкости с помощью трубок скоростного напора
- •7.3 Кавитация
- •7.4 Гидравлический удар в трубопроводах
- •8 Струйное движение
- •25.Некоторые понятия теории гидродинамического пограничного слоя
- •8.2 Элементы струйного движения
- •26.Аэродинамика свободной затопленной турбулентной струи
- •27.Струя во встречном и спутном потоках
- •28. Струя, ограниченная параллельной плоскостью
- •29. Рисунок 8.7 - Схема струи, ограниченной параллельной плоскостью Струя, атакующая поверхность под углом
- •30.Струя, втекающая в полость. Струйный аппарат
- •31.Взаимодействие свободных струй
- •9 Экспериментальные исследования гидродинамических процессов
- •32.Задачи исследований. Гидравлическое моделирование и теория подобия
- •33.Основы теории подобия
- •34.Способы получения критериев подобия
- •35. Метод масштабных преобразований
- •35.1. Метод анализа размерностей
- •36. Метод гидравлического моделирования
- •37. Расчет модели
- •38.Технические примеры моделирования.
- •10 Движение многофазных сред
- •39.Общие понятия
- •40.Потери давления при движении пароводяных смесей.
- •41.Контур естественной циркуляции
3.Равновесие несжимаемой жидкости под действием сил тяжести
Рассмотрим простейший случай равновесия неподвижной массы несжимаемой жидкости, находящейся под воздействием только сил тяжести, ускорение которой направлено вертикально вниз. Если координатную ось направить вниз, то в уравнении (2.4) компоненты ускорения массовых сил Х=Y=0, а Z=g и дифференциальное уравнение статики примет вид
Рисунок
2.3. К выводу основного уравнения
гидростатики

Если полагать, что свободная поверхность (рис. 2.3) имеет координату z0 и на этой поверхности внешнее давление равно p0 (в частном случае это давление может быть равно атмосферному ратм), то, интегрируя уравнение (2.6) в пределах от z0 до z и от р0 до р получим, при условии =const
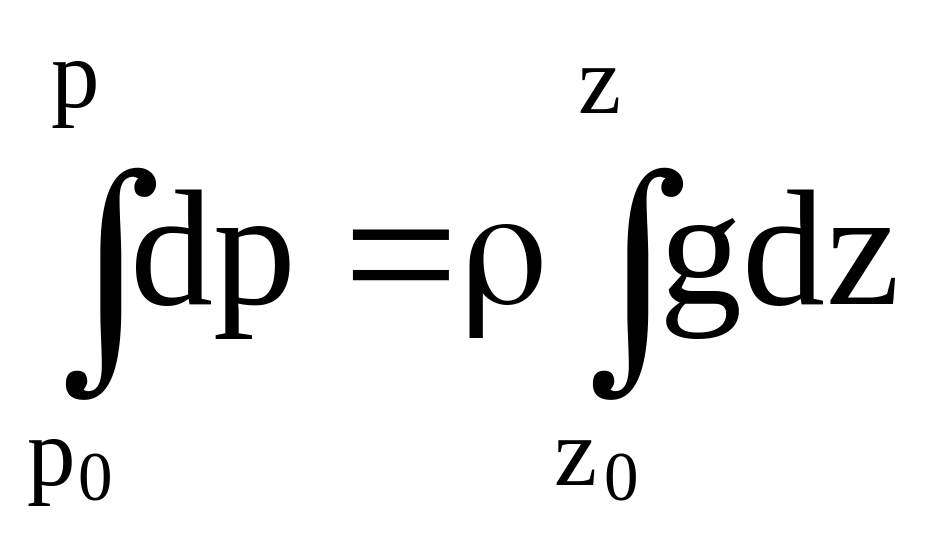
р = р0+g(zz0) . (2.7)
Если начало координатной оси Оz совместить с уровнем свободной поверхности, тогда z0=0 и уравнение (2.7) примет вид:
p = p0+gz. (2.8)
Это выражение называется основным законом гидростатики: давление в любой точке покоящейся жидкости равно внешнему давлению (р0), сложенному с весом столба жидкости высотой от поверхности до данной точки и с площадью основания, равной единице.
Если в выражении (2.4) положить p=const, или dp=0, то получим уравнение поверхности уровня
Xdx+Ydy+Zdz = 0, или dU=0, (2.9)
следовательно поверхность уровня является и поверхностью равного потенциала, или эквипотенциальной поверхностью. Какова форма поверхности уровня для жидкости, находящейся под действием только сил тяжести? Чтобы ответить на этот вопрос положим p=const, тогда уравнение поверхности (2.9) примет вид:
![]()
т.е. поверхностью уровня является горизонтальная плоскость.
4.Равновесие несжимаемой жидкости при наличии негравитационных массовых сил
4.1.Равноускоренное движение жидкости в горизонтальном направлении
Рассмотрим движение жидкости в некотором сосуде (например, в цистерне) с горизонтальным ускорением a; жидкость находится под воздействием инерционной силы, а также под действием силы тяжести с ускорением g (рис. 2.4). Если координатную ось Ох направить горизонтально по ходу движения, а ось Оz вертикально вниз, то в проекции ускорения массовых сил в уравнении (2.4) будут иметь место следующие значения:
X=a; Y=0: Z=g,
а основное дифференциальное уравнение статики примет вид:
dp = (adx+gdz).
Рисунок
2.4 Равновесие жидкости при равноускоренном
горизонтальном движении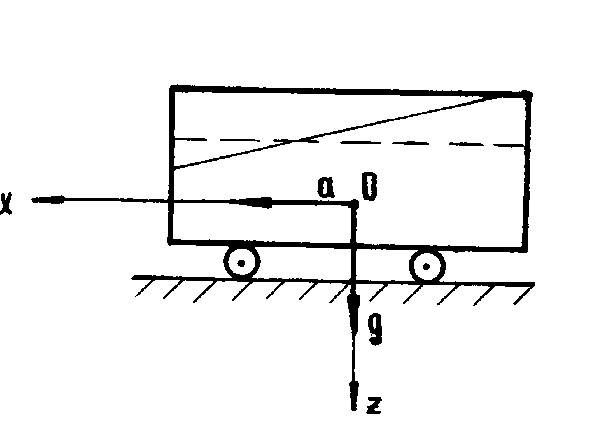
p = ax+gz+C.
Константа интегрирования определяется из условия: х=x0; z=z0; p=p0, следовательно, зависимость давления от координат будет иметь вид:
p = p0+a(xx0)+g(zz0) (2.10)
Для того, чтобы определить форму поверхности уровня, положим p=const. Тогда уравнение (2.9) может быть преобразовано к выражению типа
z = A + Bx, (2.11)
т.е. к уравнению прямой наклонной линии. Следовательно, в данном примере поверхностью уровня является наклонная плоскость.
4.2.Равновесие жидкости, покоящейся относительно сосуда и вращающейся относительно вертикальной оси
Пусть жидкость, находящаяся в сосуде, вращается вместе с сосудом относительно вертикальной оси с угловой скоростью (рис. 2.5). На покоящуюся относительно сосуда жидкость будут действовать центробежные силы и силы тяжести. Если расположить координатные оси Ох и 0y в горизонтальной плоскости, а ось направить вертикально вниз, то проекции ускорения центробежных сил будут равны (в соответствии с теорией вращательного движения): X=2x, Y=2y, а ускорение силы тяжести Z=g. Тогда основное дифференциальное уравнение статики (2.4) примет вид:
dp = (2xdx+2ydy+gdz).
После интегрирования получим
![]()
Рисунок
2.5 Равновесие жидкости, вращающейся
вокруг вертикальной оси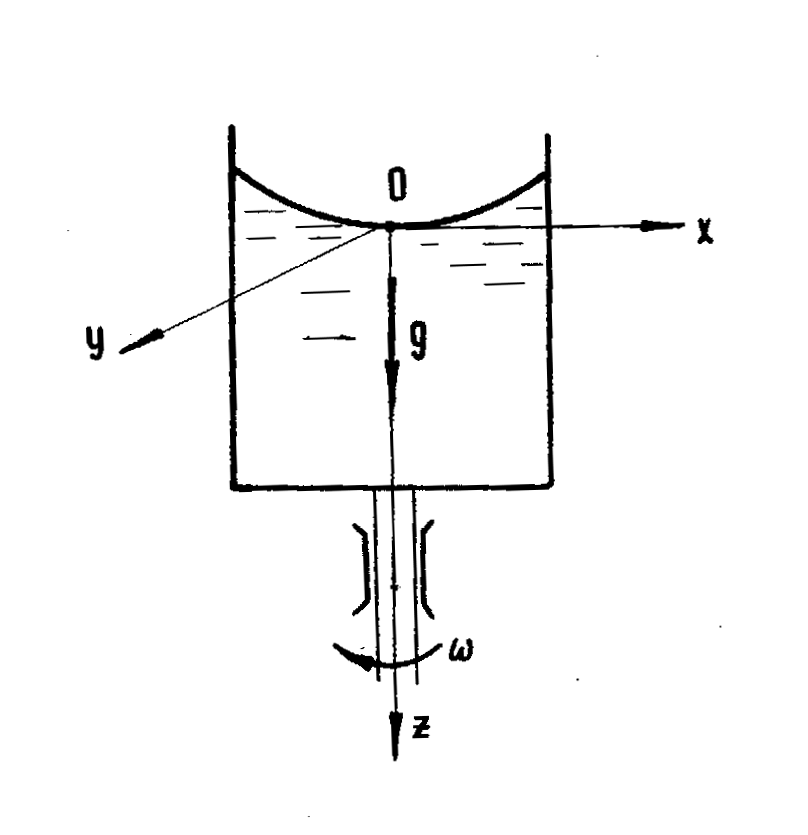
C=p0+gz,
а зависимость давления от координат будет иметь вид:
![]() . (2.12)
. (2.12)
Поверхность уровня (p=const) находится после преобразования (2. 12) к виду:
![]() (2.12)
(2.12)
(в константу С1 вошли все постоянные величины). Выражение (2.13) представляет собой уравнение параболоида вращения.
