37. Расчет модели

Расчету модели предшествует выбор моделирующего агента, а также геометрического масштаба модели. В качестве моделирующего агента выбирают воздух или воду в зависимости от того, какие задачи ставят перед исследованием: если нужно представить только картину движения, используют воду, если нужно получить численные значения скоростей и давлений в объеме модели, используют воздух. Выбор геометрического масштаба модели, т.е. отношение линейных размеров модели и образца, приводится с учетом удобства работы с моделью, а также возможностей лаборатории по расходу и давлению воздуха (воды).

После выбора масштаба модели приступают к расчету расхода моделирующего агента. Как правило, моделируют гидрогазодинамические процессы в рабочих камерах промтеплоэнергетических установок (напр., топка котла; рабочее пространство печи, и т.д.), в которых наблюдается сложное многомерное движение, называемое струйным, и которое формируется под действием одной или нескольких струй (напр., горелок). Иногда моделируют потоки внутри горелок, такие, как газовое топливо, распыленное жидкое топливо, первичный воздух, вторичный воздух. В зависимости от количества входящих в объект потоков модель может быть однопоточной или многопоточной.

Расчет однопоточной модели основан на равенстве определяющих критериев в модели и образце, которыми, как правило, бывают числа Рейнольдса:

Re' = M_ReRe (9.21)

где Re' и Re  соответственно число в моделе и образце ;

M_Re  масштаб чисел Рейнольдса. Принимают M_Re=1 ,если модель и образец неавтомодельны, и M_Re1 ,если они автомодельны. Дальнейший вывод достаточно прост:

, (9.22)

где w',w  скорость в сходственных сечениях модели и образца, м/с;

d',d  сходные линейные размеры, м;

,  коэффициенты кинематической вязкости моделирующей жидкости и жидкости в образце, м²/c.

Подставив вместо скорости отношение

,

(V объемный расход, м³/с; f  сечение, м²),получим

откуда расход моделирующего агента

где отношений  масштаб кинематической вязкости, d'/d = M  линейный масштаб, f''/f = M_f  масштаб площадей. Т.к. M_f = M² , окончательно получим:

V' = VM_ReM_Me. (9.23)

Расчет многопоточной модели состоит из двух этапов: 1)расчета общего расхода моделирующего агента, и 2) расчета распределения моделирующего агента по потокам. Первая часть расчета выполняется как для однопоточной модели. В основе второй части лежит соблюдение соотношения количеств движения потоков в модели и образце:

I'₁:I'₂:I'₃ ... = I₁:I₂:I₃ (9.24)

Например, для двухпоточной модели расходы по потокам определяются из системы уравнений

(9.25)

(9.26)

где I'₁,I' ₂ количество движения первого и второго потоков на модели;

I₁,I₂  то же на образце;

V'₁,V'₂  объемные расходы моделирующих агентов по первому и второму потокам;

V'  общий расход.

Количество движения можно выразить следующим образом

, (9.27)

где m  массовый расход ,кг/с,

V  объемный расход ,м³/с,

  плотность, кг/м³.

Отношение количеств движений

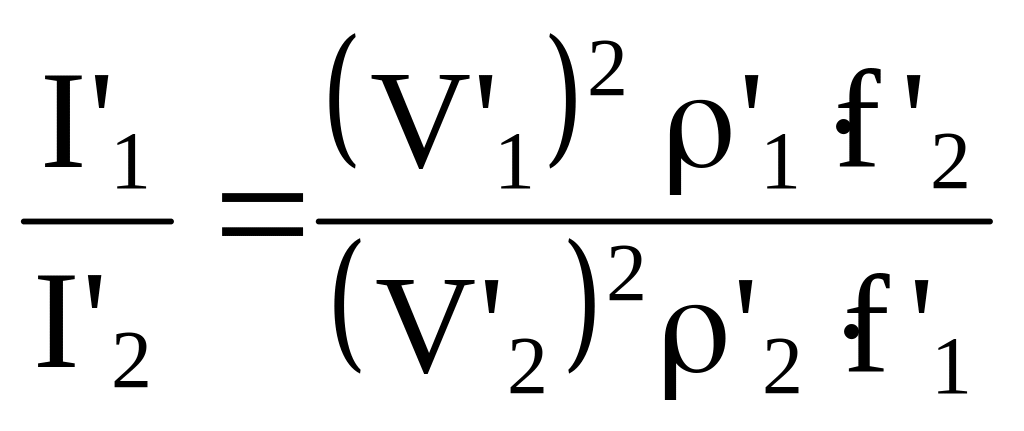. (9.28)

Подставив (9.28) в (9.26), получим

. (9.29)

Т.к. из (9.25)

V'₂=V'V'₁

то

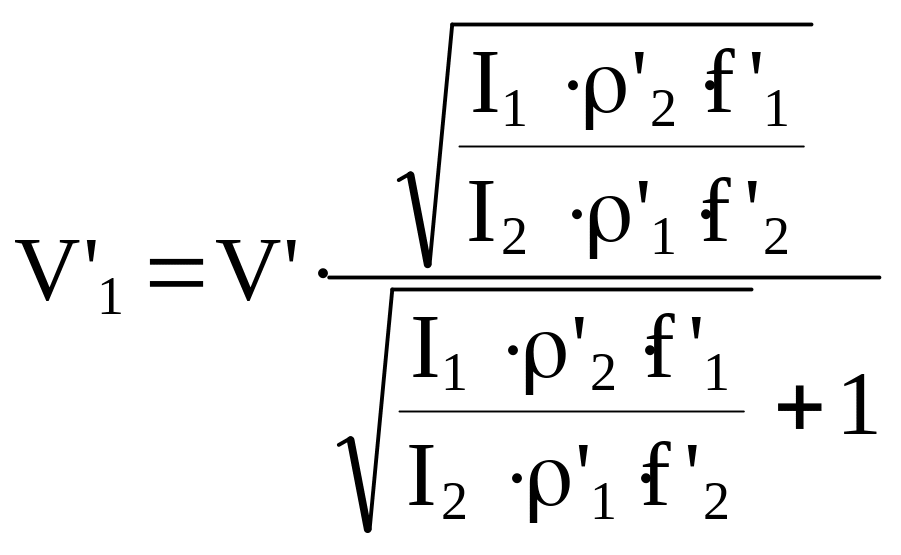. (9.30)

Таким образом, расходы моделирующих агентов определяются по выражениям (9.29) и (9.30).

Пересчет экспериментальных данных с модели на образец производится через масштабы скорости M_W и давление M_p. Масштаб скорости может быть получен из (9.22):

. (9.31)

Масштаб давлений (точнее, перепадов давлений) для турбулентной области течения выводится из квадратичной зависимости гидравлического сопротивления от скорости:

.

Масштаб давлений

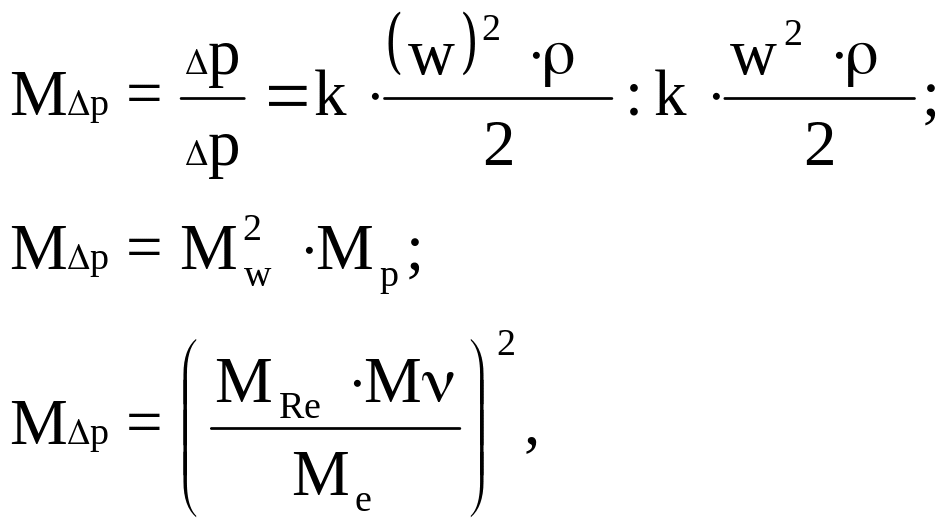(9.32)

(коэффициенты сопротивления k' и k равны, т.к. модель и образец геометрически подобны).

Таким образом, скорость жидкости пересчитывается с модели на образец по формуле:

(9.33)

а перепад давлений между двумя точками образца по формуле:

, (9.34)

где w' и p'  экспериментальные данные по скорости и перепаду давлений, полученные в модели.

Пример расчета модели приведен в приложении 9.