7 Применение уравнения бернулли в технических устройствах и расчетах

7.1 Дроссельные расходомеры и труба Вентури

Рисунок 7.1 - Cхемы дроссельных расходомеров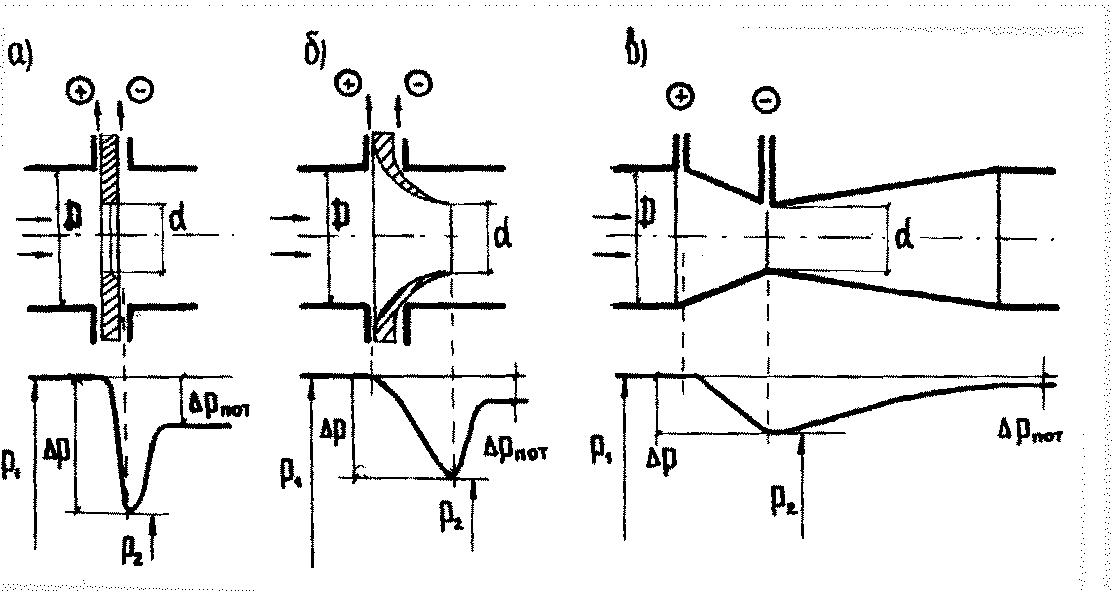

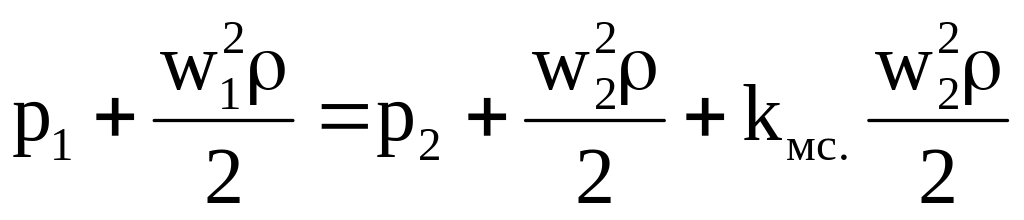Один из способов измерения расхода жидкости в трубопроводе основан на связи изменения статического давления в дроссельном (сужающем) устройстве со скоростью потока: w = f(p) (дросселирование  это процесс понижения давления в потоке). В качестве измерительных устройств применяют диафрагмы (рисунок 7.1, а), сопла (рисунок 7.1, б ), трубы Вентури (рисунок 7.1, в). Измерение расхода основано на использовании уравнения Бернулли, записанного для сечений до и после сужающего устройства:

• . (7.1)

Разница статических давлений р₁  р₂ = р измеряется дифференциальным манометром, на « + » которого подается давление p₁, а на «»  давление p₂. Отношение сечений в сужающем устройстве, равное (d/D)² = m называется модулем, а отношение скоростей w₁/w₂=f₂/f₁=m в соответствии с законом сплошности. После подстановки «m» в (7.1) получим:

• ,

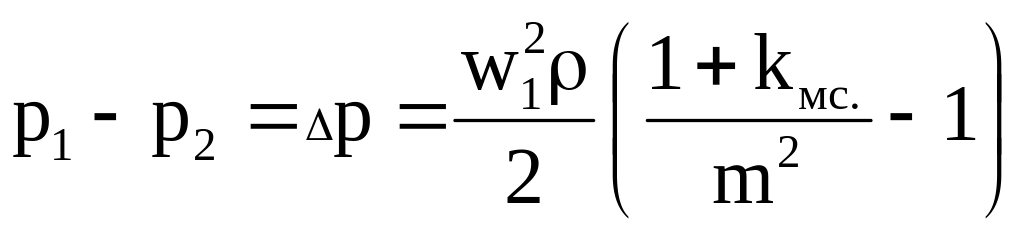откуда скорость перед сужающим устройством равна

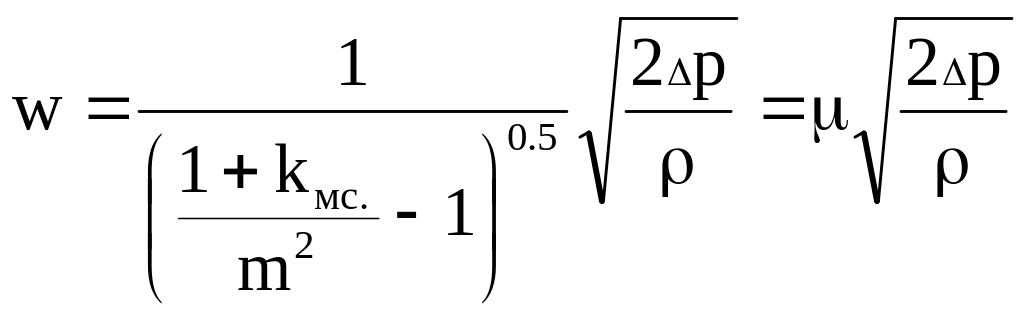• , (7.2)

а расход жидкости

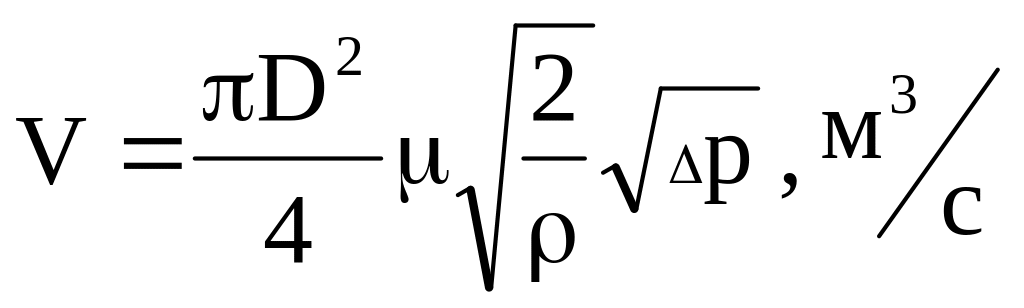• . (7.3)

Коэффициент сопротивления k_.мс. зависит от модуля «m» и вида сужающего устройства. Следует заметить, что наибольший перепад статических давлений в измерительном устройстве р и безвозвратные потери р_пот наблюдаются для диафрагмы, наименьшие  для трубы Вентури. Так, для m=0,5 потери составляют для диафрагмы 46, сопла 28 и трубы Вентури 6% от перепада давления. Однако диафрагмы, несмотря на большие энергетические затраты, на практике встречаются чаще, т.к. являются наиболее простыми, удобными и точными приборами.

7.2 Измерение скорости и расхода жидкости с помощью трубок скоростного напора

Французский ученый Анри Пито в 1732 году применил трубку полного напора (полая стеклянная трубка с загнутым концом) для измерения скорости воды в р. Сене, т.е. в канале с открытой поверхностью (рисунок 7.2,а). Жидкость в трубке, загнутый конец которой направлен навстречу потока, поднимается на высоту h_полн, причем часть её поднимается выше свободной поверхности воды. Статический напор в этом случае  это гидростатический напор, равный глубине погружения трубки, а т.к. h_полн=h_ст+h_дин, то высота подъёма жидкости над поверхностью равна динамическому или скоростному напору. Т.к. динамический напор и скорость связаны квадратичной зависимостью, то измерив скоростной напор можно рассчитать и скорость:

• .

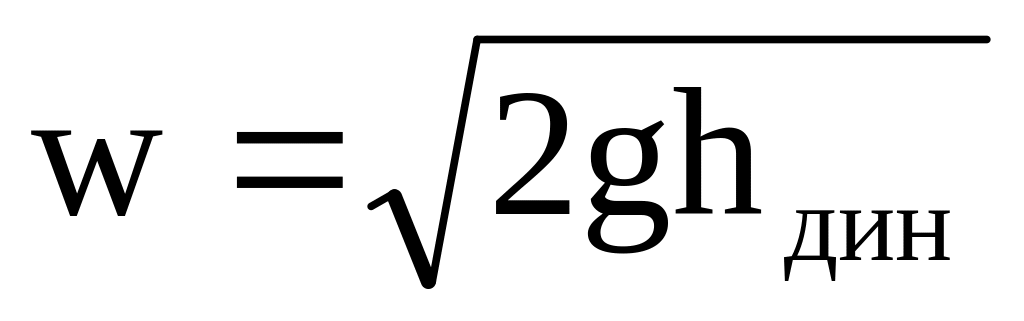Рисунок 7.2 - Принцип действия трубок полного и скоростного напора

Однако такой способ не применим для измерения скорости в закрытом напорном канале или трубопроводе. Немецкий ученый Людвиг Прандтль предложил усовершенствовать трубку Пито и измерять динамическое давление с помощью двух трубок (рисунок 7.2, б), и разность полного и статического давлений, равная динамическому давлению, измеряется дифференциальным манометром. Такие устройства называются трубками Пито  Прандтля. Скорость потока рассчитывается по формуле:

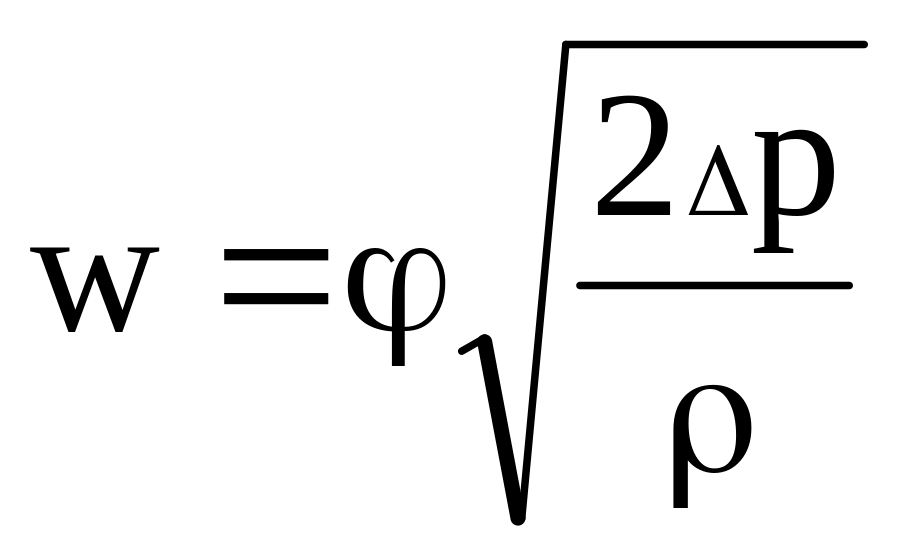• (7.4)

где   тарировочный коэффициент зонда, определяемый экспериментально в аэродинамической трубе.

7.3 Кавитация

• На участке некоторых местных сопротивлений скорость потока жидкости (капельной) резко возрастает, статическое давление падает и, если оно становится ниже давления насыщения паров р_нп, то возникает местное закипание при низких температурах. Это явление называется кавитацией; оно сопровождается вибрацией и сильным шумом. Кавитация нарушает нормальную работу оборудования, а возникающая при этом эрозия приводит к разрушению материала. При наличии кавитации заметно возрастают потери энергии на местные сопротивления.

• При гидравлических расчетах трубопроводов необходимо обеспечить бескавитационную работу, выбирая максимальные скорости меньше критических значений, определяемых по формуле:

• ,

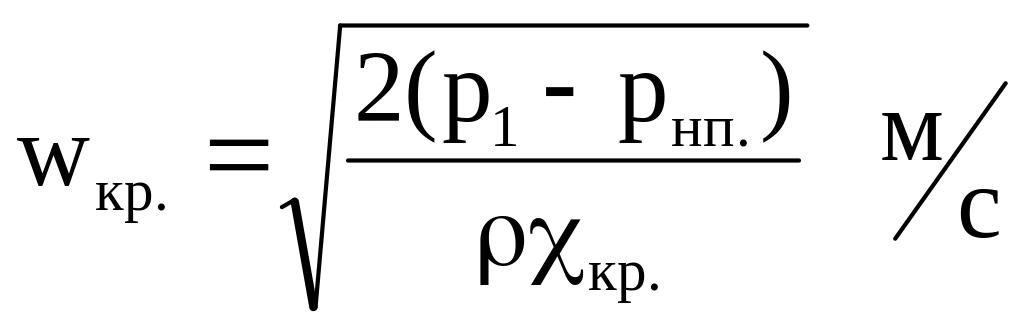• где p₁  давление жидкости перед местным сопротивлением, Па;

• р_нп  давление насыщенного пара при данной температуре, Па;

• _кр  критическое число кавитации, зависящее от коэффициента местного сопротивления и определяемое по справочнику.

• Кавитация наблюдается также у поверхности лопаток, гребных лопастей, подводных крыльев и др. Эрозия материала, возникающая при кавитации, наиболее развита в замкнутых областях, в которых пузырьки пара накапливаются; и менее развита, если кавитацию направить в "бесконечность", т.е. обеспечить срыв пузырьков пара с лопастей, что можно получить, если использовать рациональную форму лопаток.