5 Гидравлические расчеты промышленных газоходов и трубопроводов

17.Уравнение Бернулли для потока реальной жидкости

Полученное выше уравнение Бернулли для идеальной жидкости (4.9) строго применимо лишь для элементарной струйки или трубки тока, в пределах которой скорость одинакова по сечению. Если рассматривать поток жидкости как совокупность элементарных струек, то в поперечном сечении потока будет наблюдаться неравномерное поле скоростей, и уравнение Бернулли запишется в виде

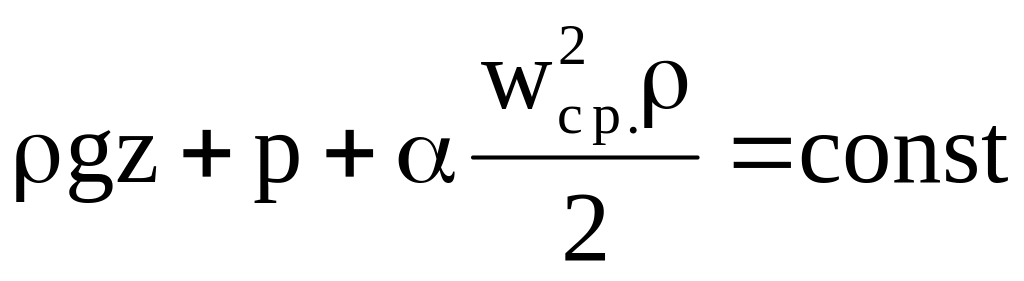• , (5.1)

• где w_cp  среднее по сечению потока значение скорости, определяемое как отношение объемного расхода к площади поперечного сечения;

•   коэффициент Кориолиса, учитывающий неравномерность распределения скоростей. Коэффициент Кориолиса в общем случае зависит от режима течения, числа Рейнольдса, диаметра трубопровода (D), шероховатости стенок (). Для ламинарного режима =2. Для турбулентного режима  = 1+2,65, где  = f(Re, /D)  коэффициент трения стенок трубопровода; для этого режима 1,0 << 1,15, и часто в расчетах трубопровода, особенно большого диаметра, коэффициент Кориолиса принимают равным единице.

При движении реальной жидкости возникают потери энергии на преодоление сопротивления трубопровода, поэтому уравнение Бернулли, записанное для двух последовательных сечений, имеет вид:

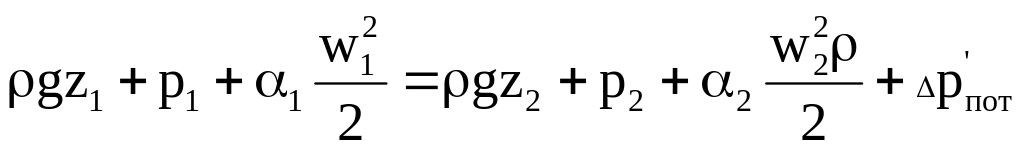• (5.2)

18.Уравнение Бернулли в избыточных давлениях

В гидравлических расчетах газоходов, трубопроводов, систем удаления продуктов горения и т.д. обычно пользуются уравнением Бернулли, записанным для избыточных давлений, представляющих собой разность между давлением в потоке и атмосферным давлением на том же уровне. Если для развитого турбулентного потока принять коэффициент Кориолиса равным единице, то уравнение Бернулли в абсолютных давлениях для двух сечений канала (рис. 23) запишется в виде:

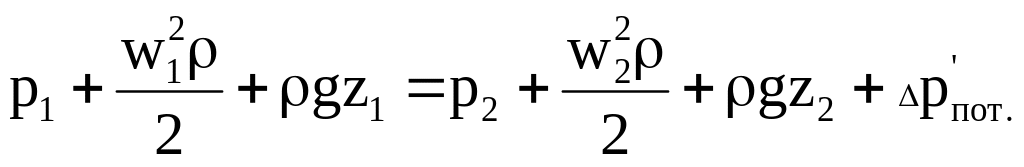• . (5.3)

Давление атмосферы (окружающего воздуха) на уровне z₁ и z₂ связаны законом гидростатики:

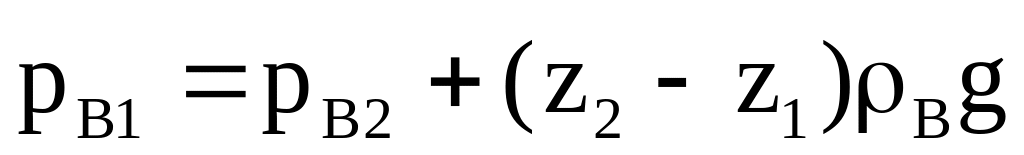• . (5.4)

Рисунок 23. К выводу уравнения Бернулли в избыточных давлениях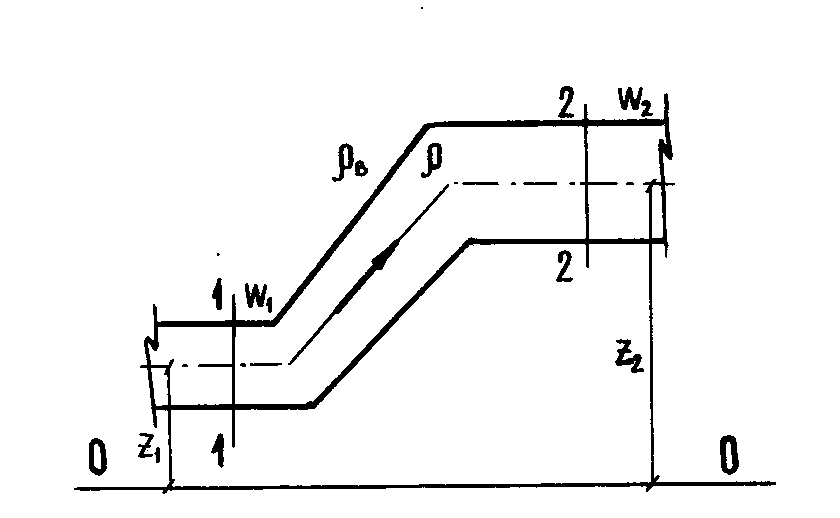

Равенство (5.3) не нарушится, если из левой его части вычесть левую часть уравнения (5.4), а из правой  правую часть уравнения (5.4). После преобразований получим:

. (5.5)

Выражение в скобках p₁  p_в1 есть избыточное статическое давление в канале в сечении 1  1. Теперь уравнение Бернулли в избыточных давлениях примет вид

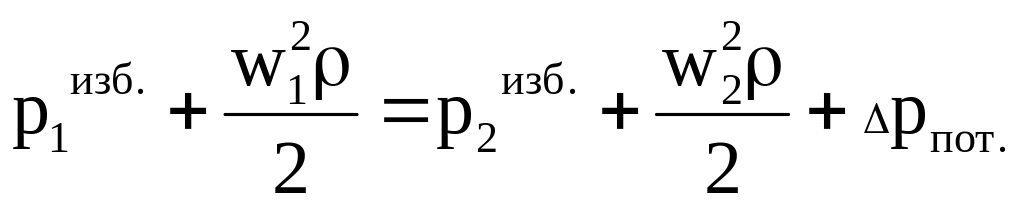• . (5.6)

• где р_пот = g(z₁z₂)(_в_г)+ р_пот = р_г+р_тр+р_м.с.  потери давления на участке между сечениями 11 и 22, состоящие из потерь геометрического давления р_г, потерь на трение р_тр, и потерь в местных сопротивлениях р_м.с.

19. Потери на трение

Потери давления на трение возникают при движении жидкости (газа) в трубопроводах (каналах), связаны с действием силы трения и представляют собой работу этой силы, отнесенную к единице объема жидкости. Расчет потерь на трение производится для прямых участков трубопроводов постоянного сечения.

19.1.Потери на трение в потоке несжимаемой жидкости

Потери давления на трение в потоке несжимаемой жидкости (p=const) определяют как величину, пропорциональную динамическому давлению:

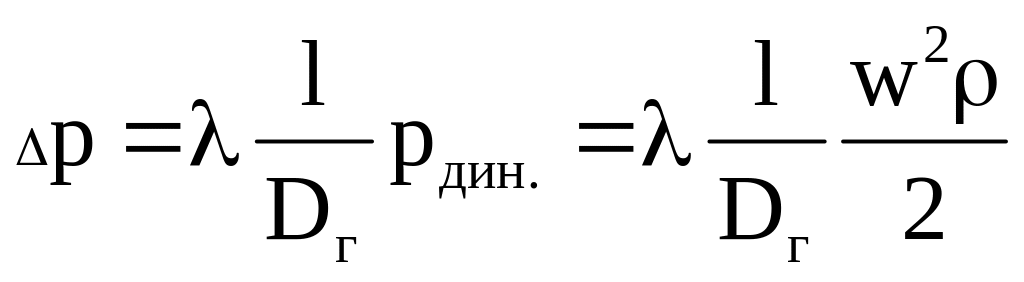• . (5.7)

Если скорость и плотность газа привести к нормальным физическим условиям:

• 

то выражение для динамического давления примет вид:

• ,

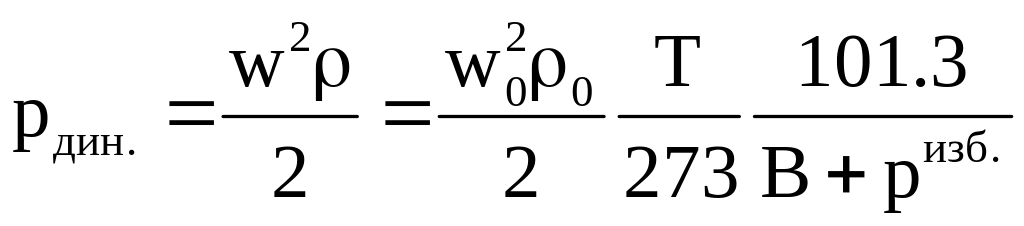а рабочая формула для расчета потерь на трение в потоке газа запишется в виде

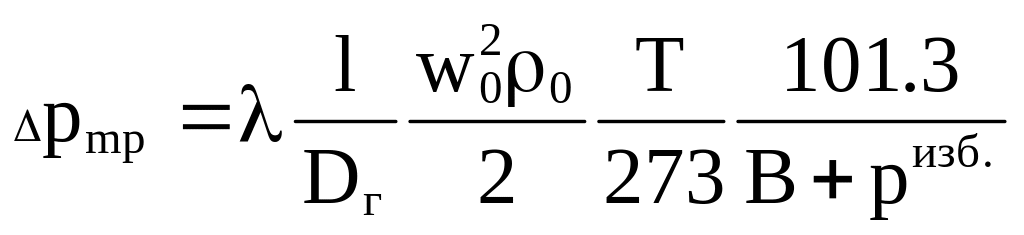• . (5.8)

В выражении (5.8):

• w_o  средняя скорость газа при н.ф.у., м/с;

• ₀  плотность газа при н.ф.у., кг/м³;

• Т  температура газа, К;

• В  барометрическое давление (атмосферы), кПа;

• р^изб  избыточное статическое давление в газопроводе, кПа;

• l  длина прямого участка трубопровода, м;

• D_г гидравлический диаметр поперечного сечения трубопровода, м; для круглого сечения D_г=D, для сечения другой формы D_г=4F/П где F  площадь сечения, м, П  периметр сечения, м;

•   гидравлический коэффициент трения.