16.Уравнение Бернулли для идеальной несжимаемой жидкости

• Рассмотрим стационарное движение элементарной струйки несжимаемой идеальной жидкости при условии, что компоненты скорости изменяются только в направлении соответствующих координатных осей. Если такое движение описать уравнениями движения Эйлера (4.1), то в первом из системы уравнении:

• 

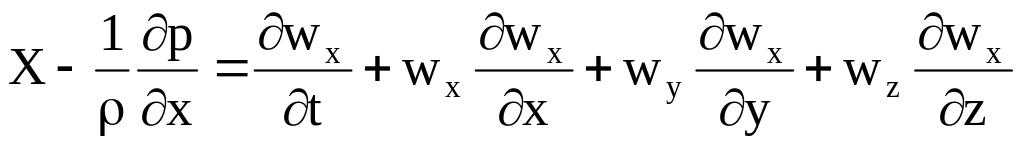
, т.к. движение стационарно, , т.к. нет изменения скорости по разноименным координатам. Аналогично упрощаются и другие уравнения, и система уравнений Эйлера принимает вид:

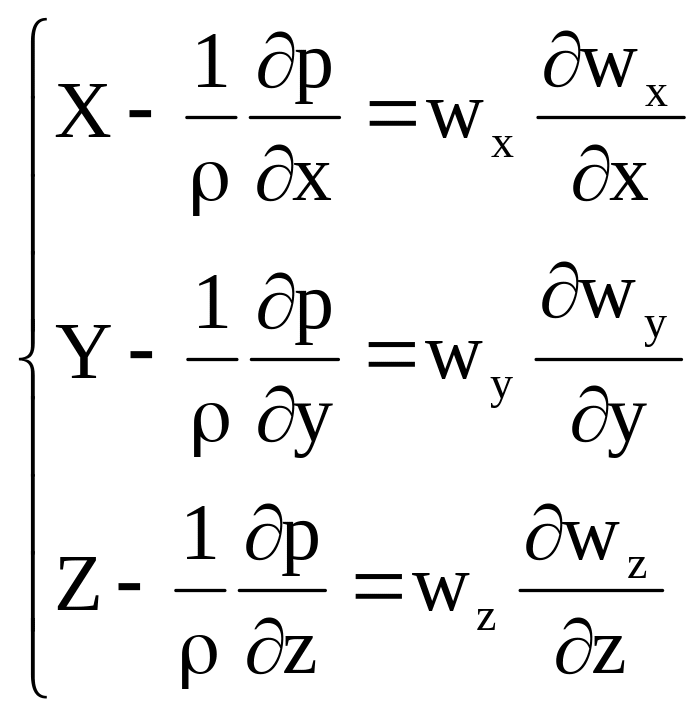• . (4.7)

Умножив первое уравнение на dx второе на dy третье на dz и просуммировав уравнения, получим:

• 

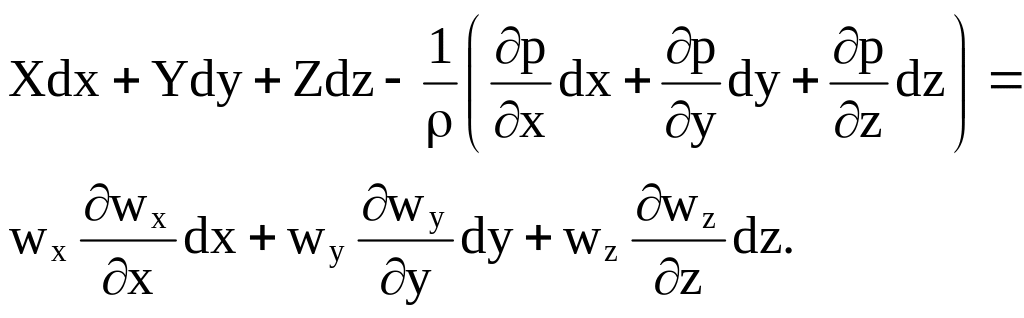
• Рассмотрим случай, когда из массовых сил действует только сила тяжести с ускорением, направленным вертикально вниз, и если координатную ось направить вертикально вверх, то Z= - g, Х=0, Y=0, и полученное выражение примет вид:

• 

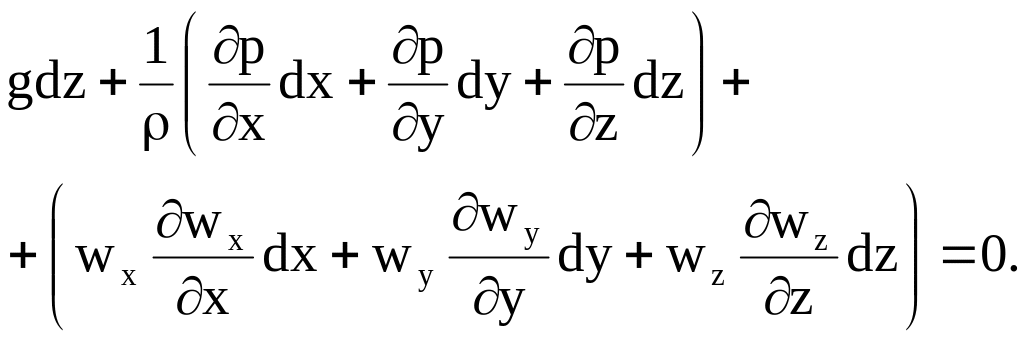
Выражение в первых скобках есть полный дифференциал давления:

• .

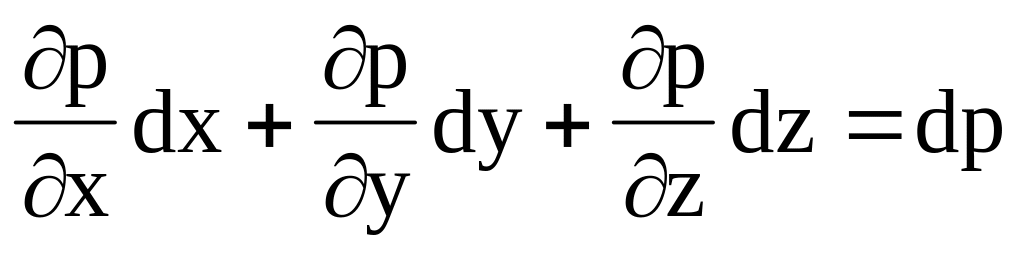Выражение во вторых скобках представляет собой полный дифференциал половины квадрата скорости

• .

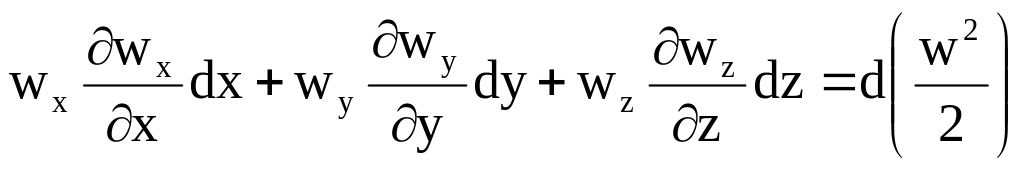Теперь уравнение примет вид:

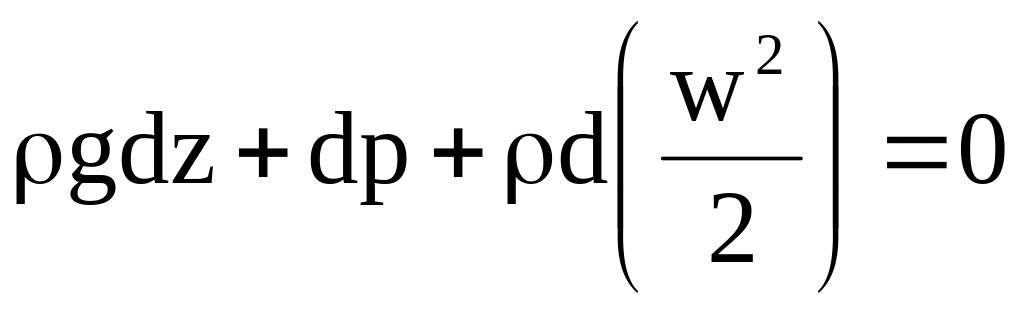• . (4.8)

Интегрируя это выражение, получим

(4.9)

Разделив все члены этого уравнения на g=, получим

• (4.10)

Уравнение (4.9) является уравнением Д. Бернулли в давлениях (получено в 1738 г.); уравнение (4.10) является уравнением Бернулли в напорах. Все члены второго уравнения называются напорами или высотами.

Уравнениям Бернулли можно дать геометрическое и энергетическое толкование. Геометрическую интерпретацию уравнения Бернулли в напорах составим на примере трубки тока переменного сечения и переменной высоты над некоторой начальной (нулевой) горизонтальной плоскостью отсчета высот (рисунок 4.2).

Рисунок 4.2 К геометрической интерпретации уравнения Бернулли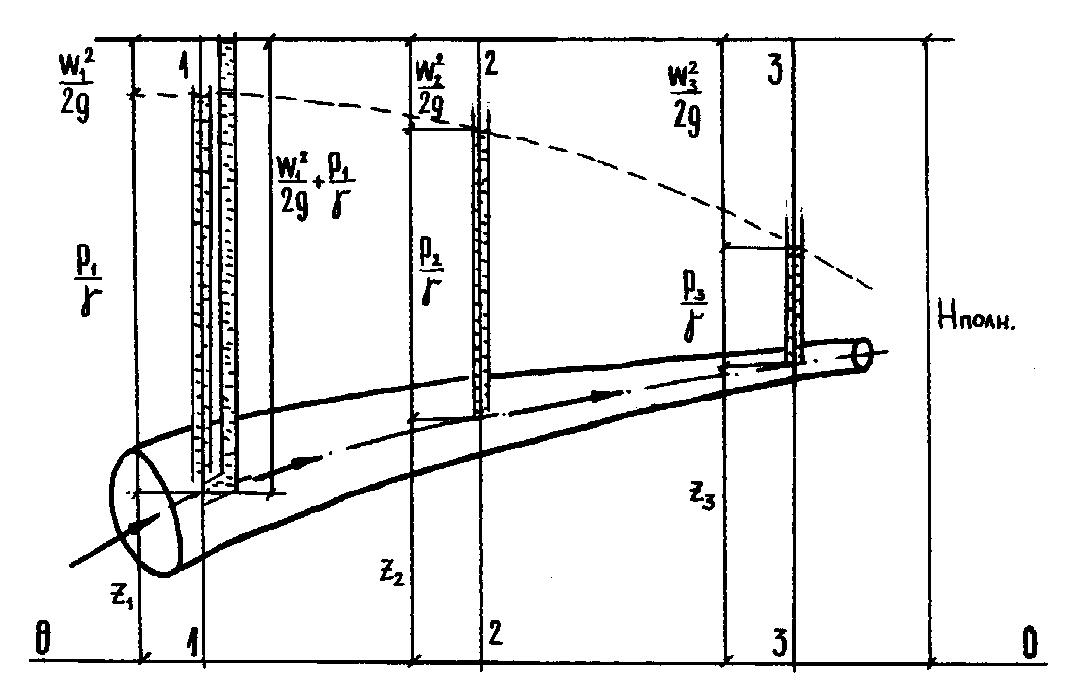

Рассмотрим три сечения по ходу движения жидкости: 1-1, 2-2 и 3-3. Первое слагаемое уравнения (4.10) z называется геометрической, или невелирной высотой (напором) и представляет собой положение точки над некоторой произвольно выбранной плоскостью; в нашем примере  это z₁, z₂ и z₃. Второе слагаемое p/ называется пьезометрической, или статической высотой (напором) и представляет собой высоту столба жидкости с удельным весом, уравновешивающим давление в данной точке. Эту высоту можно измерить с помощью тонкой стеклянной трубки, ось приемного отверстия которой совпадает с нормалью к направлению потока; жидкость поднимется по этой трубке на высоту, равную пьезометрическому напору, и в выбранных сечениях это будет  p₁/, p₂/, и p₃/. Третье слагаемое w²/(2g) называется динамической, или скоростной высотой (напором) и представляет собой высоту, с которой свободно падающее в пустоте тело достигнет скорости w. Эту высоту можно измерить с помощью двух тонких трубок, приемное отверстие одной из которых направлено навстречу потоку; эта трубка измеряет сумму пьезометрических и динамических высот вторая трубка измеряет пьезометрическую высоту. В нашем примере сечение трубки тока уменьшается в направлении движения, скорость соответственно увеличивается и динамическая высота увеличивается:

• 

Сумма всех трех слагаемых называется полной или гидравлической высотой (напором) и сохраняется постоянной во всех сечениях:

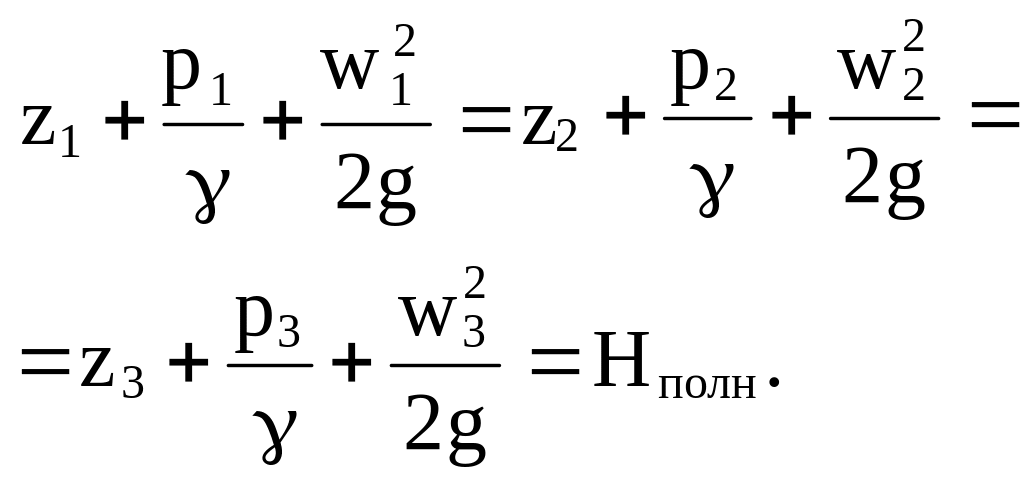• (4.11)

• Классической формулировкой теоремы Бернулли является следующая: при стационарном безвихревом движении несжимаемой идеальной жидкости полная (гидравлическая) высота, равная сумме пьезометрической, скоростной и геометрической высот, сохраняет постоянное значение во всей области течения.

• Уравнение Бернулли в давлениях (4.9) имеет энергетическое толкование. Оно может быть получено не только из уравнения Эйлера, но и другим путем. Рассмотрим в стационарно текущей идеальной жидкости трубку тока малого сечения (рисунок 4.3). За малый отрезок времени t жидкость переместится на l₁ в сечении 1-1 и на l₂. в сечении 2-2. Вследствие стационарности объемы V=s₁L и V=s₂l₂, равны, т.е. V₁=V₂=V. Энергия объемов V₁ и V₂ складывается из кинетической и потенциальной энергии

• .

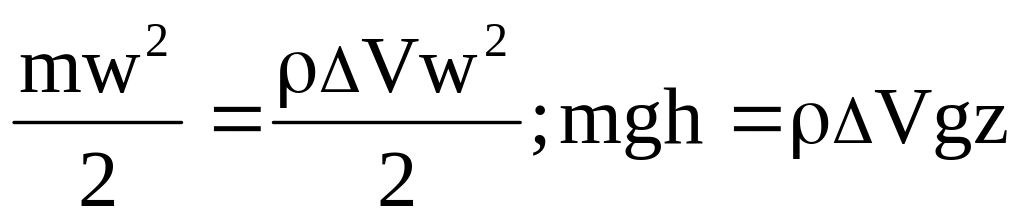Рисунок 4.3. К энергетической интерпретации уравнения Бернулли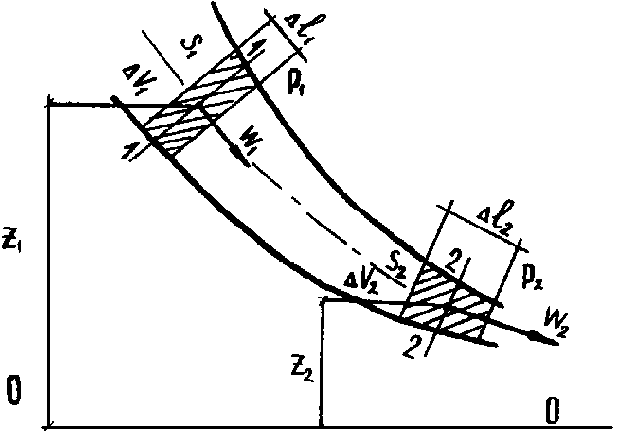

Приращение энергии E=E₂-E₁ равно:

• 

Т.к. в идеальной жидкости силы трения отсутствуют, то приращение энергии должно равняться работе, совершаемой силами давления над выделенным объемом:

• E=A=p₁s₁l₁-p₂s₂l₂=(p₁-p₂) V

Приравнивая правые части, перенося члены с одинаковыми индексами в одну сторону и сокращая на V, получим уравнение Бернулли:

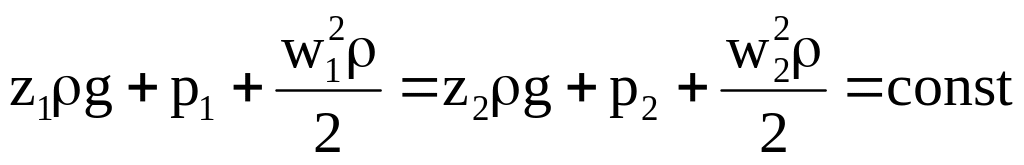• (4.12)

Т.к. все члены уравнения мы делили на объем, то следовательно все составляющие уравнения Бернулли являются энергиями, отнесенными к единице объема:

• gz  это энергия положения 1 м³ жидкости, называемая геометрическим давлением;

• p  это энергия давления 1 м³ жидкости, называемая статическим давлением;

• (p+gz)  потенциальная энергия 1 м³ жидкости;

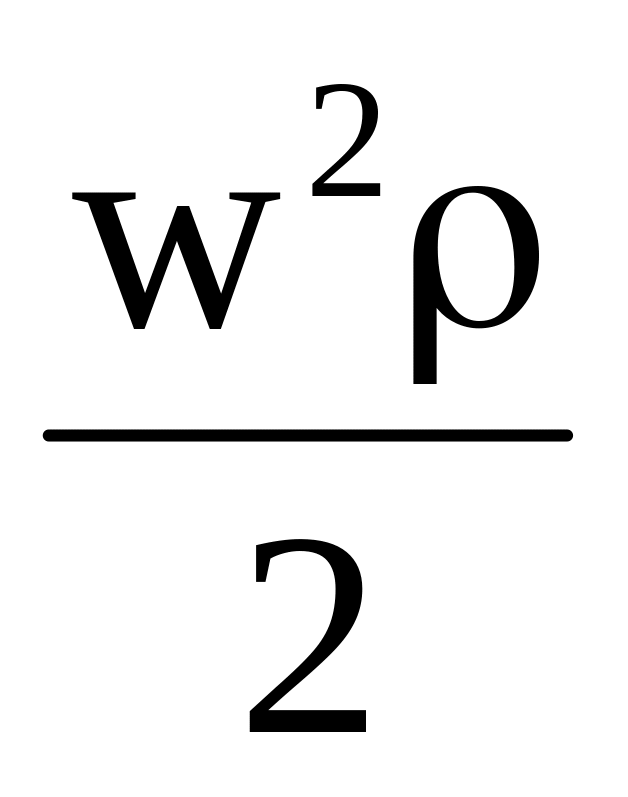•  это кинетическая энергия 1 м³ жидкости, называемая динамическим (скоростным) давлением.

• Уравнение Бернулли выражает собой закон сохранения энергии движущегося потока.