Постоянный ток

I = q сила тока

t

j = I плотность тока

S

I = U закон Ома для участка цепи

R

Закономерности при последовательном соединении проводников:

I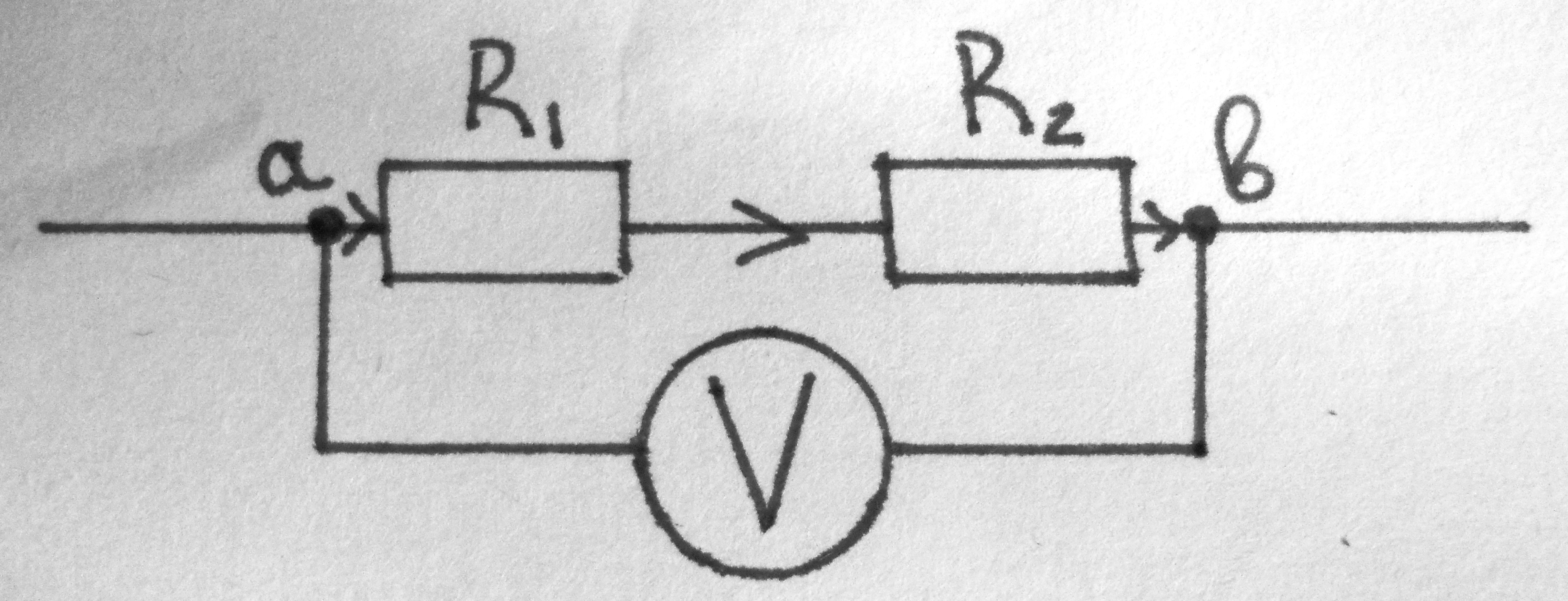 ₁ = I₂ = I₃

U = U₁ + U₂

R = R₁ + R₂ (R = nR₁)

U₁ = R₂

U₂ R₁

Закономерности параллельного соединения проводников:

I = I₁ + 2

U = U₁ = U₂

1 = 1 + 1 (R = R₁·R₂) (R = R₁)

R R₁ R₂ R₁+ R₂ n

I₁ = R₂

I₂ R₁

R = R₀[1 + α(t – t₀)] зависимость сопротивления Ме от температуры

A = P·t = q·U = U·I t = I²Rt = U² t работа тока

R

P = I·U = I²R = U² = A мощность тока

R t

Q = I²Rt = UI t = U² t закон Джоуля - Ленца для пост. тока

R

ε = A_стор. электродвижущая сила источника тока

q

(φ₁ – φ₂) = U = A_{элст 12} разность потенциалов между точками 1 и 2

q₊

U₁₂ = (A_эл12 + A_стор12) = φ₁ – φ₂ + ε₁₂ напряжение между точками 1 и 2 эл. цепи

q₊

I = ε закон Ома для полной цепи

R+r

U = I·R напряжение на внешнем участке цепи

U_i = I + r напряжение на внутреннем участке цепи

U ­­­+ U_i = ε сумма

I_кз = ε сила тока короткого замыкания источника тока

r

p = IU мощность, выделяющаяся на внешнем участке цепи

p_i = IU_i мощность, выделяющаяся на внутреннем участке цепи

p_∑ = p + p_i = I(U + U_i) = I ε мощность, выделяющаяся на всей цепи

η = p = U = R КПД источника тока

p_∑ ε R+r

I = n ε сила тока во внешн. цепи при последовательном соединении n

R+nr одинаковых источников тока

I = ε сила тока во внешн. цепи при параллельном соединении n

R+ r одинаковых источников тока

n

m = k I Δt закон электролиза

Магнетизм

B = F­_A определение индукции магнитного поля

I l sinα

F_A = I l B sinα закон Ампера

F_Л = qvB sinα модуль силы Лоренца

r = mv радиус кривизны траектории заряженной частицы, движущейся в МП

qB

T = 2Пm период обращения заряженной частицы, движущейся по окружности

qB в однородном МП

v = E условие равномерного прямолинейного движения заряженной частицы в

B скрещенных под прямым углом электрическом и магнитном полях

μ = B_∑ определение относительной магнитной проницаемости среды

B₀

Ф = Bscos α определение магнитного потока через плоскую поверхность,

находящуюся в однородном магнитном поле.

ε_i = — Ф' ЭДС индукции

ε_i = - Bvl sin α ЭДС индукции, индуцируемая в прямолинейном проводнике, движущемся в однородном магнитном поле под углом а к линиям поля

Ф_s = LI магнитный поток самоиндукции

L = Ф_s определение индуктивности проводника (контура)

I

ε_s = - LI ' ЭДС самоиндукции

W = LI² = Ф_sI = Ф_s² энергия магнитного поля

2 2 2L