3. Расчет на прочность по методу предельных состояний

Этот метод применяется, в основном, при расчете строительных конструкций.

Предельным называется такое состояние конструкции, при котором становится невозможной ее дальнейшая нормальная эксплуатация. В строительных нормах и правилах (СНиП) установлены три группы предельных состояний.

Первая группа предельных состояний определяется потерей несущей способности – прочности или устойчивости. Отличие от метода расчета на прочность по допускаемым напряжениям состоит в том, что применяется более гибкий подход к назначению необходимого запаса прочности. При этом вместо одного коэффициента запаса вводятся несколько:

• коэффициент надежности по нагрузке;

• коэффициент надежности по материалу;

• коэффициент условий работы.

Вторая группа предельных состояний определяется возникновением чрезмерно больших деформаций или колебаний. Предельные нормы часто не связаны с прочностью. Например, возникающие колебания и перемещения не приводят к разрушению, но вызывают дискомфорт у персонала или нарушают управляемость машинного агрегата. В СНиП такие нормы называют эстетико-психологическими.

Третья группа предельных состояний определяется образованием и развитием трещин. Обнаруженные трещины и другие дефекты, могут и не привести к потере выносливости. Важно оценить степень его опасности.

Различают три типа раскрытия трещин:

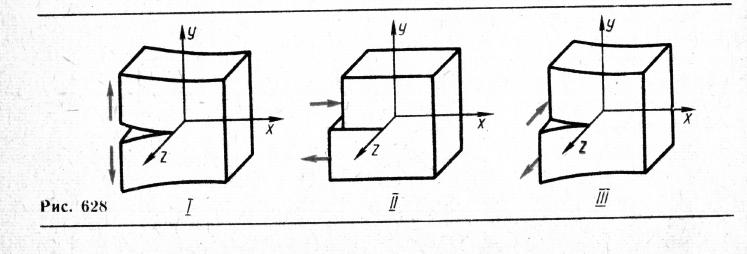
разрыв сдвиг срез

Рис.1

Выражения для коэффициентов интенсивности напряжений соответственно схемам нагружения:

, (2.17)

где l – половина длины трещины,

– номинальные нормальные и касательные напряжения в окрестности трещины.

При одинаковых коэффициентах интенсивности напряжений в различных телах с трещинами, поля напряжений у вершин трещин будут одинаковыми. Это обстоятельство позволяет рассматривать коэффициент интенсивности напряжений К_I как параметр, характеризующий напряжённое состояние у вершины трещины в зависимости от формы тела, размеров трещины, способа нагружения. Критические значения коэффициентов интенсивности напряжений K_Iс , K_IIс , K_IIIс определяют экспериментально. Методика их определения регламентируется соответствующими стандартами.

Условия роста трещин имеют вид:

K_I=K_Iс, K_II=K_IIс , K_IIс=K_IIIс (2.18)

4. Расчет на прочность по методу разрушающих нагрузок

Для конструкции, изготовленной из материала с достаточно большой площадкой текучести, за разрушающую принимают такую нагрузку, при которой в элементах конструкции возникают значительные пластические деформации. При этом конструкция становится неспособной воспринимать дальнейшее увеличение нагрузки. В ферме, например, это означает, что усилия во всех стержнях равны .

Для конструкции, изготовленной из хрупкого материала, за разрушающую принимается нагрузка, при которой хотя бы в одном из её элементов возникают напряжения, равные пределу прочности.

Исходя из этих принципов, производится расчет допускаемой нагрузки при заданном ее распределении, и вычисляется запас прочности.

3. Тексты заданий

1. Стержневые системы (задачи 1.1.1 …1.8.3)

Механические характеристики материала брать из таблицы 1 по указанию преподавателя.

Таблица 1 Механические характеристики материала

№ п/п	Е, МПа	μ	σТ, МПа	σВ, МПа	σ-1, МПа	σ0, МПа	Nб, цикл	m	К1С, КН/м3/2
1	2,2·105	0,32	960	1300	430	671	7·107	12	4·107
2	2,0·105	0,30	800	1100	380	590	2·107	8	13·107
3	2,0·105	0,35	700	1000	350	544	5·107	9	7·107
4	1,9·105	0,29	650	900	400	579	1·107	10	6·107
5	2,1·105	0,34	600	800	390	549	1·107	9	8·107
6	2,0·105	0,33	580	760	350	504	5·106	8	10·107
7	2,0·105	0,28	560	780	290	448	7·106	8	5·107
8	7,2·104	0,33	510	560	280	398	4·106	6	4·107
9	7,8·105	0,34	320	430	160	258	1·106	6	3·107
10	8,2·105	0,30	280	270	150	218	6·105	7	2·107

Определить запасы прочности при статическом нагружении:

1. по первой группе предельных состояний:

1. для фермы по прочности и устойчивости,

2. для сварной конструкции по прочности.

2. по разрушающей нагрузке:

1. для фермы из хрупкого материала,

2. для фермы из пластичного материала,

3. для сварной конструкции из хрупкого материала.

В задаче 1.1 критическую продольную силу в каждом стержне определять по формуле Эйлера для шарнирного закрепления, .

В задаче 2.2 пренебречь упрочнением. За запас прочности принять такое n, при котором нагрузка дает .

Варианты конструкций

Таблица 2

Сечение, Корд. узлов	Задача
	1			2			3			4
	Вариант			Вариант			Вариант			Вариант
	1	2	3	1	2	3	1	2	3	1	2	3
Сеч.	3х5	4,0	№5	3х6	6,0	№6,5	4х5	5,0	№8	3х5	4,0	№5
X1	-100	-150	-100	-100	-150	-100	0	0	0	0	0	0
Y1	0	0	0	0	0	0	0	0	0	0	0	0
X2	-100	-150	-100	-100	-150	-100	100	100	200	150	100	200
Y2	200	200	150	200	200	150	200	200	200	0	0	0
X3	0	0	0	0	0	0	200	200	250	150	100	200
Y3	200	200	150	100	100	75	0	0	0	-200	-200	-200
X4	100	150	100	100	150	100	250	350	300	300	200	200
Y4	0	0	0	0	0	0	200	200	200	0	0	0
X5	100	150	100	100	150	100	300	400	400	300	200	400
Y5	200	200	150	200	200	150	0	0	0	-200	-200	-200
Рx	100	200	150	100	200	150	120	150	200	100	200	150
Py	-100	-200	-150	100	200	150	-100	-100	-200	100	200	150
Сечение, Корд. узлов	Задача
	5			6			7			8
	Вариант			Вариант			Вариант			Вариант
	1	2	3	1	2	3	1	2	3	1	2	3
Сеч.	3х5	4,0	№5	3х6	6,0	№6,5	4х5	5,0	№8	3х5	4,0	№5
X1	0	0	0	0	0	0	0	0	0	0	0	0
Y1	0	0	0	0	0	0	500	500	500	500	500	500
X2	200	250	150	150	200	200	0	0	0	0	0	0
Y2	200	200	200	-200	-200	-200	400	400	400	400	400	400
X3	200	300	250	150	250	300	0	0	0	0	0	0
Y3	0	0	0	0	0	0	300	300	300	300	300	300
X4	300	350	350	200	300	400	0	0	0	200	300	300
Y4	200	200	200	-200	-250	-150	0	0	0	0	0	0
X5	400	450	450	300	300	400	300	250	350	200	300	300
Y5	0	0	0	0	0	0	400	300	500	400	300	400
Рx	100	200	150	100	-150	150	100	200	150	150	200	100
Py	-100	-200	-150	100	150	150	-100	-200	-150	-100	-200	100

Примечание: Размеры в см, силы в кН, сечения: прямоугольник, круг, швеллер