23

Физико-химические и теплофизические свойства сред, участвующих в процессах

1. Теоретические основы реологии

Переработка различных пищевых материалов сопровождается сложными физико-химическими, биологическими и механическими процессами, детальное изучение которых позволяет организовать объективный контроль и управление технологическим циклом производства. Особенности протекания этих процессов, конструктивные параметры рабочих органов соответствующих машин и аппаратов, а также качество получаемых продуктов питания в значительной степени зависят от реологических свойств перерабатываемых сред.

Реология - это наука о текучести и деформациях реальных сред. Системы уравнений, описывающие (при математическом моделировании) процессы переработки включают реологические (определяющие) уравнения, которые характеризуют связь скоростей деформаций с напряжениями. В реологические уравнения в качестве необходимого элемента входят реологические характеристики материала в виде констант или функций (вязкость, коэффициент консистентности, предел текучести, энергия активации вязкого течения и др.).

Реологические уравнения являются математическими моделями свойств реальных сред. Общий путь построения реологических уравнений состояния состоит в том, что ставится опыт или группа различных опытов, описывающихся теми или иными соотношениями. Затем эти соотношения обобщаются с помощью реологического уравнения состояния, и на основании полученного уравнения делаются предсказания относительно того, как материал будет себя вести в иных условиях эксперимента, отличных от изученных. Следующим этапом является экспериментальная проверка теоретических предсказаний.

Поскольку реологические методы дают однозначные физически значимые количественные оценки свойств среды, они коррелируют с ее структурой и могут использоваться для ее характеристики. Таким образом, реология предлагает также и методы контроля качества сред.

Основными процессами, в которых следует наиболее полно учитывать реологические свойства перерабатываемых сред, являются формование, перемешивание и транспортирование по трубопроводам. При изучении указанных процессов устанавливается взаимосвязь между реологическими характеристиками материала и технологическими параметрами его переработки.

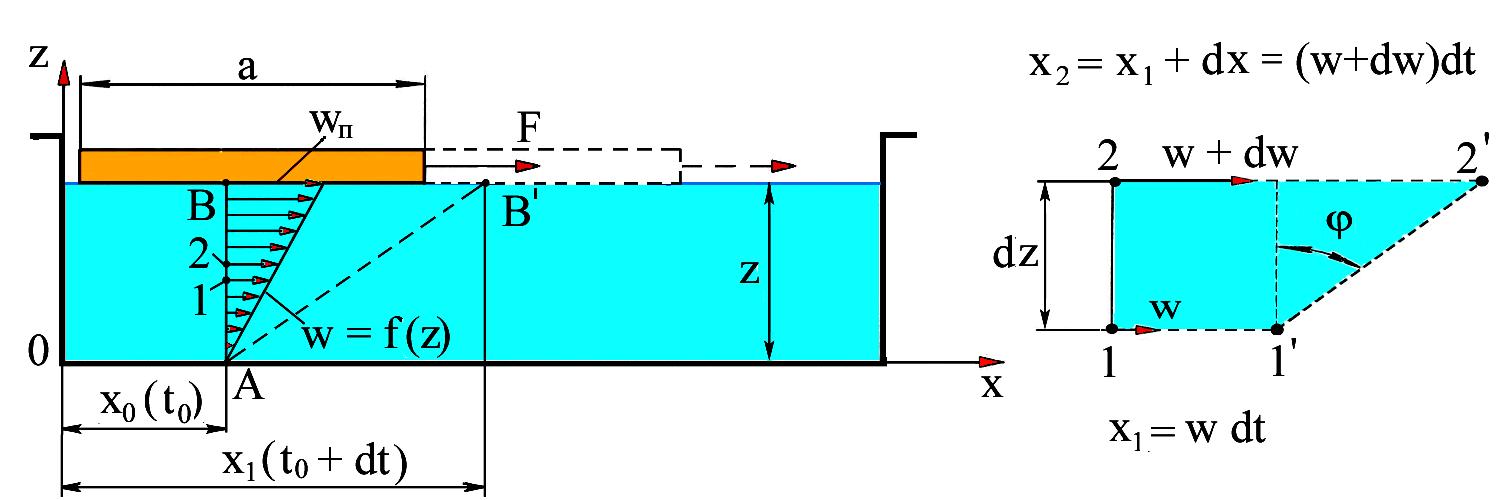
Рассмотрим под действием усилия F движение по поверхности жидкости пластинки, имеющей плотность, меньшую плотности жидкости (рис. 1.1, а). При движении пластинки со скоростью w_п ближайшие слои жидкости прилипают к ее поверхности и движутся вместе с ней, остальные слои смещаются друг относительно друга (рис. 1.1, б).

Согласно данной схеме величина относительного за время dt перемещения слоев, в плоскости которых лежат точки 1 и 2 составит:

Тогда скорость деформации сдвига представится соотношением:

(1.1)

а касательное напряжение (сила, приходящаяся на единицу площади пластины)

[Па], (1.2)

где а, в – размеры пластины в продольном и поперечном направлениях, м.

а б

Рис. 1.1. К формулировке закона Ньютона вязкого течения: а – расчетная схема движения пластинки по поверхности жидкости (----- – положение пластинки в момент t = t0 + dt); б – схема относительного перемещения слоев жидкости

По закону вязкого течения Ньютона сила касательного взаимодействия (касательное напряжение) между слоями жидкости пропорциональна приращению скорости одного слоя относительно другого, отнесенному к расстоянию между ними:

(1.3)

где μ₀ – ньютоновская вязкость (Па∙с) – физическая константа, характеризующая консистенцию среды, ее способность к течению (необратимому деформированию) и являющаяся мерой сопротивления перемещению одних слоев относительно других.

Жидкости, реологическое поведение которых подчиняется уравнению (1.3), носят название ньютоновских.

Общие методы теории абсолютных скоростей реакции, разработанные и перенесенные Эйрингом на диффузионные процессы и течение жидкостей приводят к следующему выражению зависимости вязкости от температуры:

(1.4)

где Е – энергия активации процесса, Дж/моль; Т – температура, К; A – постоянная, Па∙с.

Различают динамическую и кинематическую вязкости.

Динамическая вязкость – это вязкость в смысле Ньютона. Под кинематической вязкостью понимают величину, вычисляемую как

[м²/с]. (1.5)

В большинстве случаев реальные среды биотехнологической и пищевой промышленности относятся к неньютоновским жидкостям, у которых динамическая вязкость не является константой, а изменяется в зависимости от скорости сдвига и продолжительности деформирования в машинах и аппаратах. Зависимость для неньютоновских сред носит название кривой течения.

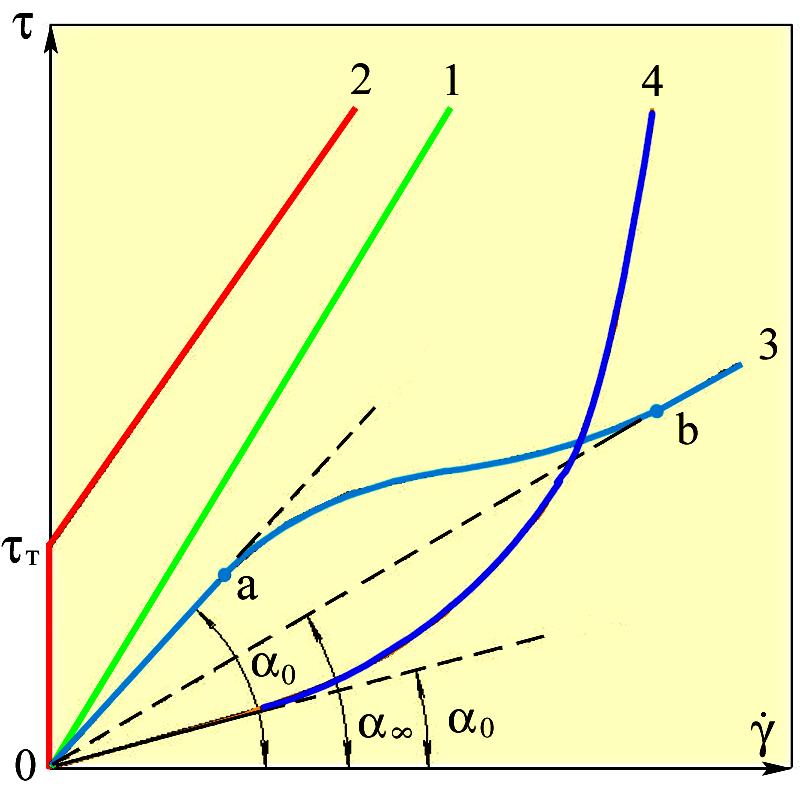
В зависимости от реологического поведения и вида кривой течения (рис. 1.2) указанные среды разделяют на следующие классы.

1. Ньютоновские (кривая 1): вода (μ₀ = 10^-3 Па∙с при 293 К); этиловый спирт (μ₀ = 1,25∙10 ^-3 Па∙с при 293 К), неконцентрированные суспензии (энтобактерин с μ₀ = 3,67∙10^-3 Па∙с при 293 К) и другие низкомолекулярные среды.

2. Бингамовские (кривая 2), особенностью которых является наличие предела текучести τ_т при независимости вязкости от скорости сдвига:

(1.6)

К ним относятся, например, шоколадные смеси, влажные пасты энтобактерина (τ_т = 9 Па, μ₀ = 0,2 Па∙с при влажности 89%).

Рис. 1.2. Кривые течения сред: 1 - ньютоновской; 2 – бингамовской; 3 – псевдопластичной; 4 – дилатантной

3. Псевдопластичные (кривая 3), обладающие начальной и конечной ньютоновскими вязкостями. Участку ab кривой течения отвечает эффективная (изменяющаяся) вязкость μ_эф, являющаяся функцией скорости сдвига.

Снижение динамической вязкости с ростом скорости сдвига объясняют тем, что в неподвижной среде расположение частиц характеризуется значительной хаотичностью. При росте скорости сдвига происходит все большая ориентация частиц в направлении течения, сопровождающаяся, кроме того, уменьшением взаимодействия между частицами. Отмеченные явления проходят в материале так быстро, что их нельзя проследить во времени в обычных приборах.

Для аналитического описания участка ab и зависимости эффективной вязкости от скорости сдвига применяют уравнение Оствальда:

(1.7)

где k – коэффициент консистентности; n < 1 – индекс течения.

Полностью кривую течения псевдопластичных сред позволяет описать, например, четырехконстантное уравнение Керри:

, (1.8)

где начальная и конечная ньютоновские вязкости, Па∙с; θ – характеристический коэффициент, с; n – индекс течения.

Свойство псевдопластичности проявляют влажные пасты энтобактерина, культуральные жидкости клубеньковых бактерий, томатные пасты, сахарные растворы, конфетные массы (для трюфельной массы «Экстра» k = 131 Па∙сⁿ; n = 0,31 при T = 298 К), крахмальные суспензии, майонез и ряд других сред.

4. Дилатантные (кривая 4), характеризующиеся ростом вязкости с повышением скорости сдвига. Это течение описывается уравнением Оствальда (1.7) при n > 1. Дилатантные материалы встречаются значительно реже, чем псевдопластические. Примером таких материалов могут служить сгущенное молоко, некоторые растворы кукурузной муки, сахара и крахмала.

5. Тиксотропные, имеющие зависимость вязкости не только от скорости сдвига, но и времени деформирования, что связано с разрушением имеющихся в материале структур. Материал считается тиксотропным, когда его вязкость снижается в течение времени деформирования, причем предполагается, что структура после определенного времени покоя возвращается к первоначальному состоянию. Время тиксотропного разрушения, так же как и восстановления, для различных сред изменяется в очень широких пределах. Примером тиксотропных пищевых материалов могут служить бараночное тесто, пралиновые и трюфельные конфетные массы, какао тертое, мясной фарш и др.

6. Реопектические, обладающие свойством упрочнения из-за возникновения с течением времени деформирования весьма сложных структур. Такие материалы, называемые также антитиксотропными, встречаются весьма редко.

7. Вязкоупругие (максвелловские) проявляют как вязкие (характеризуемые вязкостью μ₀), так и упругие (характеризуемые модулем упругости G₀) свойства. Если в упругом материале напряжение, соответствующее определенной деформации, не зависит от времени нагружения, то в вязко-упругой среде напряжение постепенно падает. С другой стороны, вязко-упругие материалы текут подобно чисто вязким жидкостям, но часть их деформации при снятии напряжения постепенно восстанавливается. Примерами вязкоупругих жидкостей являются полимеры, мучное тесто. Вязко-упругий эффект проявляется в «разбухании» (увеличении поперечных размеров) жгутов теста и конфетных масс при выходе из формующих отверстий прессов макаронного и конфетного производства. Это является результатом частичного восстановления материала благодаря эффекту упругого последействию.

Вязкость суспензий может быть вычислена по уравнению Муни, справедливому до объемных концентраций = 0,5…0,6:

, (2.9)

где φ_кр = 0,74 – критическая объемная концентрация дисперсной фазы, соответствующая предельно возможной степени заполнения объема сферическими частицами, что достигается при образовании ими гексагональной структуры; - вязкость дисперсионной фазы, Па∙с.

Вязкость смеси неассоциированных жидкостей вычисляют по формуле:

(1.10)

где μ₁, μ₂, μ₃… - вязкости отдельных компонентов; x₁, x₂, x₃…– мольные доли компонентов.

Вязкость газовых смесей вычисляют по приближенной формуле:

(1.11)

где μ₁, μ₂, μ₃… – вязкости отдельных компонентов; m₁, m₂, m₃…– объемные доли компонентов в смеси; M_гс = M₁x₁ + M₂x₂ + M₃x₃ + … - молекулярная масса смеси газов; M₁, M₂, M₃… – молекулярные массы компонентов.

Значения динамической вязкости и плотности некоторых пищевых сред, проявляющих как ньютоновское, так и нелинейное реологическое поведение приведены в табл. 1.

Таблица 2. Значения физико-механических характеристик некоторых пищевых сред

№ п/п	Нименование среды	Температура, °С	Динамическая вязкость, мПа∙с	Плотность, кг/м3
1	Молоко цельное	20	1,79	1029
2	Сметана с разрушенной структурой (20 %)	20	20…200	1004…1010
3	Кефир нежирный с разрушенной структурой	20	20…200	1028…1030
4	Йогурт с разрушенной структурой	20	20…200	1028…1030
4	Сливки (30 %)	20	5…10	1004
5	Простокваша с разрушенной структурой	20	20…200	1028…1030
6	Сахарный раствор (60 %)	20	64	1332
7	Осветленный виноградный сок (10 % СВ)	20	1,34	1,022
8	Осветленный яблочный сок (10 % СВ)	20	1,42	1042
9	Водно-спиртовой раствор (40%)	20	2,88	950