
- •Оглавление
- •Предисловие
- •1 Пространство элементарных исходов . Операции над событиями и отношения между событиями
- •2 Классическое определение вероятности, нахождение числа элементов в множествах комбинаторными методами. Геометрические вероятности
- •3 Теоремы сложения и умножения. Независимость событий. Вероятность наступления хотя бы одного события из нескольких независимых
- •4 Формулы полной вероятности и байеса
- •5 Схема бернулли
- •6 Приближенные формулы в схеме бернулли
- •7 Одномерные случайные величины
- •Важнейшие случайные величины
- •8 Многомерные случайные величины и их характеристики. Функции от случайных величин
- •9 Однородные цепи маркова (дискретное время)
- •10 Марковские процессы
- •11 Важнейшие процессы, моделирующие потоки событий
- •12 Предельный режим для марковских процессов
- •13 Важнейшие системы массового обслуживания, моделируемые марковскими процессами
- •7 Дискретные случайные величины
- •7 Непрерывные случайные величины
- •Приложение
7 Одномерные случайные величины
Рассмотрим
пространство элементарных исходов
некоторого испытания. Функция ,
определенная на элементах
и ставящая каждому элементарному исходу
некоторое число
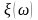 ,
называется случайной величиной. Функция
распределения
,
называется случайной величиной. Функция
распределения
 случайной величины ,
определяется равенством
случайной величины ,
определяется равенством
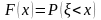 (7.1)
(7.1)
где х - действительное число (предполагается, что вероятность, стоящая справа в (7.1) определена при всех х). При решении задач часто используются следующие свойства функции распределения:
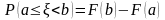 (7 .2)
(7 .2)
(при а < b). Полезны также следующие равенства:
 (7.3)
(7.3)
Случайная
величина
называется дискретной если она принимает
конечное или счетное число значений
 .
Дискретная случайная величина может
быть задана рядом распределения, который
можно представить в виде таблицы
.
Дискретная случайная величина может
быть задана рядом распределения, который
можно представить в виде таблицы
-
Значения
x1
x2
…
Вероятности
P1
P2
…
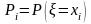
Для дискретной случайной величины выполняется равенство
 (7.4)
(7.4)
Случайная
величина
называется непрерывной, если существует
неотрицательная функция
 ,
удовлетворяющая при всех х
равенству
,
удовлетворяющая при всех х
равенству
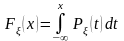 (7.5)
(7.5)
называется плотностью вероятности. Она обладает следующими свойствами:
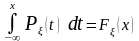 (7.6)
(7.6)
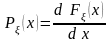 (7.7)
(7.7)
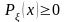 (7.8)
(7.8)
Для непрерывной
случайной величины
и числа
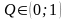 квантиль порядка Q
определяется, как число
квантиль порядка Q
определяется, как число
 ,
удовлетворяющее уравнению
,
удовлетворяющее уравнению
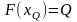 (7.9)
(7.9)
Для дискретной случайной величины , принимающей значения с вероятностями Р1, Р2, ... математическое ожидание , определяется равенством
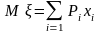 (7.10)
(7.10)
Для непрерывной случайной величины , с плотностью распределения математическое ожидание определяется равенством
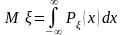 (7.11)
(7.11)
Дисперсия случайной величины определяется равенством
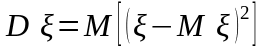 (7.12)
(7.12)
справедливо также равенство
 ,
(7.13)
,
(7.13)
из которого следуют формулы, удобные для вычисления дисперсии дискретных и непрерывных случайных величин:
 (7.14)
(7.14)
 (7.15)
(7.15)
Стандартное (или среднее квадратичное) отклонение случайной величины определяется равенством
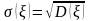 (7.16)
(7.16)
