3 Теоремы сложения и умножения. Независимость событий. Вероятность наступления хотя бы одного события из нескольких независимых

Пусть А и В два события. Тогда

Р (А +В) = Р(А) +Р(В) - Р(АВ) (3.1) Для несовместных событий Р(А+В)=Р(А)+Р(В). В случае трех событий А,В, С

Р(А +В+С) =Р(А) +Р(В) +Р(С) – Р(АВ) – Р(ВС) – Р(СА) + Р(АВС) (3.2)

Для попарно несовместных событий А,В,С Р(А+В+С)=Р(А)+ Р(В)+ Р(С).

Для двух событий А и В (Р(В)>0) вероятность наступления события А при условии, что произошло событие В, определяется равенством

(3.3)

Для событий справедливо соотношение, называемое формулой умножения событий:

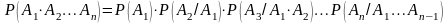(3.4)

Два события А и В называются независимыми, если выполняется равенство

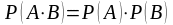(3.5)

События называются попарно независимыми, если для любых двух событий А_i и А_j выполняется равенство

(3.6)

т.е. А_i и А_j независимы (ij).

События взаимонезависимы, или независимы в совокупности, если для любых целых k и 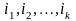таких, что , справедливо равенство

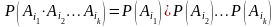(3.7)

ЗАДАЧИ

1. Монету подбросили три раза. Событие А - первый раз выпал герб. Событие В - число выпавших гербов больше числа выпавших цифр. Найти вероятность этих событий и проверить независимы ли они.

2. В группе 20 студентов, из них 15 человек получают стипендию. На дежурство по жребию отобрали двух студентов. Событие А - оба получают стипендию, В - первый из отобранных получает стипендию. Определить, зависимы ли события А и В и найти их вероятности.

3. В урне 10 белых и 5 черных шаров. Вытаскивают 3 шара случайно и без возвращения. Какова вероятность того, что они все одного цвета ? Какова вероятность того, что первый шар белый ? Зависимы ли события ?

4. События А и В несовместны, Р(А)0, Р(В)0. Зависимы ли данные события ?

5. Студент знает 10 из 30 вопросов программы. Используя теорему умножения вероятностей, определить вероятность того; что из трех предложенных ему экзаменатором вопросов студент знает а) все три вопроса; б) хотя бы один вопрос.

6. На одиннадцати карточках написано слово «производная». По одной выбирают четыре карточки. Какова вероятность того, что в порядке выхода можно прочитать слово «овод» ?

7. В коробке 9 новых теннисных мячей. Для игры берут три новых мяча. После игры их возвращают обратно. При выборе мячей новые от бывших в игре не отличаются. Какова вероятность того, что после трех игр в коробке не останется новых мячей?

8. В новогодней лотерее 20 билетов, из которых 10 выигрышных. Студент купил два билета какова вероятность того, что оба выиграют? Хотя бы один выиграет?

9. Два пеленгатора с целью обнаружить радиостанцию осуществляют независимо одновременную разведку сигналов этой станции с различных направлений на установленной ранее частоте. Определить вероятность удачного исхода разведки одновременно с двух направлений, если вероятность определения пеленга с одного направления равна 0,6 и с другого 0,7 ?

10. Вероятность того, что в электроцепи напряжение превысит номинальное значение равна 0,9. При повышенном напряжении вероятность отказа прибора равна 0,8. Определить вероятность отказа вследствие повышения напряжения.

11. При браковке деталей обнаружено, что первый дефект присутствует в среднем в двух деталях из каждых 25. В случае его отсутствия, второй присутствует в трех деталях из каждых 50. Какова вероятность взять бракованную деталь?

12. Вероятность занятости первой линии связи 0,3 , второй - 0,6 , третьей - 0,2. Какова вероятность того, что все три линии свободны?

13. На заводе три цеха. Вероятность того, что первый цех выполнит месячный план - 0,9 , второй - 0,8 , третий - 0,95. Завод выполнит план, если план выполнят хотя бы два цеха. Какова вероятность того, что завод выполнит план?

14. Два стрелка стреляют по мишеням по одному разу. Вероятность того, что попадет первый стрелок - 0,9 , второй - 0,6. Второй стрелок получает приз, если его результат не хуже, чем у первого. Какова вероятность того, что он получит приз ?

15. В цехе имеются два станка, вероятность занятости каждого из них равна 0,7. Какова вероятность, что один занят, а другой нет?

16. В блоке, содержащем 24 лампы, отказала одна лампа. Неисправность отыскивается путем поочередной проверки. Найти вероятность того, что неисправность будет устранена не более, чем при первых трех попытках.

17. Электрическая цепь между точками А и В составлена по схеме, изображенной на рисунке. Различные элементы цепи выходят из строя независимо один от другого. Вероятности выхода элементов из строя за время Т следующие:

Элемент K₁ K₂ Л₁ Л₂

Вероятность 0,1 0,2 0,4 0,5

Определить вероятность прерывания питания за указанный промежуток времени.

Рисунок 3

18. Доказать, что если Р(А) + Р(В) > 1, то А и В совместны.

19. Доказать, что если Р(А/В)>Р(А), то и Р(В/А) > Р(В).

20. Доказать, что если А и В независимы, то и , В, и , 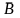независимы.

21. Доказать, что если Р(А+В)=1–Р( ) Р( ), то события А и В независимы.

22. В коробке 6 ламп, из которых 4 бракованных. Некто наугад берет лампочку, ввинчивает в патрон и включает ток. Если лампа горит, то испытания прекращаются. Если лампа не горит, то она выбрасывается и испытывается следующая и т.д. Какова вероятность того, что будет проведено не более трех испытаний ?

23. В партии из 10 изделий содержится 5 бракованных. Для проверки контролер берет наугад одно изделие из партии и проверяет его качество. Если изделие оказывается бракованным, дальнейшие испытания прекращаются, а партия задерживается. Если изделие окажется стандартным, то контролер берет следующее изделие и т.д. Какова вероятность того, что будет проверено не более трех изделий.

24. Двое игроков бросают монету два раза каждый. Какова вероятность того, что у обоих игроков выпадет одинаковое число гербов ?

25. Производится стрельба по некоторой цели, вероятность попадания в которую при каждом выстреле равна 0,6 . Стрельба прекращается при первом попадании в цель. Найти вероятность того, что будет произведено не более четырех выстрелов.

26. Вероятность того, что разговор можно вести по каждому из трех каналов связи, соответственно равна 0,8 ; 0,7 ; 0,8 . Какова вероятность того, что разговор состоится ?

27. В комплекте имеется 12 телефонных аппаратов, среди которых 3 бракованных. Какова вероятность, что среди двух взятых аппаратов хотя бы один небракованный?

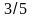28. Вероятность соединения при телефонном вызове . Какова вероятность, что соединение произойдет только при третьем вызове?

29. Вероятность появления поломок на каждой из трех соединительных линий равна 0,2 . Какова вероятность, что хотя бы одна линия исправна ?

30. На предприятии три телефона. Вероятности занятости их соответственно равны 0,6 ; 0,4 ; 0,5 . Какова вероятность, что хотя бы один из них свободен ?

31. Два пеленгатора независимо друг от друга пеленгуют объект. Первый имеет вероятность успеха 0,3 , второй - 0,4 . Какова вероятность, что объект будет запеленгован ?

32. По радиолинии передается сигнал в виде последовательности пяти импульсов. Вероятность искажения каждого импульса равна 0,1. Искажения отдельных импульсов независимы. Найти вероятность того, что передаваемый сигнал будет искажен.

33. Вероятность попадания в мишень каждым из двух стрелков равна 0,3. Стрелки стреляют по очереди, причем каждый делает по два выстрела. Попавший в мишень первым получает приз. Найти вероятность того, что приз будет получен.

34. Вероятность хотя бы одного попадания в цель при трех выстрелах равна 0,936. Найти вероятность попадания в цель при одном выстреле.