12 Предельный режим для марковских процессов

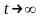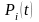Рассмотрим некоторую систему  с состояниями t=0,1,2,..., описываемую марковским процессом. Неформально предельным или установившимся режимом для системы  называется случайный процесс, устанавливающийся в системе при . Если у системы есть состояния без выхода, то при система оказывается в одном из них; если же у системы нет состояний без выхода и общее состояний конечно, то для вероятности (нахождения в состоянии i в момент t ) существует предел:

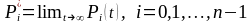, (12.1) где n – число состояний системы. Вероятности 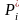называются предельными или стационарными. Для того, чтобы найти эти вероятности, в системе уравнений для вероятностей состояний (см. 12.3) приравнивают нулю части уравнений, т.е. производные . Затем решают полученную систему алгебраических уравнений вместе с уравнением нормировки 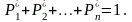Пример составления и решения уравнений приведен в решении задачи 3.1.

Рассмотрим марковский процесс, описывающий систему с графом состояний следующего вида:

Рисунок 11

Здесь число состояний может быть как конечным, так и счетным. Эти процессы получили название «процессов гибели и размножения». В случае конечного числа стационарные, или предельные вероятности существуют при любых значениях параметров 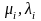. В случае счетного числа состояний для существования этих вероятностей необходимо и достаточно выполнение следующего условия: ряд

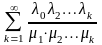сходится.

Предельные вероятности 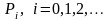( в случае, когда они существуют) могут быть найдены по формулам

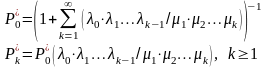(12.2)

ЗАДАЧИ

1. Поселковая телефонная станция (ТС) соединена одной телефонной линией с райцентром. Если на ТС поступает требование на разговор с райцентром и линия свободна, то происходит соединение запрашивающего абонента с ТС райцентра. Кроме простых требований бывают срочные вызовы районных спецслужб (01, 02, 03). Если поступает срочный вызов, а линия занята обычным разговор, то этом разговор прерывается и линия отдается срочному вызову. Известно, что поток обычных и срочных разговоров простейшие с параметрами ₁ и ₂. Длительность обычных разговоров подчиняется показательному распределению с параметром ₁, продолжительность срочных разговоров - показательному распределению с параметром ₂. Надо найти долю времени, затрачиваемого на передачу по линии разговоров обычных и срочных.

Решение. Введем три состояния:

0,1,2 - линия связи свободна, линия занята «обычным» разговором и занята срочным разговором. Нарисуем граф переходов

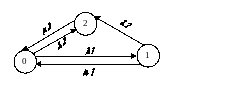
Рисунок 12

Составим системы дифференциальных уравнений для вероятностей 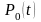, , 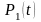(см. формулы 10.7).

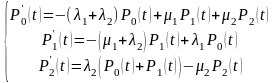(12.3)

Т.к. у графа на рисунке 12 конечное число состояний, то должны существовать предельные вероятности . Для их отыскания из системы (12.3) получаем систему алгебраических уравнений, приравнивая к нулю значения производных и добавляя условие нормировки:

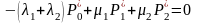
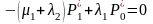
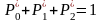
Решая эту систему уравнений, легко находим:

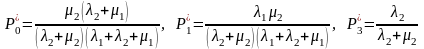
Таким образом, получаем, что доля времени когда линия занята срочным разговором, равна 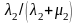«простым» разговором – .

2. Для предыдущей задачи найдите вероятность того, что линия занята, при условии, что срочные разговоры отсутствуют.

3. Для систем, приведенных на рисунке 13 надо найти предельные вероятности .

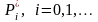4. Рассматривается работа вычислительной машины. Поток отказов (или поломок) машины простейший с показателем . Время устранения поломки подчиняется показательному распределению с параметром . Считая, что машина находится в стационарном режиме, определить долю времени, затрачиваемого на её ремонт.

5. Некоторое устройство в процессе эксплуатации может выходить из строя, что приводит к остановке производственного конвейера. Для того, чтобы уменьшить простой, имеется еще одно, запасное устройство, идентичное первому. Если 1-е устройство ломается, то его заменяют на резервное и начинают ремонтировать. Время ремонта – случайная величина, подчиняющаяся экспоненциальному распределению с параметром . Поток поломок можно считать простейшим с параметром . Считая, что процесс находится в стационарном режиме, определить долю времени простоя конвейера, вызванного поломкой обоих блоков. (В этом случае сначала ремонтируют одно устройство и его устанавливают, затем сразу начинают ремонт второго).

6. В условиях задачи 5 для уменьшения простоев добавили еще одно устройство. Определить долю времени простоев в этом случае.

а) б)

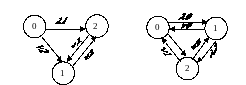
в) г)

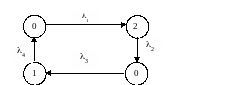
д)

Рисунок 13

7. Рабочий ремонтирует два одинаковых станка-автомата. Поток поломок каждого станка можно считать простейшим с параметром , время ремонта - случайная величина, подчиняющаяся экспоненциальному распределению с параметром . Считая, что процесс находится в стационарном режиме, определить долю времени, когда работают оба станка (Р₀), один станок (P₁) и ни одного (Р₂).

8. В часовой мастерской работают мастер и ученик. Если приходит клиент и мастер свободен, то он обслуживает клиента, а если же мастер занят, то клиент поступает к ученику. В случае, когда клиент приходит, а мастер и ученик заняты, клиент уходит. Поток клиентов простейший с параметром . Время обслуживания клиентов и мастером и учеником -случайная величина, подчиняющаяся показательному распределению с параметрами ₁ и ₂, соответственно. Считая режим работы мастерской стационарным, найти долю времени, когда мастер (Р_м) и ученик (Р_у) работают.

Указание. Введите 4 состояния системы: 0.0- мастер и ученик свободны, 1.0 - мастер занят, ученик свободен, 0.1 - мастер свободен, ученик занят, 1.1 – оба заняты. Тогда Р_м = Р_1.0 +Р_1.1, Р_у = Р_0.1+ Р_1.1 .

9. В институте два лифта, расположенных рядом. Студент, подходящий к лифту, либо вызывает свободный лифт, либо, если оба лифта заняты, идет пешком. Считая, что поток студентов простейший с интенсивностью , а время, на которое занимает лифт студент случайная величина, подчиняющаяся экспоненциальному распределению с параметром , определить долю времени, когда оба лифта свободны, считая, что режим работы лифтов установившийся, т.е. стационарный.

10. (Задача-шутка). Каждый студент второго курса СибГУТИ в течение семестра выполняет ряд заданий (домашние и расчетные работы, курсовые работы, подготовка к коллоквиумам и т.п.). Поток заданий можно приближенно считать простейшим с показателем =0,2 (штук в день), а время, затрачиваемое на выполнение задания, можно считать случайной величиной, подчиняющейся экспоненциальному распределению. Студент А затрачивает на выполнение одного задания, в среднем, один день, а студент В - три дня. Через обозначим вероятность того, что студент в момент t должен выполнить п накопившихся заданий (n= 0,1,2,...). Определить: 1) существует ли для вероятностей предельные значения для студентов А и В; 2) объяснить качественно полученные результаты; 3) найти предельную вероятность Р₀ для того случая, когда она существует.

Указание. Использовать формулу для суммы геометрической прогрессии.

11. В условиях задачи 10 определить, с какой скоростью надо выполнять задания студенту для того, чтобы 90% внеучебного времени было свободно от выполнения заданий.

Указание. Скорость выполнения заданий совпадает со значением параметра  показательного распределения.

12. В комнате учреждения работают три сотрудника, каждый из них пользуется телефоном в среднем 1 раз в час, а средняя продолжительность одного разговора - 6 минут. Считая, что время разговора - случайная величина, подчиняющаяся экспоненциальному распределению, а поток звонков - простейший - определить долю времени, в течение которого занят телефон.