§ 5. Поняття про подвійний інтеграл. Зведення подвійного інтегралу до повторного

5.1. Поняття про подвійний інтеграл

При введені поняття визначеного інтеграла ми розв’язували задачу про

знаходження площі криволінійної трапеції. Проте, часто необхідно знайти об’єм деякої просторової фігури. Розв'яжемо задачу: знайти об’єм тіла обмеженого

зверху неперервною поверхнею ( ), знизу скінченою замкненою областю S площини xOy, з боків прямою циліндричною поверхнею побудованою на межі області S, перпендикулярно до площини xOy.

Знайдемо об’єм V тіла зображеного на малюнку 14. Розіб’ємо область S деякими лініями на n частин з площами відповідно S₁, S₂... S_n.В кожній з частин виберемо по одній точці P₁(x₁,y₁), P₂(x₂,y₂)…P_n(x_n,y_n) і побудуємо циліндри з основами S_i і висотами P_iQ_i=f(x_i,y_i). Тоді об’єм V

. (6.51)

Ця сума називається двомірною інтегральною сумою для функції по

області S. Для цієї суми виконується теорема існування подвійного інтеграла:

Якщо функція, неперервна в обмеженій замкнутій області S і якщо число частинок n, на які розбита область S, необмежено зростає, а найбільша відстань між двома точками кожної частинки, які лежать на границі ( ) , прямує до 0, то існує границя двомірної інтегральної суми (6.50), величина якої не залежить ні від способу розбиття S ні від вибору точки P_i всередині частинки з площею S_i.

Ця границя називається подвійним інтегралом від функції поширеним на область S і позначається . Тобто

.

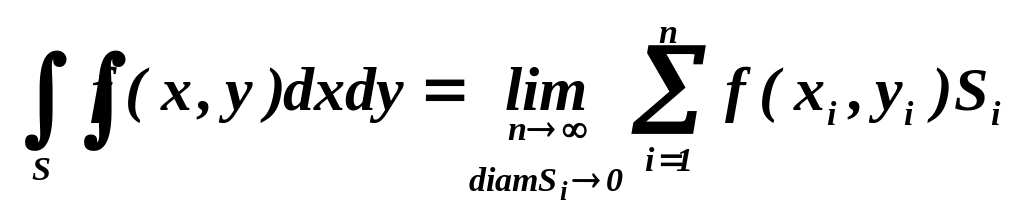Треба зазначити, що якщо , то автоматично . Тому можна записати (6.52)

5.2. Повторний інтеграл. Перехід від подвійного інтеграла

до повторного

Підійдемо до задачі про знаходження об’єму V поверхні по іншому. Врахуємо, що область S в площині xOy обмежена зверху і знизу певними лініями і .Разом з тим, функції і неперервні на [аb]. Проведемо переріз нашого тіла площиною х= х_і, паралельно до координатної

площини zOy так, що a<x<b. (мал..15) Площа перерізув изначається як деяка функція від х , тобто S=F(x).

В такому випадку об’єм тіла

. (6.53)

Визначимо тепер функцію F(x). Так 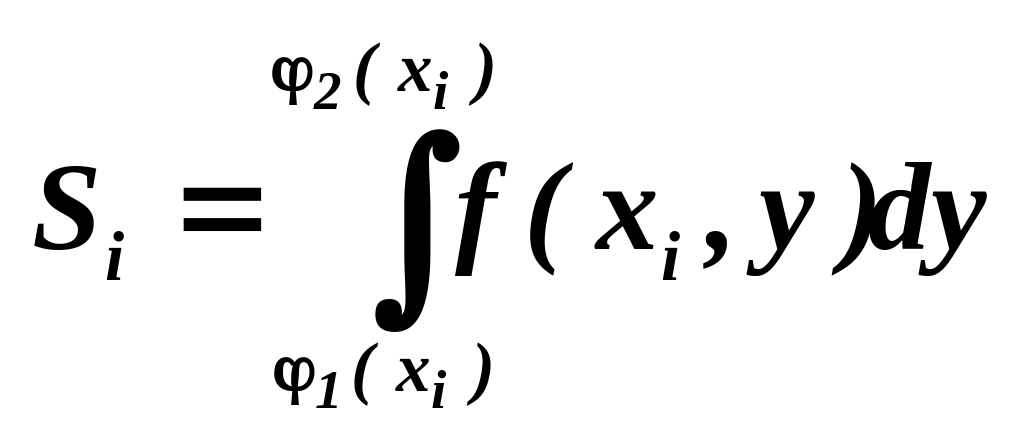. А це значить, що

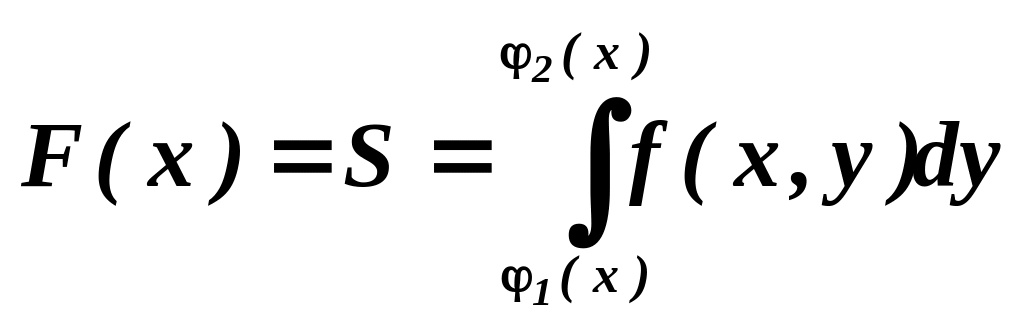(6.54)

Об'єднавши формули (6.53) і (6.54) одержуємо

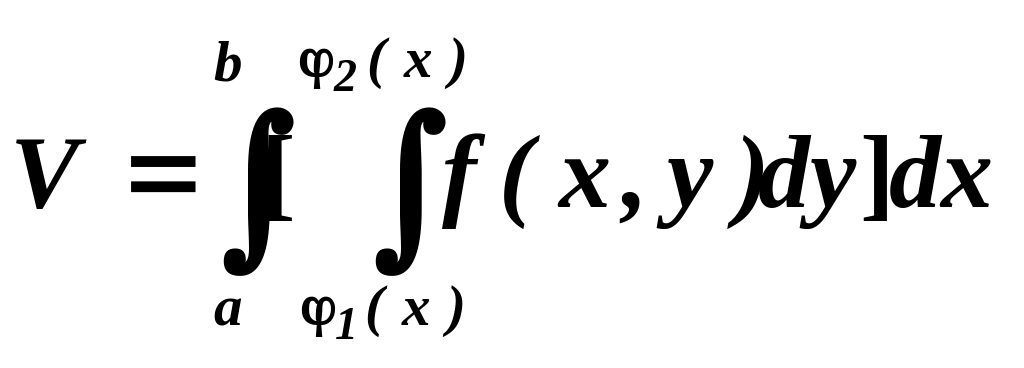. (6.55)

Інтеграл (6.55) називається повторним інтегралом, поширеним на довільну область S. Зауважимо, що якщо б область була обмежена кривими і ( неперервними на (c,d)) то отримали б, що 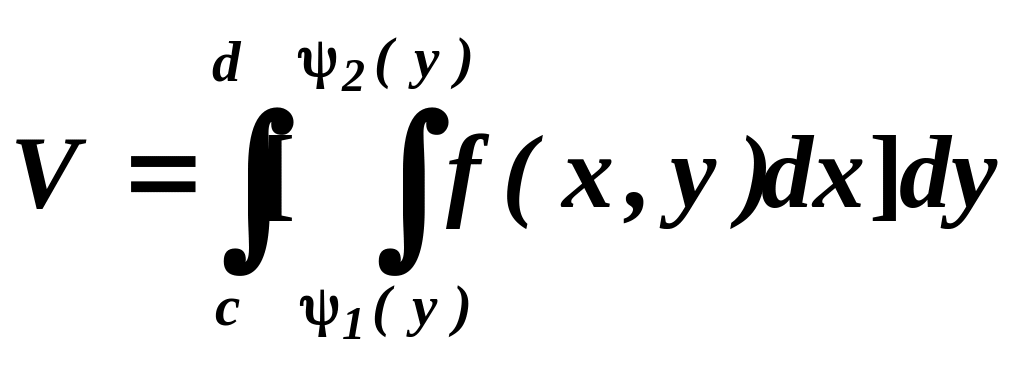, також повторний інтеграл.

Отже, обчислення подвійного інтеграла можна звести до обчислення повторного.

5.3. Інтеграл Ейлера-Пуассона

В теорії ймовірності і математичній статистиці велику роль відіграє інтеграл Ейлера-Пуассона: (6.56)

Він належить до інтегралів, які не виражаються в елементарних функціях. Обчислимо його з допомогою подвійного інтеграла. Застосуємо формули зв’язку між декартовими і полярними координатами

Врахуємо те, що визначений інтеграл не залежить від позначення змінної

(інваріантність визначеного інтеграла відносно змінної).

Тому можемо записати (6.57)

Перемноживши формули (6.56) і (6.57) , одержимо

.

Врахувавши,що і ,

Одержимо:

.

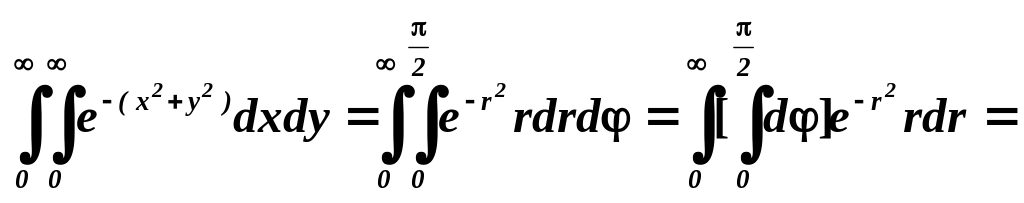
З одержаної рівності визначаємо, що . Тобто .

А тепер визначимо інтеграл Ейлера-Пуасона

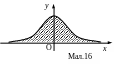
(6.58)

Геометрично, інтеграл Пуассона виражає собою площу фігури (мал.16.), обмеженої графіком функції (крива Гаусса) і віссю Ох.

354