У випадку, коли потрібно обчислити інтеграл його розбивають на суму двох і обчислюють кожен інтеграл окремо.

3.2. Інтеграл від розривної функції

Нехай визначена на і має точку розриву при .

Отже - відповідний невласний інтеграл від розривної функції. Якщо f(x) визначена на (a,b і x=a точка розриву, то . Якщо ж має точку розриву , то .

Якщо для інтегралів пунктів (6.3.1) і (6.3.2) відповідні їм границі існують, то інтеграли називаються збіжними. Якщо границі не існують або нескінченні, то інтеграли називаються розбіжними.

Приклад 26.

. Це є розбіжний інтеграл.

Приклад 27. Обчислити

Розв’язування. . Досліджуємо цю границю:

якщо р<1, ;

p>1, ;

p=1, .

Значить, даний інтеграл розбіжний при p1 і збіжний при p>1. Його часто використовують при дослідженні рядів на збіжність.

§ 4. Застосування визначених інтегралів

4.1. Обчислення площ

Площа фігури, яка обмежена графіком функції y=f(x) прямими x=a і x=b, а також віссю Ox, визначається за формулою

. Площа ж фігури, яка обмежена графіками функцій та ( ), прямими і визначається за формулою

. (6.48)

П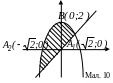 риклад 28. Знайти площу фігури, обмеженої лініями у2-х², ух. (мал. 10).

Розв’язування. а) Будуємо ескіз графіків функцій: у2-х²,

( парабола, яка перетинає вісь Ох

в точках А₁( ;0) і А₂(- ;0), вершина параболи знаходиться в точці В(0;2)), ух - пряма, бісектриса 1- го і 3-го координатних кутів.

б) Знайдемо точки перетину графіків даних функцій (межі інтегрування). Розв’яжемо рівняння: 2-х²х; -х²-х+20.

Одержуємо розв’язки: х₁= 1, х₂= -2.

в) далі, за формулою (6.46) обчислюємо площу фігури:

(кв. од.).

Приклад 29. Обчислити площу фігури, обмеженої лініями,

у=0, , .

Розв’язування. Будуємо графіки функцій (мал.11). Записуємо фор-

мулу для знаходження площі . Бачимо, що

записати одним виразом неможливо. Верхня межа даної площі, складається з двох: ( на інтервалі ) та у=0 (на інтервалі ). є нулем функції . Тому

.

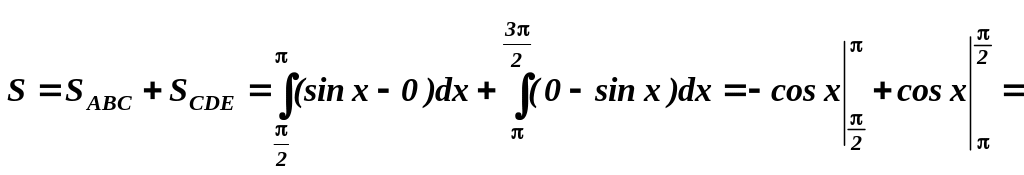
Інтеграл же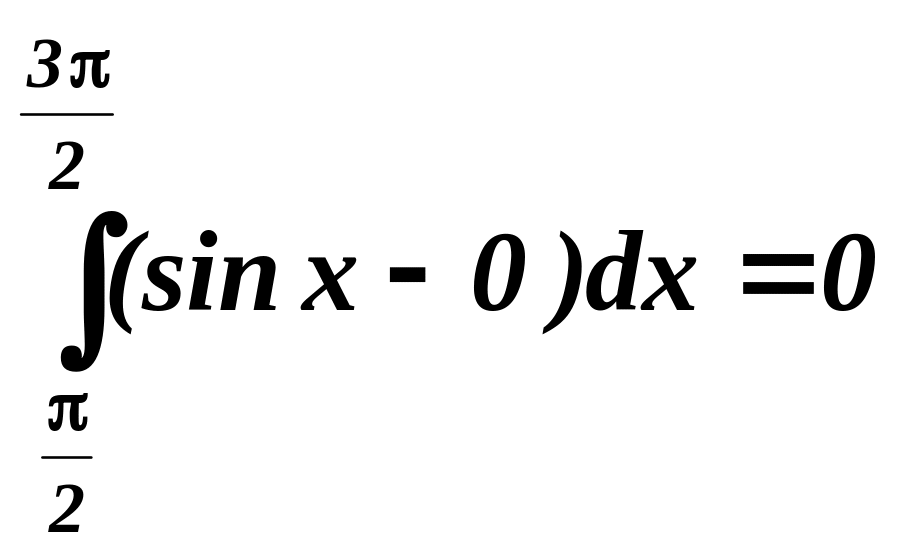 . Тому, при застосуванні визначеного інтеграла, для знаходження площ, необхідно враховувати нулі функцій, які обмежують площу (мал.3). Проміжок інтегрування, врахувавши нулі функцій, розбивають, і тоді шукана площа дорівнює сумі абсолютних величин відповідних визначених інтегралів.

4.2. Задача про розподіл доходів населення держави

Рівень розвитку держави характеризується тим, як вона забезпечує рівень життя своїх громадян. Одним з таких показників є матеріальний добробут. Легко і досить точно проводити такий порівняльний аналіз маючи певні кількісні характеристики. Доброю характеристикою для цього є коефіцієнт Джіні, який показує нерівність в розподілі доходів населення. Він безпосередньо зв’язаний з кривою Лоренца, яка відображає залежність відсотка доходів населення від відсотка тих, які ці доходи мають. Розглянемо це на прикладі.

Приклад 30. Нехай , крива Лоренца, визначена за дослідженнями розподілу доходів в якійсь країні, де х-відсоток населення, у – відсоток доходів населення. Обчислити ко-

ефіцієнт Джіні. (0<k<1).

Розв’язування. З малюнка видно, що ,

Д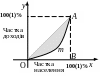 ля знаходження введемо заміну , тоді нижня межа t=0, а верхня .

Обчислюємо

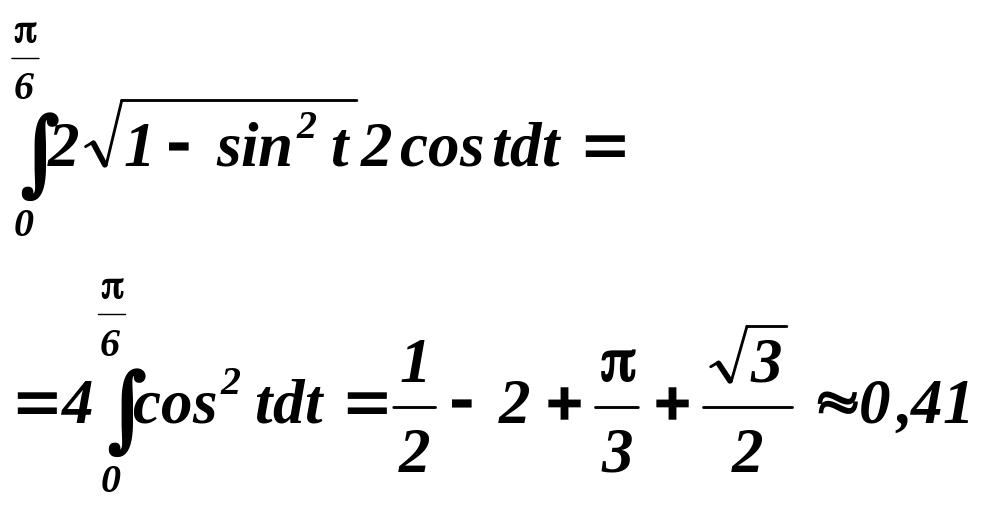
. Тому . Великий коефіцієнт k показує нерівномірність розподілу доходів серед населення даної країни.