2.1.5. Плоскость в пространстве.

2.1.5.1. Определение плоскости. Векторное уравнение плоскости. Общее уравнение плоскости. Пусть в пространстве задан ненулевой вектор N(A, B, C) и точка М₀(x₀, y₀, z₀). Плоскость задается как геометрическое место точек М (x, y, z) пространства таких, что вектор М₀М ортогонален вектору N. Таким образом, получаем векторное уравнение плоскости

.

(скалярное произведение ортогональных векторов равно нулю). Вектор N называется нормальным вектором плоскости.

В координатном виде векторное уравнение имеет вид

А(х – х₀) + В(у – у₀) + С(z – z₀) = 0

(уравнение плоскости, проходящей через точку М₀(x₀, y₀, z₀) и имеющей нормальный вектор N(A, B, C)). Преобразуем это уравнение: Ах + Ву + Сz + (–Ах₀ –Ву₀ –Сz₀) = 0, или Ах + Ву + Сz + D = 0, где D = (–Ах₀ – Ву₀ – Сz₀).

Уравнение

Ах + Ву + Сz + D = 0

называется общим уравнением плоскости. Координаты х, у, z входят в это уравнение в первой степени, поэтому плоскость называют поверхностью первого порядка.

Связкой плоскостей называют совокупность плоскостей, проходящих через одну точку. Очевидно, уравнение А(х – х₀) + В(у – у₀) + С(z – z₀) = 0 при произвольных (не равных нулю одновременно) коэффициентах А, В, С есть уравнение связки плоскостей, проходящих через точку М₀(x₀, y₀, z₀).

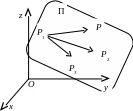
2 .1.5.2. Угол между плоскостями. Даны две плоскости П₁: А₁х + В₁у + С₁z + D₁ = 0 с нормальным вектором N₁(A₁, B₁, C₁) и П₂: А₂х + В₂у + С₂z + D₂ = 0 с нормальным вектором N₂(A₂, B₂, C₂). Очевидно, косинус угла между плоскостями равен косинусу угла между нормальными векторами, поэтому . Если требуется определить острый угол между плоскостями, то .

2.1.5.3. Условия параллельности и перпендикулярности плоскостей. Плоскости параллельны тогда и только тогда, когда коллинеарны их нормальные векторы, т.е.условие параллельности прямых имеет вид . Если выполняются равенства , то уравнения А₁х + В₁у + С₁z + D₁ = 0 и А₂х + В₂у + С₂z + D₂ = 0 определяют одну и ту же плоскость.

Плоскости перпендикулярны тогда и только тогда, когда ортогональны их нормальные векторы, т.е.условие перпендикулярности прямых имеет вид .

Т ак, уравнения 2x + 3y – 4z + 5 = 0 и –6x – 9y + 12z – 15 = 0 задают одну и ту же плоскость; уравнения 2x + 3y – 4z + 5 = 0 и –6x – 9y + 12z + 1 = 0 задают параллельные плоскости; уравнения 2x + 3y – 4z + 5 = 0 и –6x + 4y – 15 = 0 задают перпендикулярные плоскости.

2.1.5.4. Расстояние от точки до плоскости. Пусть плоскость П задана уравнением

A x + B y + C + D = 0, M₀(x₀, y_0, z₀) – произвольная точка пространства. Для любой точки М₁(x₁, y₁, z₁), лежащей на плоскости, расстояние d от точки M₀ до плоскости П равно абсолютной величине проекции вектора на нормальный вектор N(A, B, С). Пусть точка М₁ имеет координаты (x₁, y_1, z₁), тогда , и

, так как из принадлежности точки М₁ плоскости П следует, что Ax₁ + By₁ + Cz₁ + D = 0, т.е. (-Ax₁ - By₁ - Cz₁) = D.

2.1.5.5. Плоскость, проходящая через три данные точки. Даны три точки М₁(x₁, y₁, z₁), М₂(x₂, y₂, z₂), М₃(x₃, y₃, z₃), не лежащие на одной прямой (т.е. векторы и не коллинеарны). Введем в задачу точку М(x, y, z) – текущую точку плоскости. Векторы , и лежат в одной плоскости, т.е. компланарны, следовательно, их смешанное произведение равно нулю: , или, в координатной форме, .

2.1.5.6. Уравнение плоскости в отрезках – это уравнение вида . Параметры а, b и с равны, соответственно, абсциссе, ординате и аппликате концов отрезков, отсекаемых прямой на осях Ох, Оу и Oz. Общее уравнение Ах + Ву + Сz + D = 0 приводится к уравнению в отрезках при : .