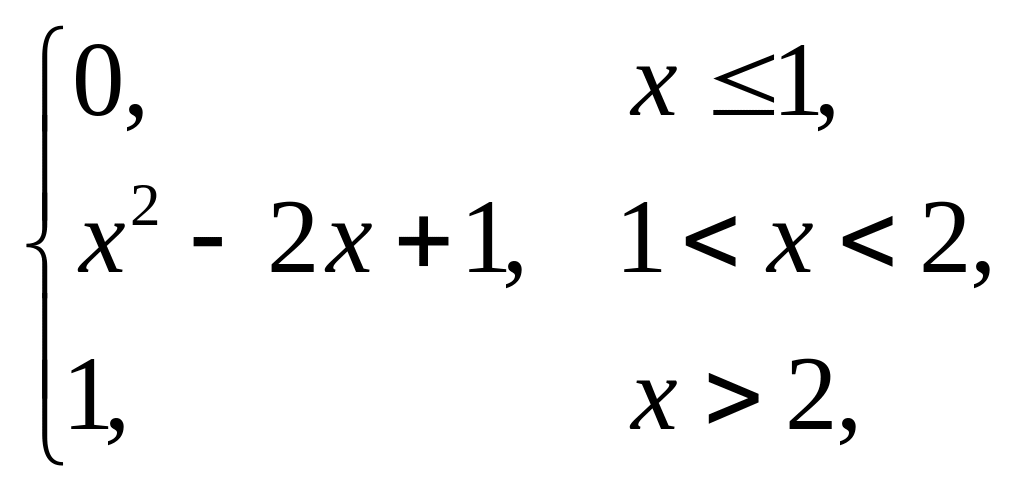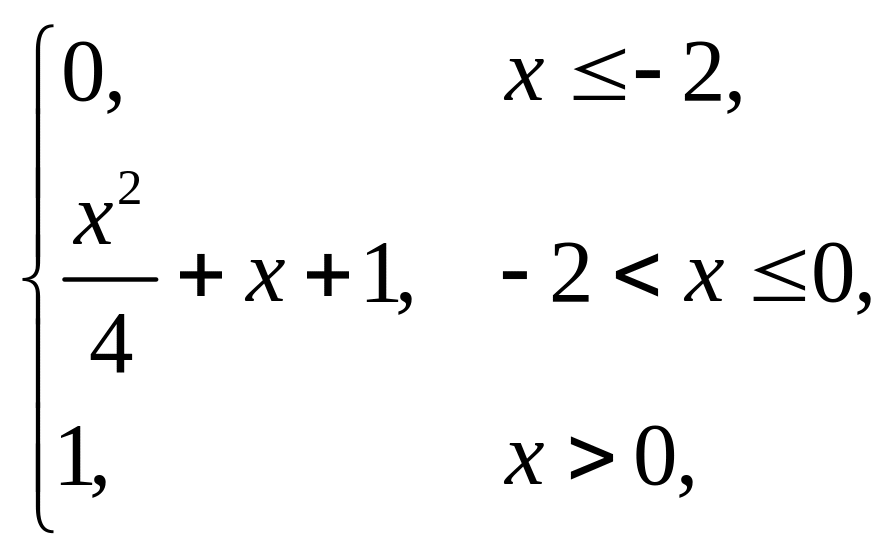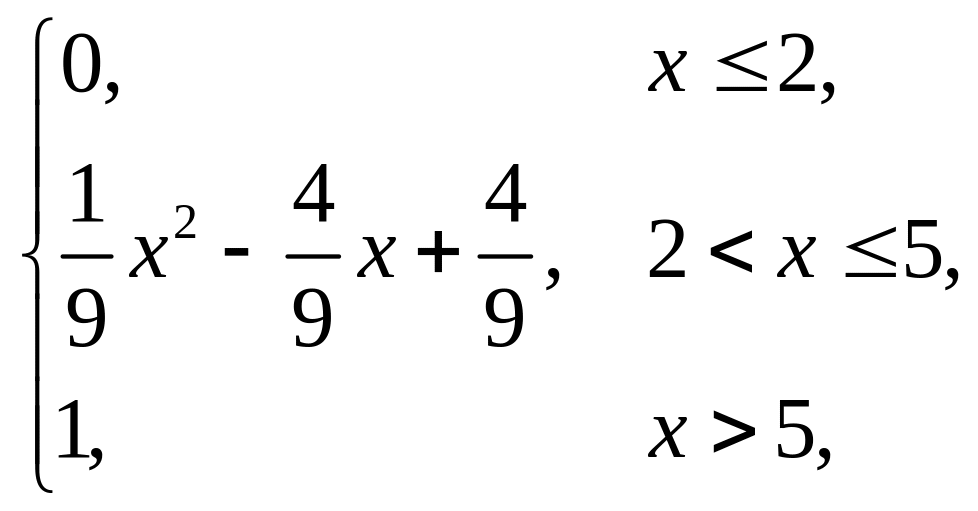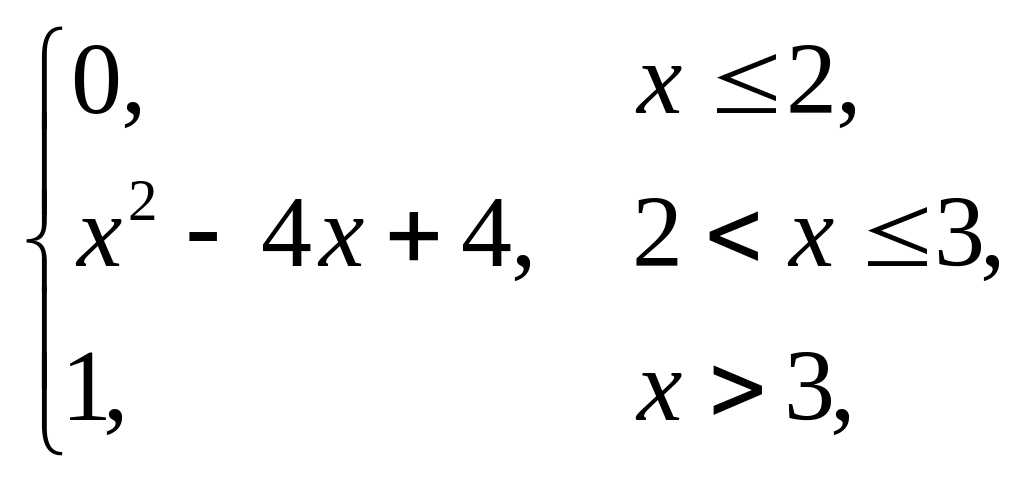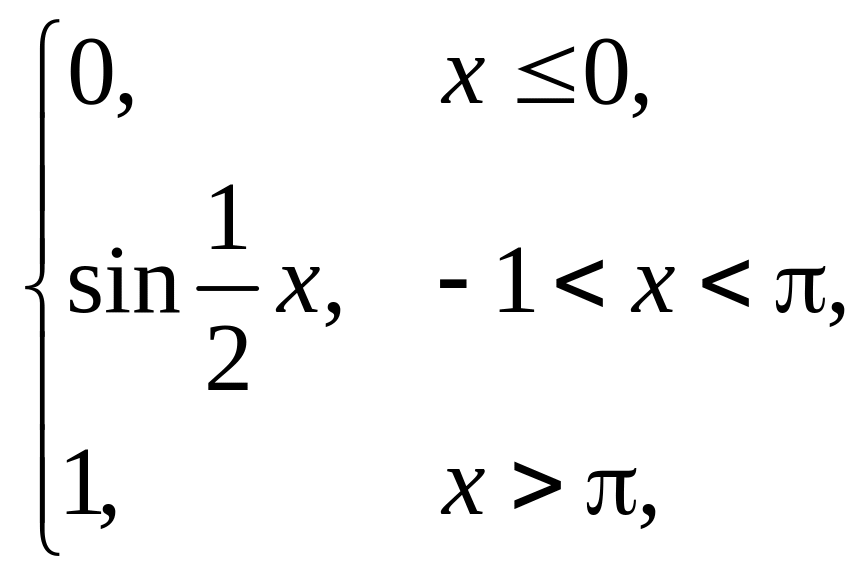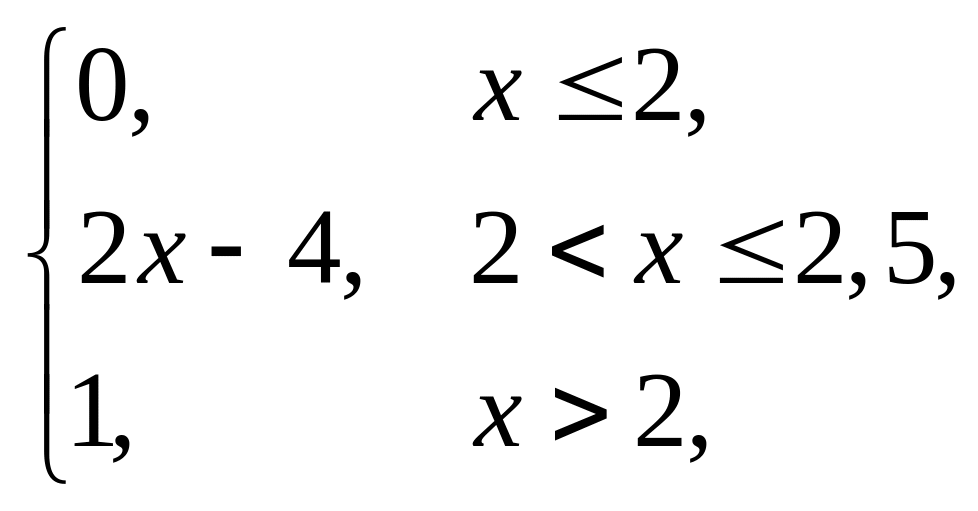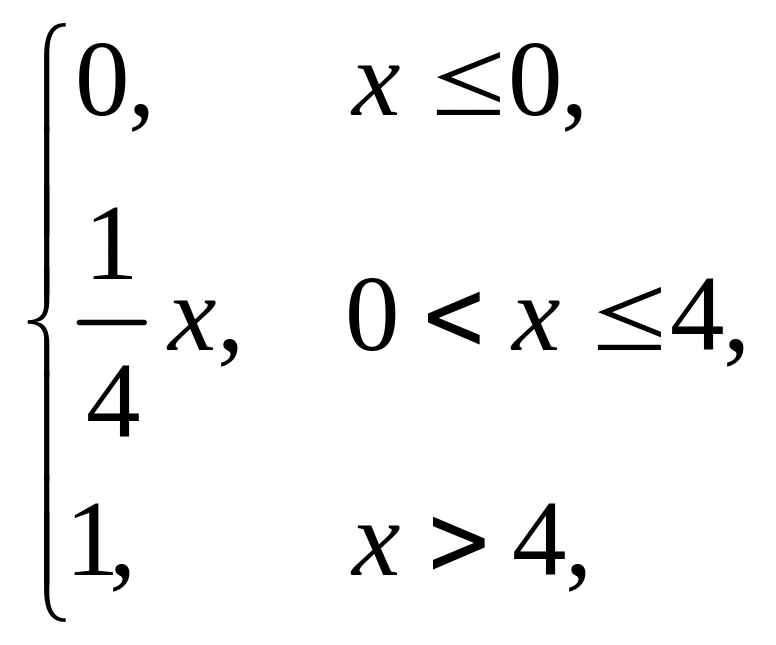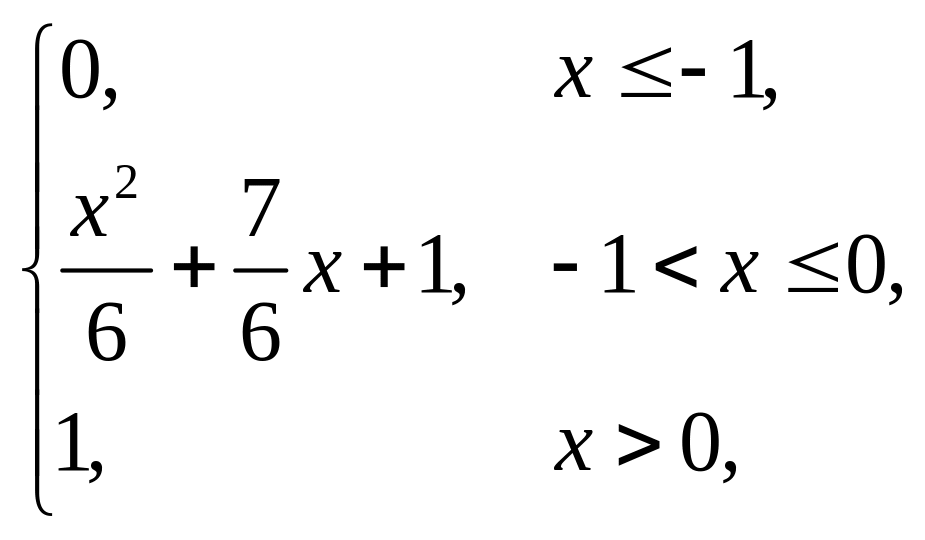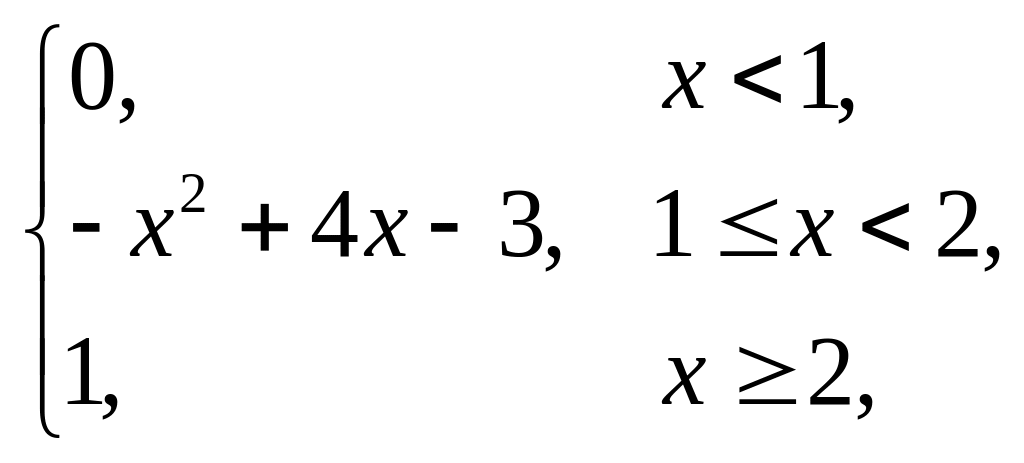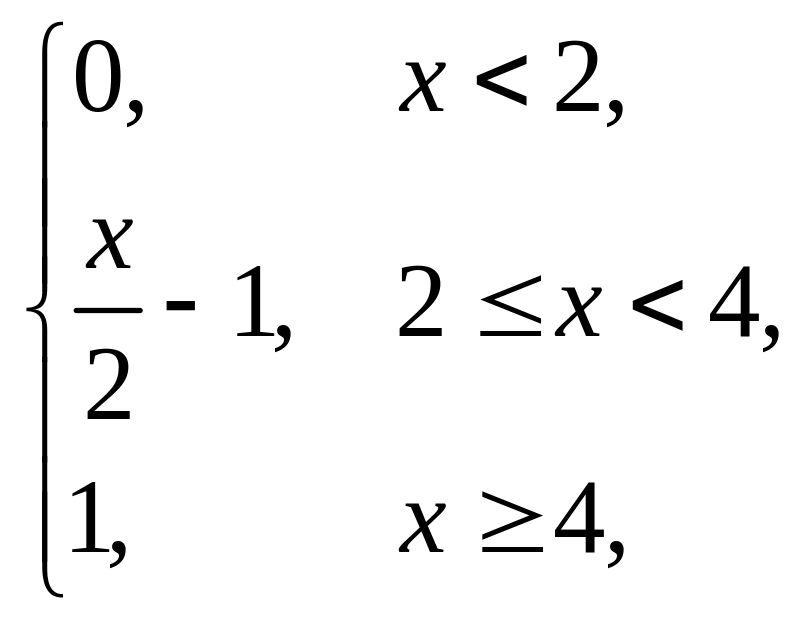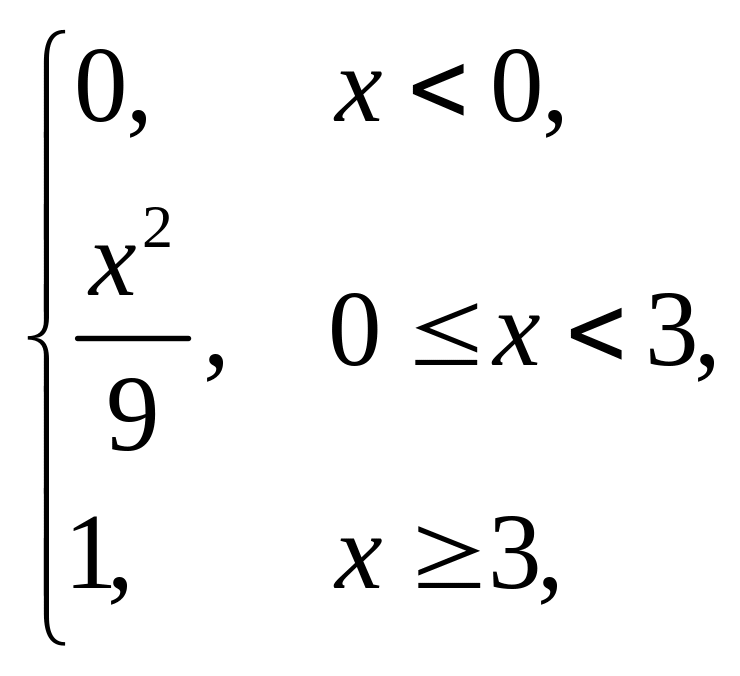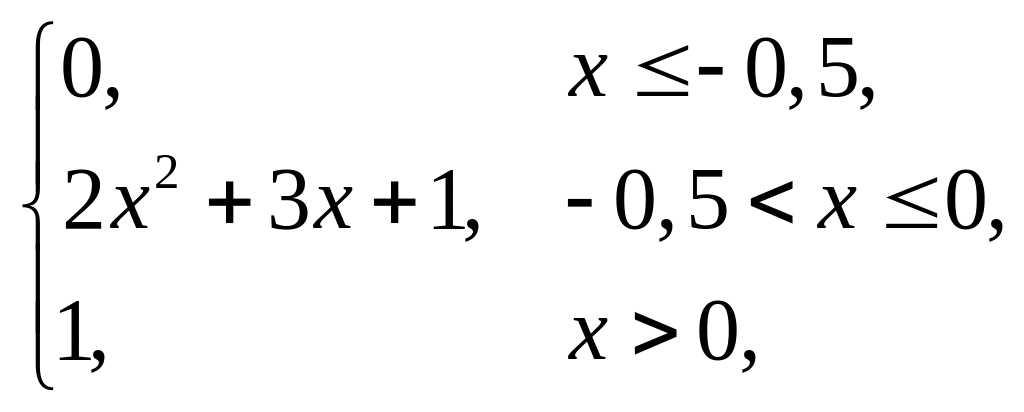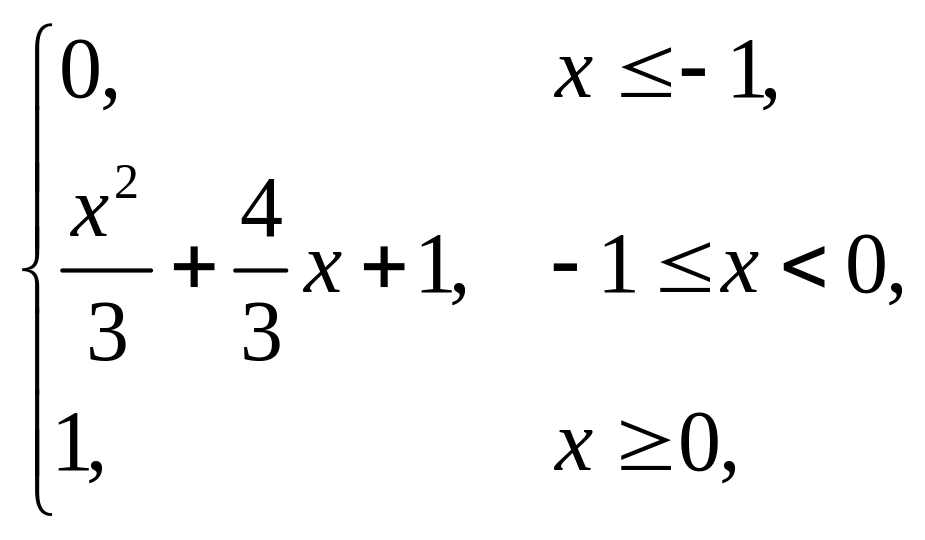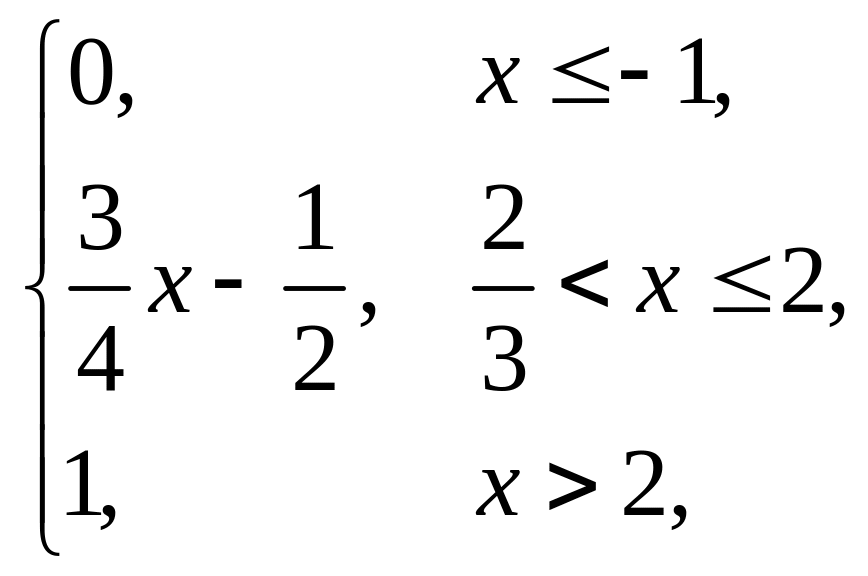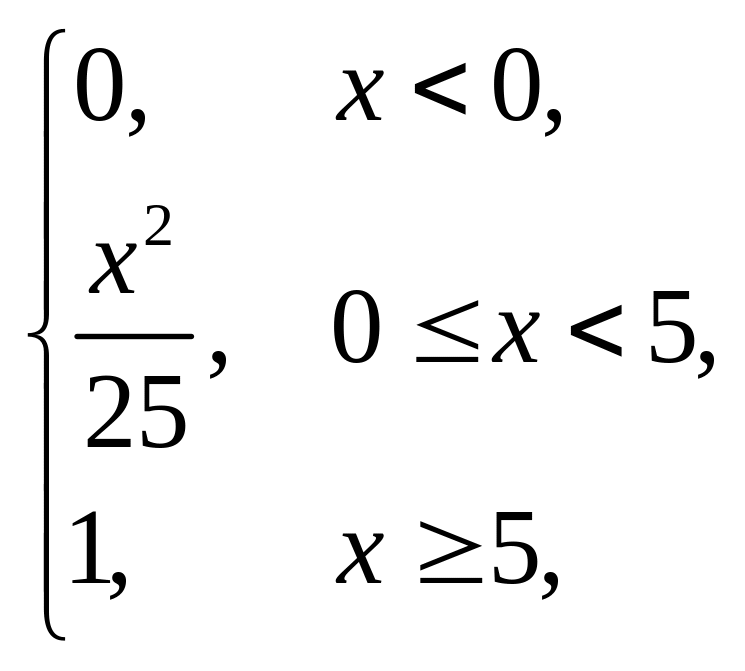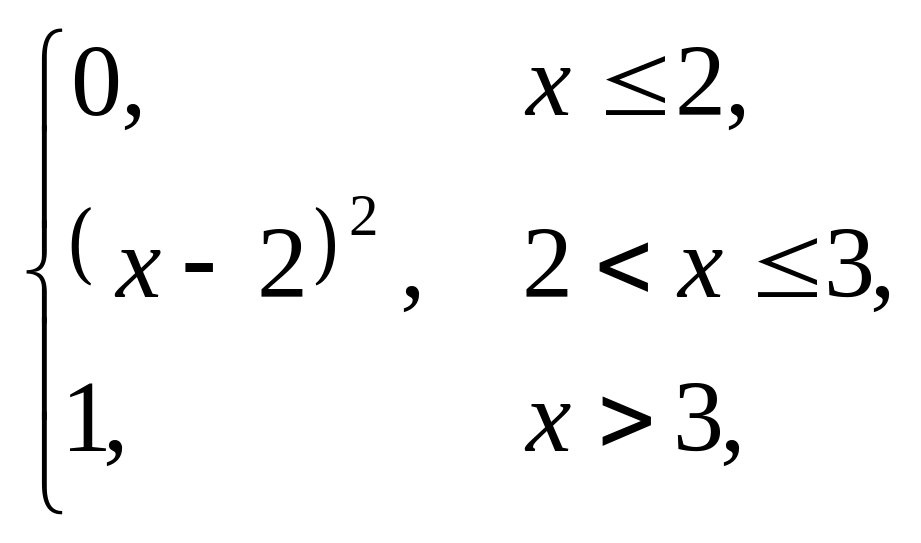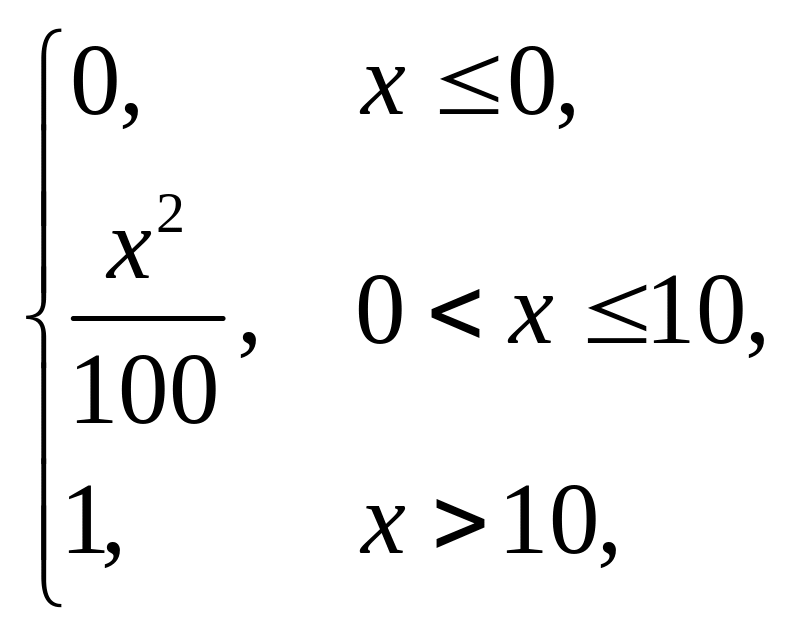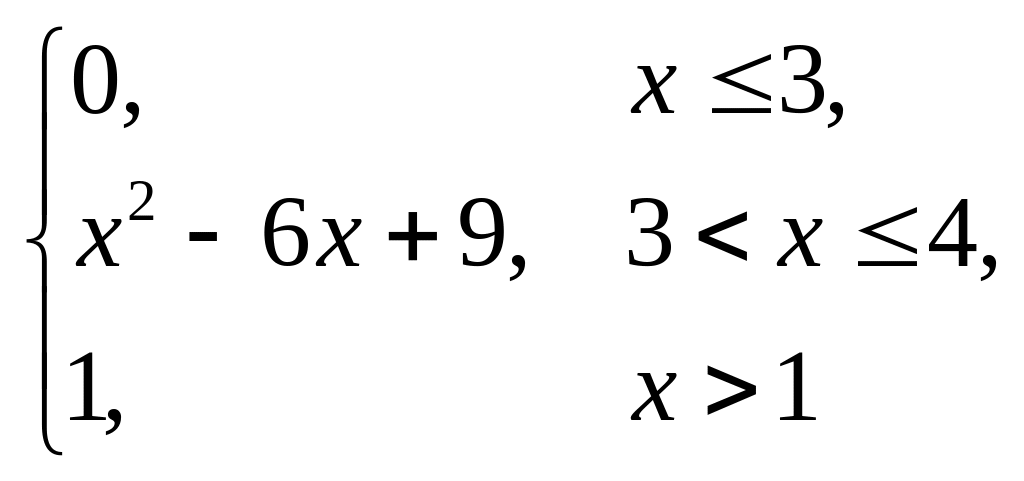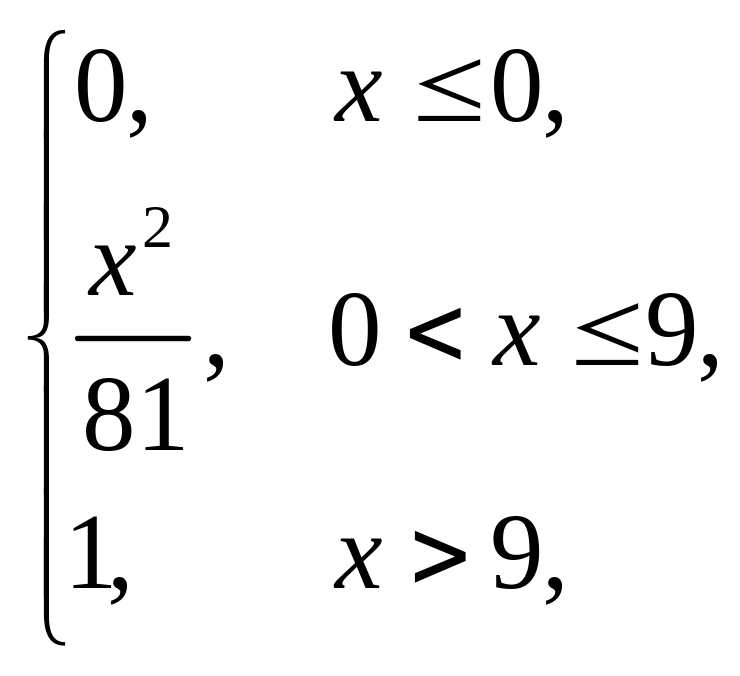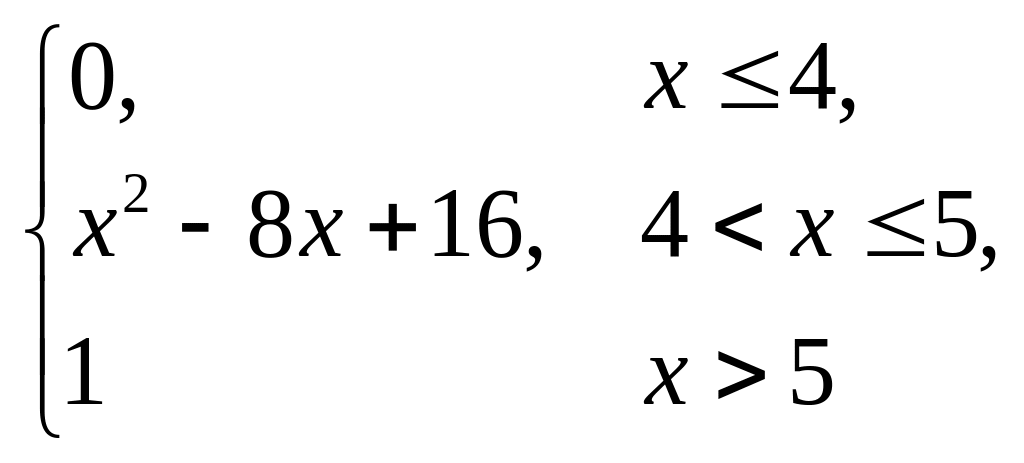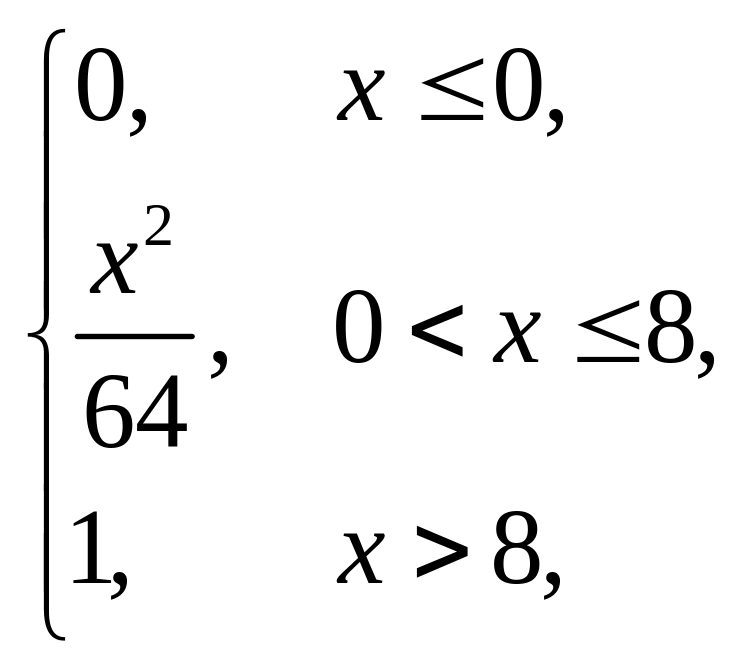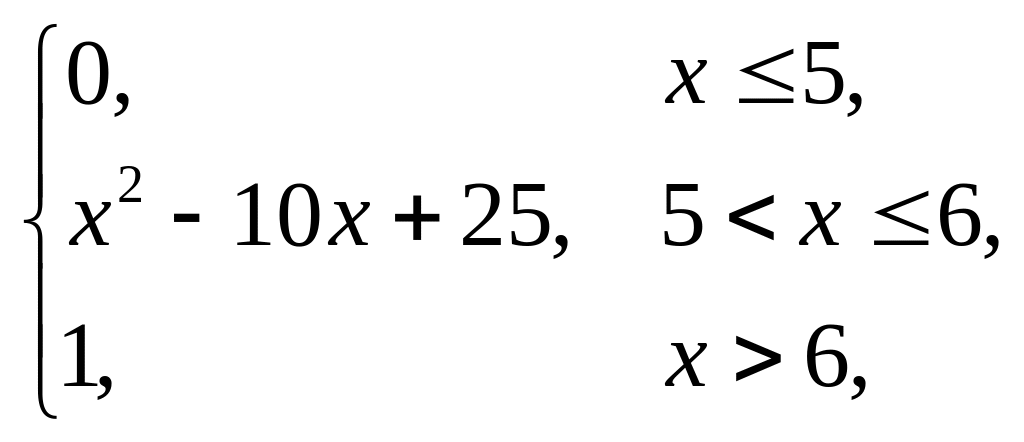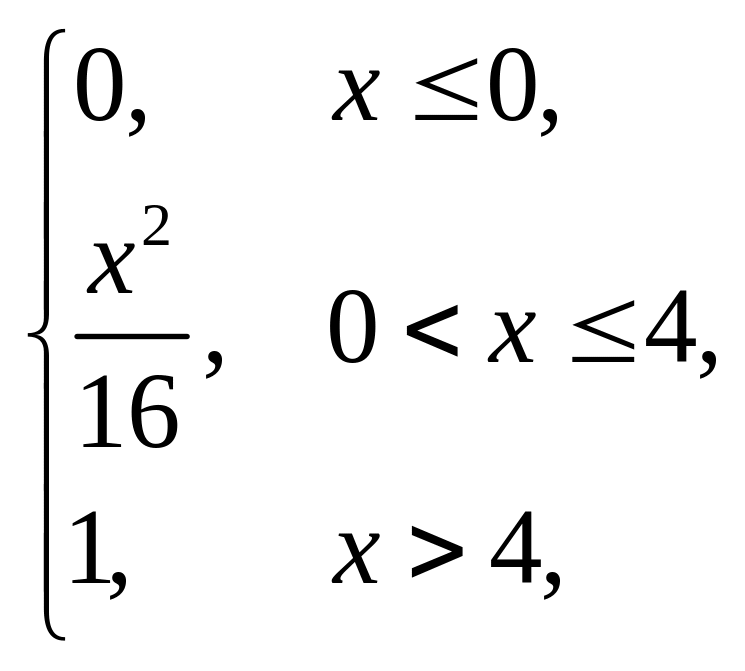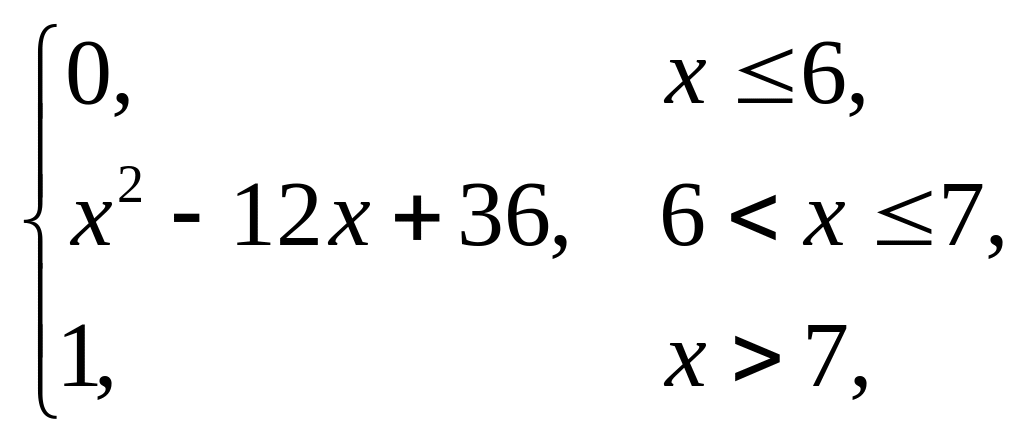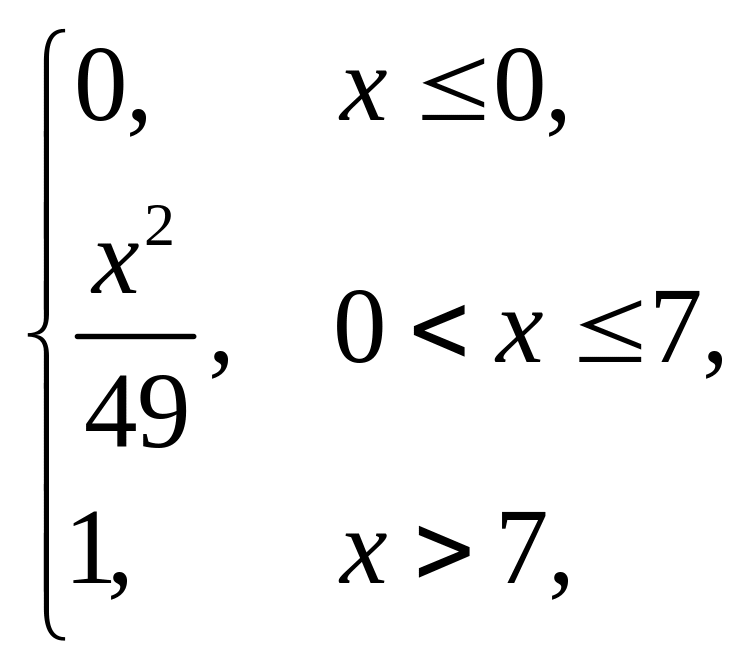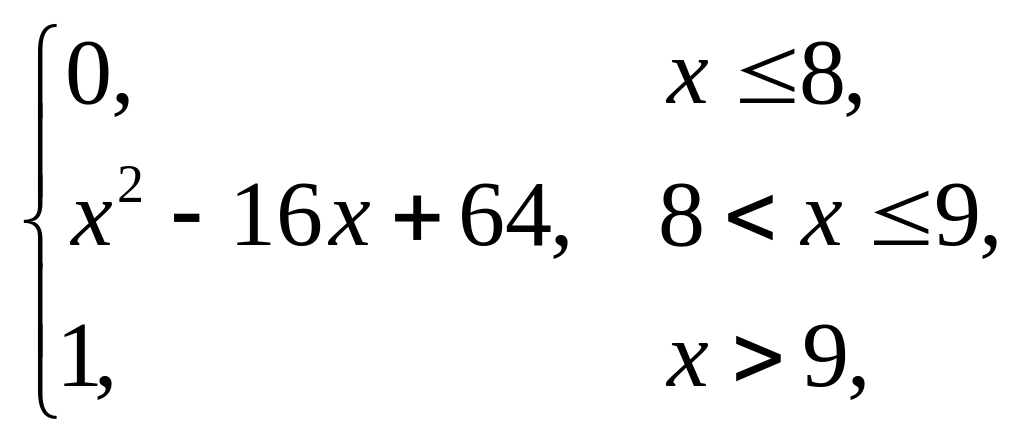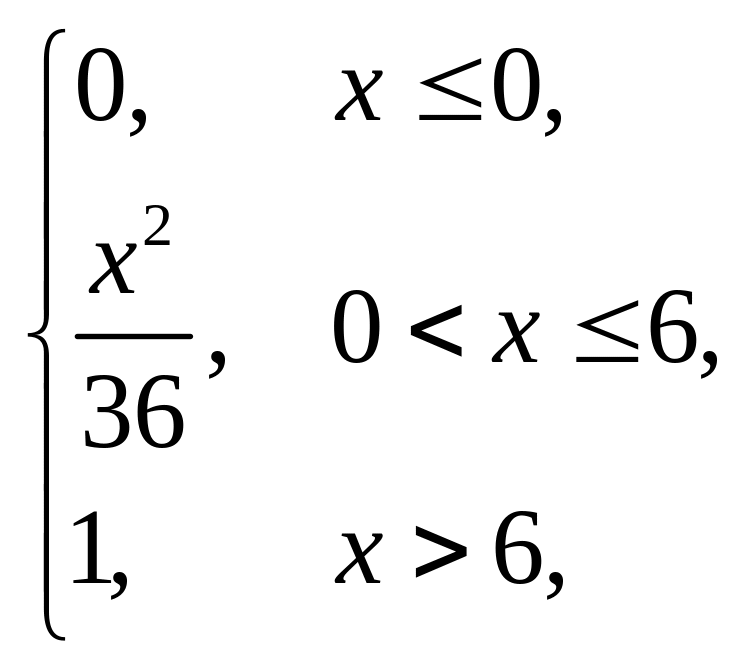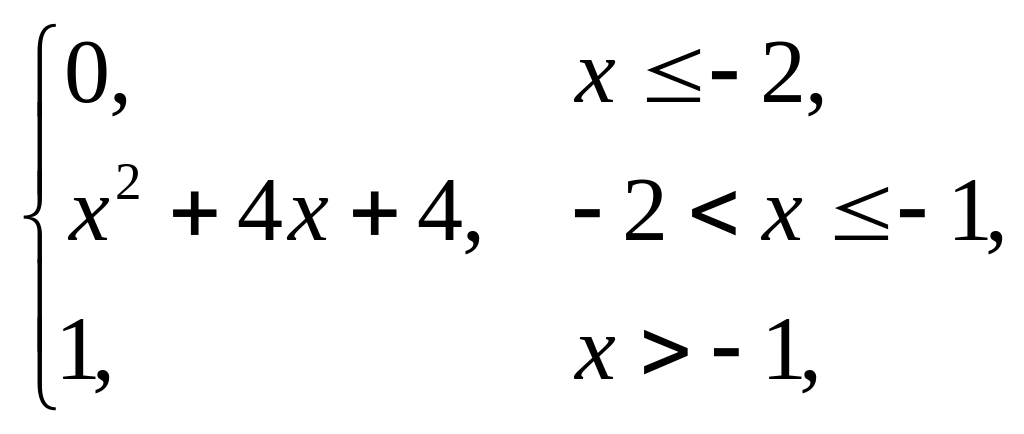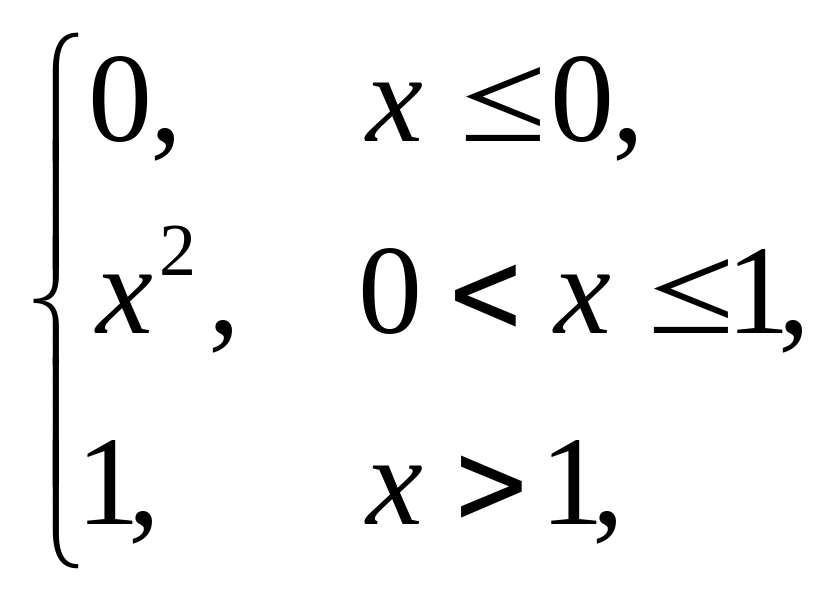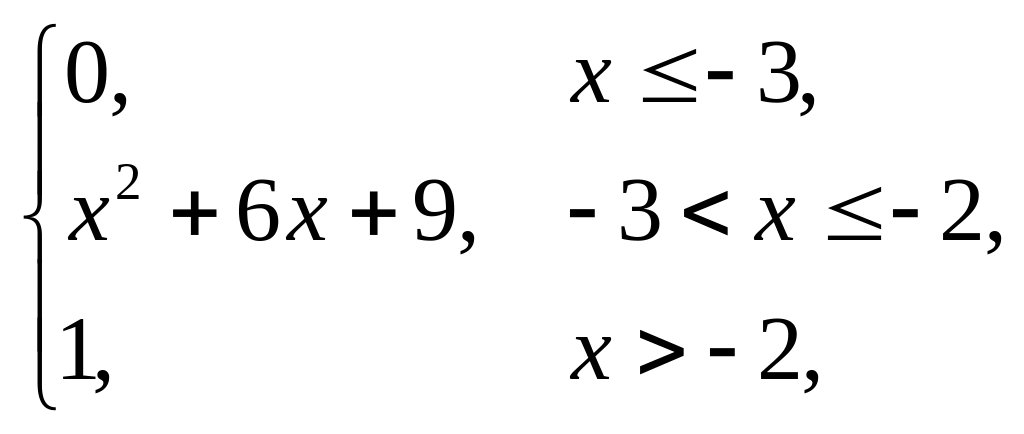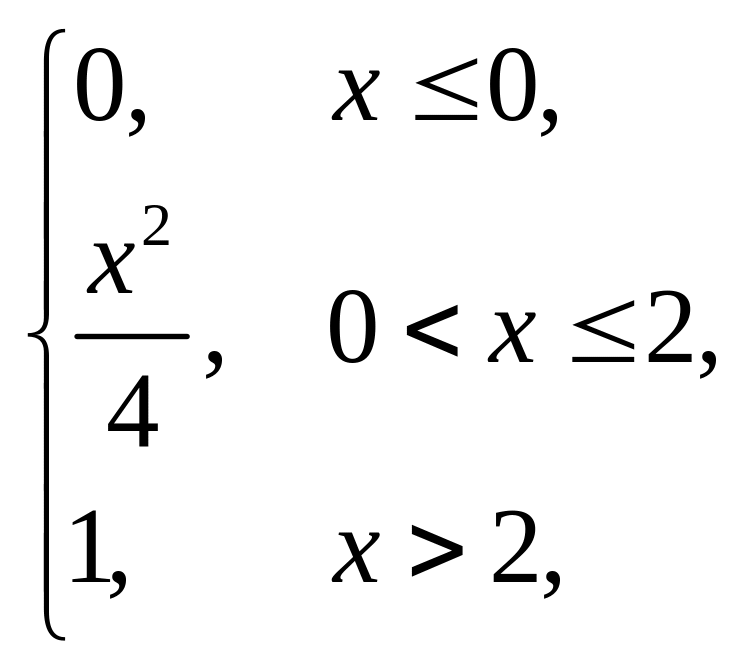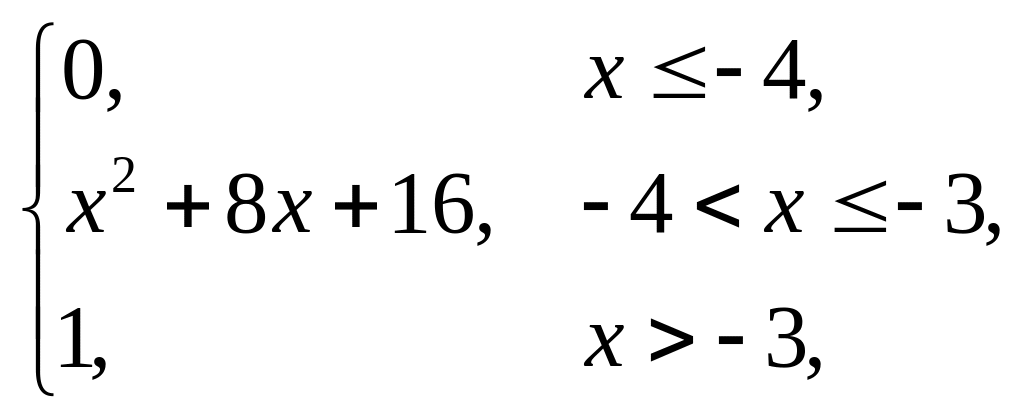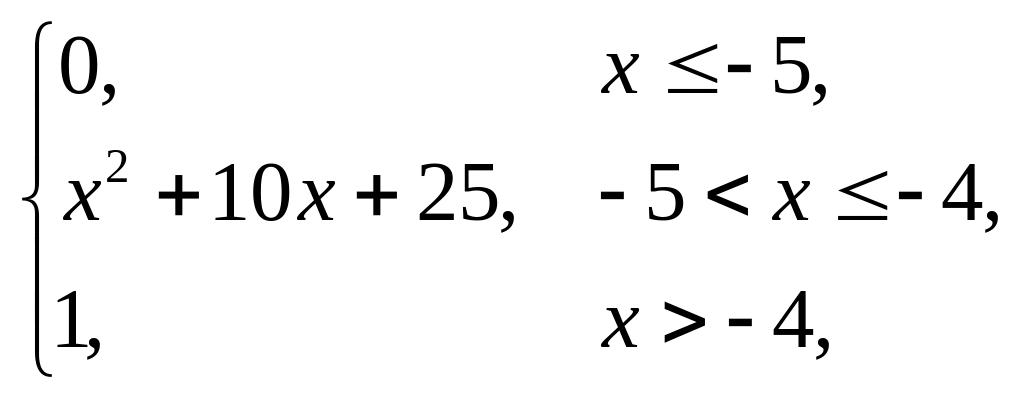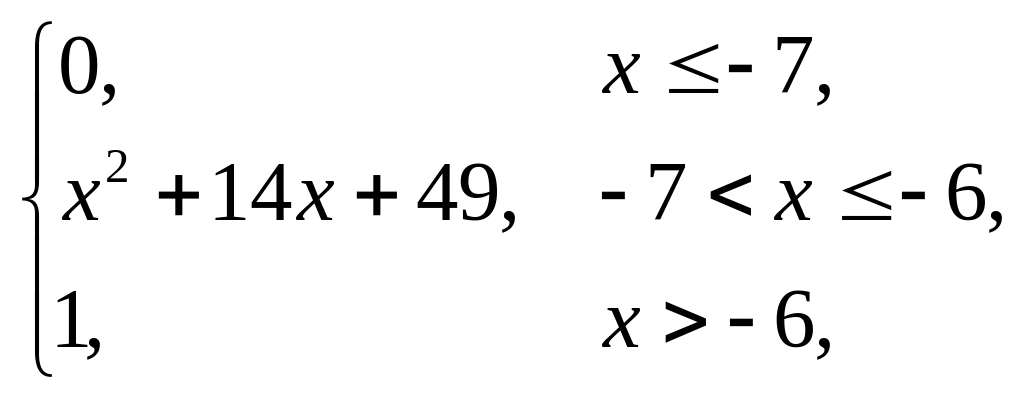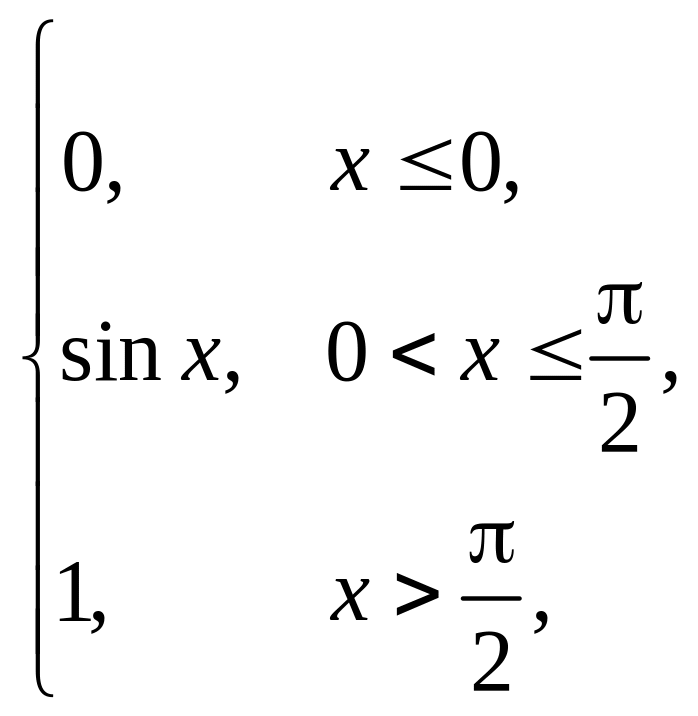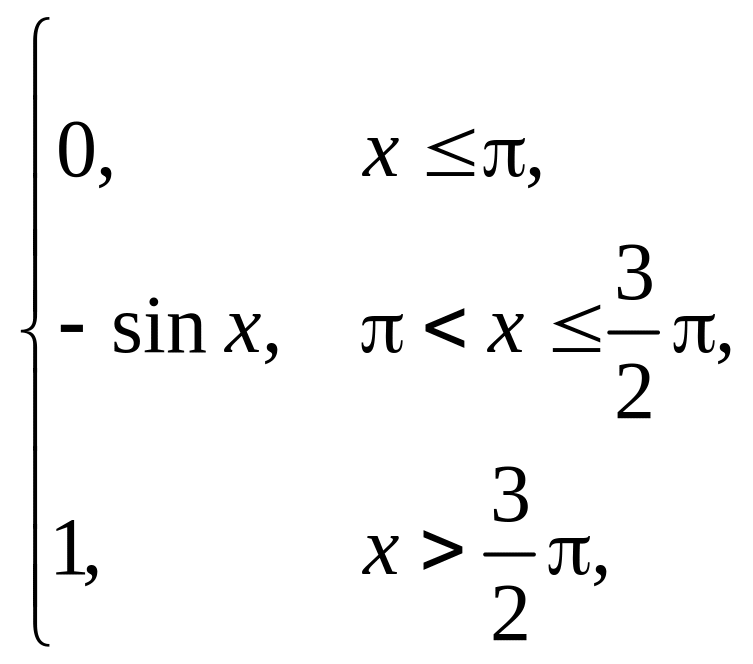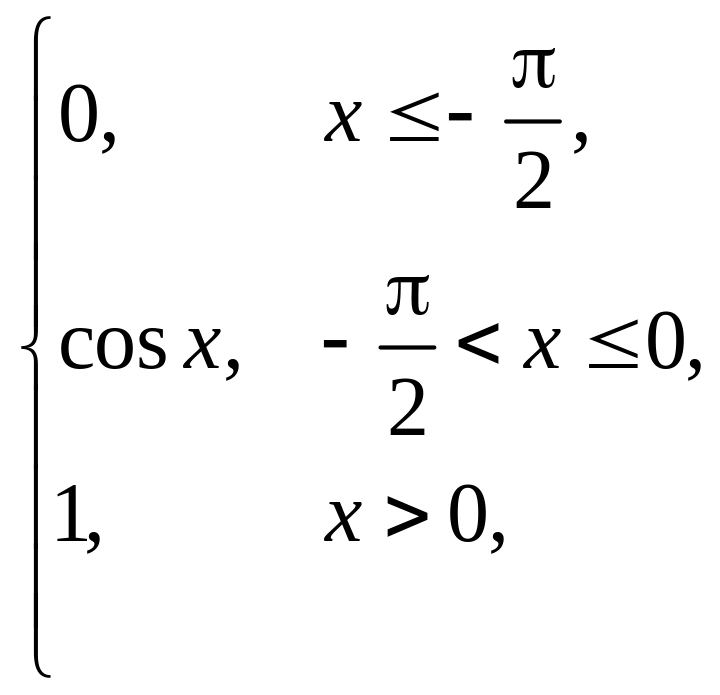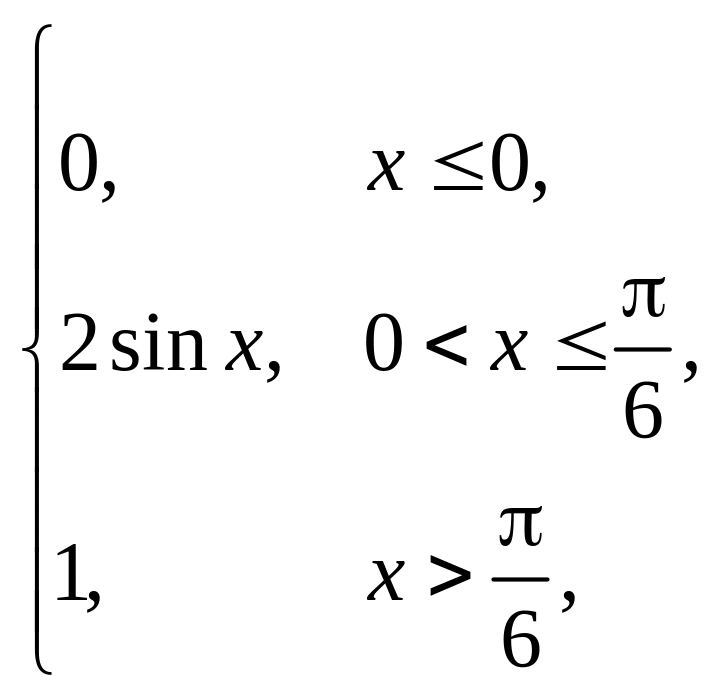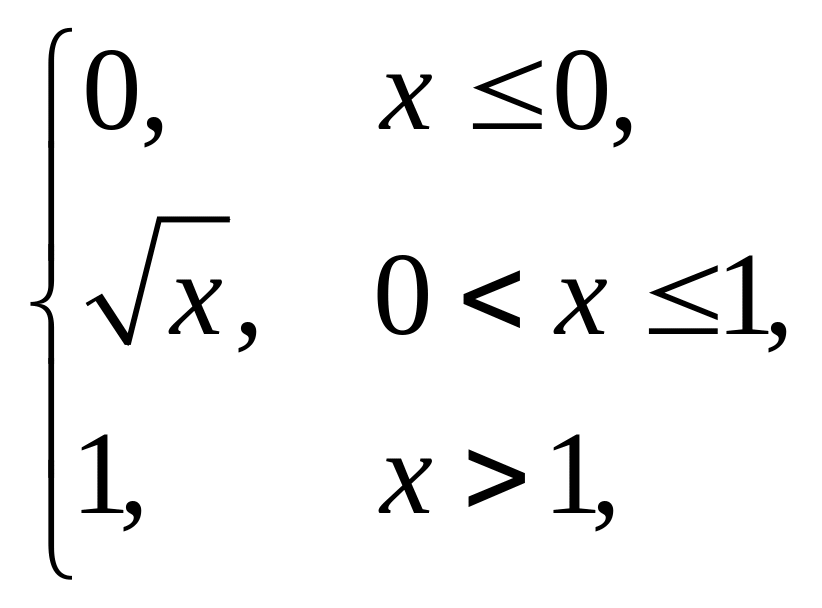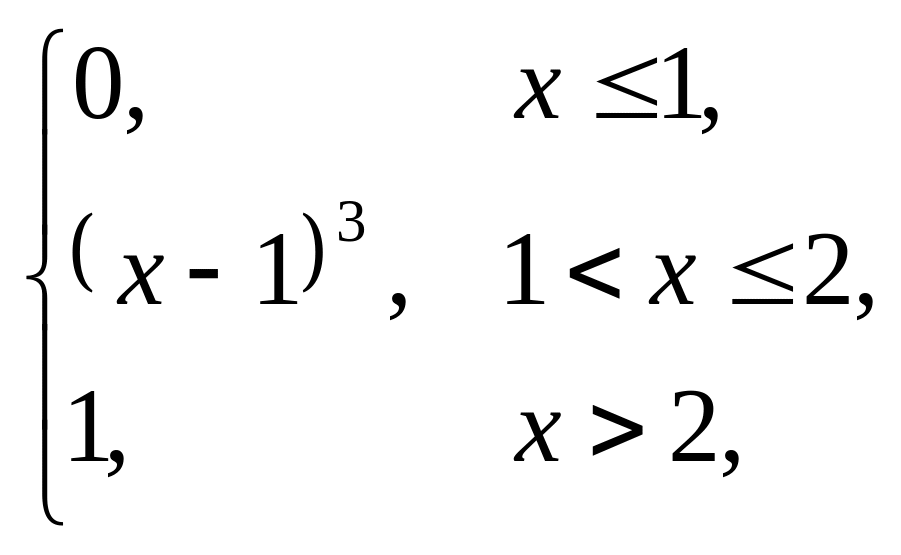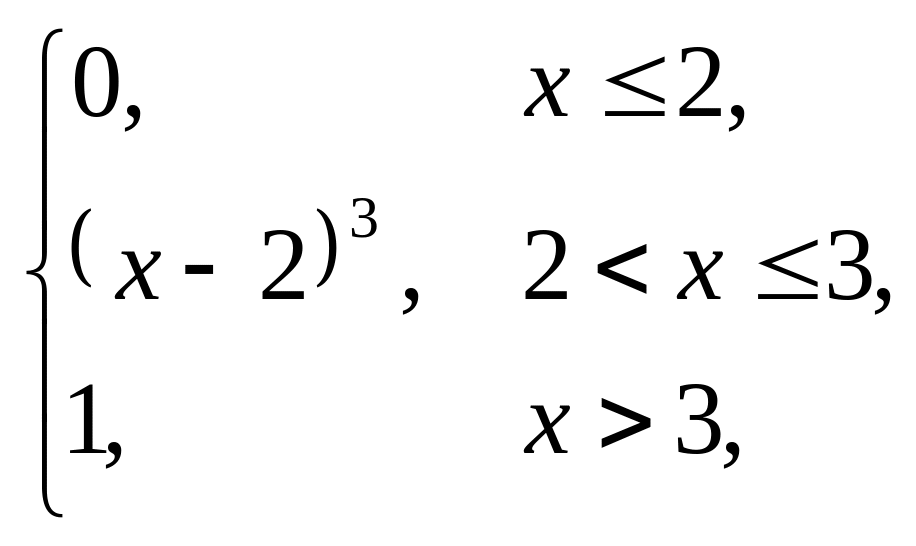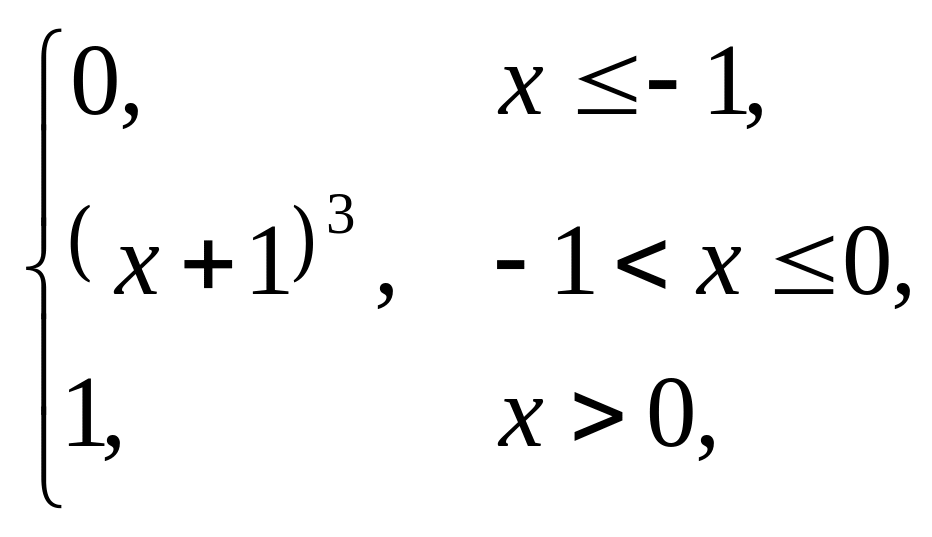Завдання 5
Випадкова величина x задана інтегральною функцією розподілу F(x). Знайти: густину розподілу ймовірності (диференціальну функцію f(x)); числові характеристики x (M(x), D(x), (x)); побудувати графіки інтегральної та диференціальної функцій; знайти ймовірність того, що випадкова величина прийме значення з проміжку (; ).
1. |
F(x) = |
(–0,5; 0,5). |
2. |
F(x) = |
(1,5; 3). |
3. |
F(x) = |
(1,5; 6). |
4. |
F(x) = |
(–3; –1). |
5. |
F(x) = |
(4; 6). |
6. |
F(x) = |
(2,5; 4). |
7. |
F(x) = |
(0; 11). |
8. |
F(x) = |
|
9. |
F(x) = |
(2,3; 4). |
10. |
F(x) = |
(2; 5). |
11. |
F(x) = |
(–0,5; 2). |
12. |
F(x) = |
(–4; 1). |
13. |
F(x) = |
(3; 5). |
14. |
F(x) = |
(3,5; 12). |
15. |
F(x) = |
(2; 7). |
16. |
F(x) = |
(–6; –0,3). |
17. |
F(x) = |
(–13; –1). |
18. |
F(x) = |
(2; 10). |
19. |
F(x) = |
(3; 19). |
20 |
F(x) = |
|
21. |
F(x) = |
(–4; 2,3). |
22. |
F(x) = |
(7; 16). |
23. |
F(x) = |
(3,3; 8). |
24. |
F(x) = |
(–3; 6). |
25. |
F(x) = |
(5; 18). |
26. |
F(x) = |
(–6; 13). |
27. |
F(x) = |
(5,4; 10). |
28. |
F(x) = |
(1; 9). |
29. |
F(x) = |
(2; 6). |
30. |
F(x) = |
(–2; 4). |
31. |
F(x) = |
(8,5; 10). |
32. |
F(x) = |
(3; 13). |
33. |
F(x) = |
(–7; 1,5). |
34. |
F(x) = |
(–0,5; 6). |
35. |
F(x) = |
(–2,3; 0). |
36. |
F(x) = |
(–6; 1). |
37. |
F(x) = |
(–3; 13). |
38. |
F(x) = |
(–16; –5,4). |
39. |
F(x) = |
(–10; –6,2). |
40. |
F(x) = |
(–6; 0). |
41. |
F(x) = |
|
42. |
F(x) = |
|
43. |
F(x) = |
|
44. |
F(x) = |
|
45. |
F(x) = |
(0,64; 2). |
46. |
F(x) = |
(0,5; 2). |
47. |
F(x) = |
(0; 0,5). |
48. |
F(x) = |
(2; 6). |
49. |
F(x) = |
(0; 2,2). |
50. |
F(x) = |
(–3,7; –0,5). |
Завдання 6
Вивчають витрати матеріалу під час виготовлення деякої деталі шляхом контролю маси відходів x. Враховуючи, що x — нормально розподілена випадкова величина з математичним сподіванням a і середнім квадратичним відхиленням , знайти: ймовірність того, що x набуде значення з інтервалу (; ); ймовірність того, що абсолютна величина відхилення x – a не перевищить .
|
a |
|
|
|
|
1. |
15 |
5 |
11 |
21 |
4 |
2. |
14 |
4 |
10 |
20 |
6 |
3. |
13 |
3 |
9 |
19 |
6 |
4. |
25 |
4 |
20 |
30 |
4 |
5. |
24 |
5 |
19 |
28 |
5 |
6. |
23 |
3 |
18 |
27 |
5 |
7. |
22 |
2 |
17 |
26 |
3 |
8. |
21 |
4 |
16 |
24 |
2 |
9. |
20 |
5 |
15 |
25 |
6 |
10. |
19 |
3 |
14 |
23 |
5 |
11. |
18 |
2 |
13 |
21 |
4 |
12. |
17 |
4 |
12 |
21 |
2 |
13. |
16 |
5 |
11 |
22 |
3 |
14. |
12 |
5 |
8 |
18 |
8 |
15. |
11 |
3 |
7 |
17 |
6 |
16. |
10 |
4 |
6 |
16 |
4 |
17. |
9 |
5 |
5 |
15 |
8 |
18. |
8 |
2 |
4 |
14 |
8 |
19. |
7 |
3 |
3 |
13 |
4 |
20. |
10 |
4 |
8 |
20 |
6 |
21. |
14 |
4 |
10 |
20 |
3 |
22. |
15 |
4 |
11 |
21 |
4 |
23. |
18 |
4 |
12 |
22 |
4 |
24. |
19 |
5 |
13 |
23 |
3 |
25. |
16 |
3 |
14 |
24 |
5 |
26. |
19 |
4 |
15 |
25 |
4 |
27. |
20 |
5 |
16 |
26 |
4 |
28. |
21 |
2 |
17 |
27 |
5 |
29. |
12 |
4 |
6 |
16 |
4 |
30. |
10 |
3 |
7 |
17 |
5 |
31. |
13 |
5 |
8 |
18 |
3 |
32. |
12 |
4 |
9 |
19 |
4 |
33. |
18 |
4 |
10 |
20 |
2 |
34. |
14 |
4 |
11 |
21 |
3 |
35. |
15 |
3 |
12 |
22 |
5 |
36. |
18 |
3 |
13 |
23 |
4 |
37. |
18 |
3 |
14 |
24 |
5 |
38. |
19 |
4 |
15 |
25 |
4 |
39. |
21 |
4 |
16 |
26 |
4 |
40. |
20 |
4 |
17 |
27 |
4 |
41. |
16 |
5 |
10 |
20 |
3 |
42. |
13 |
6 |
8 |
16 |
5 |
43. |
17 |
3 |
9 |
14 |
3 |
44. |
19 |
5 |
10 |
29 |
6 |
45. |
25 |
6 |
15 |
30 |
4 |
46. |
20 |
3 |
14 |
29 |
4 |
47. |
23 |
5 |
18 |
29 |
5 |
48. |
18 |
5 |
13 |
24 |
3 |
49. |
17 |
3 |
10 |
25 |
6 |
50. |
16 |
6 |
10 |
26 |
3 |