Хімічні реакції полімерів

1. Полімераналогічні перетворення

Термін "полімераналогічні перетворення" запропонував Г. Штаудінгер у 1934 році. Водночас відповідні реакції, такі, як нітрування целюлози або одержання полівінілового спирту, значно раніше використовували у промисловому масштабі.

Хімічні реакції у полімерних ланцюгах істотно відрізняються від відповідних перетворень низькомолекулярних речовин. Оскільки функціональні групи, що реагують, належать до одного ланцюга, то не можна відокремити цільові продукти від вихідних, і перетворення часто буває неповним, що може бути пов'язано й із суто статистичними причинами - утворенням ізольованих функціональних груп, як це буває під час одержання полівінілбутиралю з полівінілового спирту

або при внутрішньомолекулярній реакції Тищенка у поліакролеїні

Для таких реакцій, за розрахунками Флорі, максимально можливе статис тичне перетворення становить 86,5 %.

Неможливо довести до кінця реакції дегідратації полівінілового спирту та дегідрохлорування полівінілхлориду

В обох випадках у макромолекулах залишається значна кількість гідрок­сильних груп або атомів хлору. (Варто додати, що жодна з наведених вище типів реакцій не відбувається стовідсотково і для низькомолекулярних сполук).

Один з головних принципів полімерної хімії (принцип Флорі) - незалеж­ність реакційної здатності функціональної групи від розміру молекули, до якої вона приєднана. Водночас для виконання цього принципу необхідно, щоби реакція відбувалася у розбавлених розчинах (з мінімальною в'язкістю) за умови повної розчинності усіх компонентів системи. Необхідно також, щоб усі ділянки макромолекули були досяжними для низькомолекулярних реагентів.

Для більшості полімераналогічних перетворень усі ці умови не виконуються, тому для них принцип Флорі непридатний, і на практиці реакційна здатність функціональних груп у полімерному ланцюзі нижча, ніж у низькомолекулярних аналогів. Це явище називають "полімер-ефектом" і воно пов'язано з доступністю та взаємним впливом функціональних груп у ланцюзі макромолекули.

Доступність функціональних груп визначається насамперед стеричними перешкодами, які виникають у ланцюзі, якщо в ньому є додаткові об'ємні замісники. Наприклад, швидкість гідролізу поліметилакрилату па порядок більша від поліфенілметилакрилату

Вплив сусідніх функціональних груп може проявлятися як у сповільненні, так і у прискоренні реакцій з ними.

Ацетатна група, що розташована між двома гідроксилами, омилюється у 100 разів швидше від тієї, що між двома ацетатними групами. Це пояснюється адсорбцією йонів ОН^- на гідроксильних групах, що підвищує їхню локальну концентрацію в районі групи, що омилюється.

Прикладом впливу функціональної групи, що уповільнює процес, може слугувати гідроліз поліметакриламіду у лужному середовищі

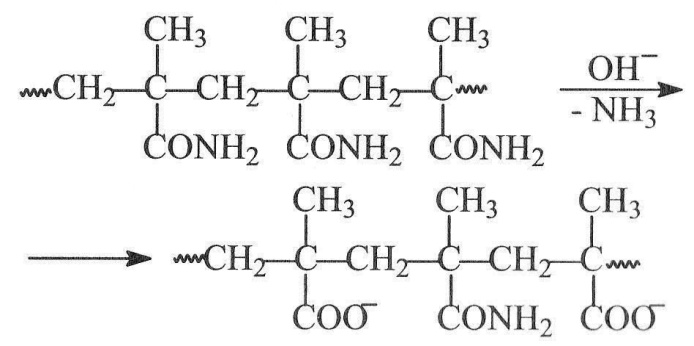
Поява поряд з амідною групою однієї, а тим більше двох карбоксилатних груп, перешкоджає підходу до неї гідроксид-аніонів. Через це ступінь конверсії реакції не може перевищувати 70 %.

Конфігураційний ефект. Швидкість полімераналогічного перетвореним залежить від просторового розташування лапок полімерного ланцюга. Наприклад, швидкості гідролізу ізо-, гетеро- та синдіотріад метилметакрилату

відносяться як 43 : 2,7 : 1. Проте здебільшого при полімераналогічних реакціях одного й того самого полімеру їхня швидкість зменшується у низці: ізо- > синдіо- > гетеро-.

Конформаційний ефект пов'язаний з гнучкістю макромолекули, тобто з її здатністю змінювати конформаційні форми. Для гнучких макромолекул доступність низькомолекулярного реагенту до функціональної групи буде значною мірою залежати від взаємодії полімеру з розчинником. У термодинамічно хороших розчинниках утворюються рихлі клубки, що полегшує проникнення у них низькомолекулярних реагентів і збільшує швидкість їхньої взаємодії з функціональними групами. Протилежний ефект буде у термодинамічно поганому розчиннику, де утворюються щільні малопроникні клубки.

Отже, вплив конформаційного ефекту можна визначити, здійснюючи ту саму реакцію у розчинниках з різною термодинамічною якістю.

Надмолекулярний ефект може проявитися лише для гетерогенних полімераналогічних реакцій, коли їхня швидкість залежить від ступеня орієнтації та упакування макромолекул. Для кристалічного та аморфного полімеру однакової хімічної будови швидше буде реагувати аморфний. Так менш кристалічний та розгалужений поліетилен високого тиску набагато швидше хлорується та окиснюється, ніж лінійний поліетилен низького тиску.

Велика кількість "полімерних" ефектів, які супроводжують полімераналогічні реакції, значно ускладнює їхні кінетичні дослідження. Однак можна створити умови, що зводять до мінімуму згадані ефекти. Так, під час реакцій у розбавлених та термодинамічно хороших розчинниках з полімерами, які не мають об'ємних груп, практично єдиним чинником, який впливає на швидкість процесу, залишається ефект сусідніх груп. Досліджуючи за таких умов реакції естерифікації та гідролізy полімерів акрилового ряду, професор Московського університету академік Микола Альфредович Плате (нар. 1914 р.) розробив кінетичну модель, що добре збігається з експериментальними даними. Зобразимо полімераналогічне перетворення схемою, де групи А перетворюються на групи В за необоротною реакцією першого порядку

- А -В

- А -В

- А → -А

- А -В

- А -А

- А -В

Розглянемо такі можливі послідовності функціональних груп у полімер­ному ланцюзі -AAA-; -BAA- та -ВАВ-. Реакційна здатність груп А у тріадах різна і характеризується константами швидкості відповідно к₀; к₁; к₂.

У разі прискорювального впливу сусідніх груп к₀ < к₁ < к₂. При уповільненні процесу буде зворотна низка к₀ > к₁ > к₂. Для визначення частки груп А, що не прореагували за час t у полімері Р[А], М. А. Плате зі співробітниками запропонували таке рівняння:

Р[А] = ехр(- 2k₂t){2(k₂ – k ₁)expX · ∫exp (k₂ - 2k₁)t · exp[Yexp(- k₀t)]dt +

+ (2k₁ – k₀ - k₂)expX · ∫exp (k₂ – k₀ - 2k₁)exp[Yexp(- k₀t)dt + C},

де X = 2(k₀ – k₁)/t; Y = 2(k₀ – k₁)/k₀; С - константа інтегрування.