Postupivuz.ru Postupivuz.ru Postupivuz.ru

Подготовка к ЕГЭ или что вас ждёт на экзамене.

Самые свежие материалы из банка заданий mathege.ru, из которых будут формироваться варианты ЕГЭ. Предлагаем тест, составленный из заданий B1 – B12 с подробным решением.

Задания B1

№ 1. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы, кратные 10 рублям. Лена хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приёмное устройство данного терминала?

Решение: Вычислим 5% с 300 рублей. 300*5:100 = 3*5 = 15 рублей. Чтобы компенсировать эти 15 рублей их надо добавить к 300 рублям, но 300+15 =315 не кратно 10, возьмем ближайшее число: Чтобы компенсировать эти 15 рублей, их надо добавить к 300 рублям, но 300+15 =315 не кратно 10, возьмем ближайшее число 320.

Проверим . 320*5% = 320:100*5 = 16 рублей. 320-16 = 304 рубля > 300.

№ 2. Торговая фирма закупила 65 автомобилей по средней цене 450 тыс. рублей. Средняя цена продажи автомобиля составила 495 тыс. рублей, при этом накладные расходы фирмы по этой партии товара составили 225 тыс. рублей. Какую прибыль (в тыс. рублей) получила фирма?

Решение: Найдем, какую прибыль фирма получила с одного автомобиля: 495 – 450 = 45  (тыс.руб.) Найдём прибыль за 65 автомобилей: 45*65=2925 (тыс. руб.) Вычтем накладные расходы: 2925 – 225 = 2700 - прибыль. Ответ: 2700

Примечание: Обязательно учитывайте, в каких единицах давать ответ (в тысячах или в рублях).

Задания b2

№1. На графике, изображенном на рисунке, представлено изменение биржевой стоимости акций горнодобывающей компании в первой половине сентября. 7 сентября бизнесмен купил пакет акций, а 13 сентября продал его. В результате этих операций прибыль бизнесмена составила 3600 рублей. Сколько акций было в пакете?

Решение: 7 сентября одна акция стоила 300 руб., 13-го сентября – 600 рублей.

Прибыль с одной акции составила 600-300 = 300 рублей. Всю прибыль делим на прибыль с одной акции, получаем количество купленных акций: 3600 : 300 = 12 акций. Ответ: 12.

№ 2. На графике изображена зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат – крутящий момент в Н м. Чтобы автомобиль начал движение, крутящий момент должен быть не менее 60 Н м. Какое наименьшее число оборотов двигателя в минуту достаточно, чтобы автомобиль начал движение?

Решение: На оси у выбираем точку 60. Из неё проводим прямую параллельно оси об/мин до пересечения с графиком. Из этой точки опускаем перпендикуляр на ось об/мин. Попадаем в точку 2000. Ответ: 2000.

Задания b3

№ 1. Найдите корень уравнения: log _½ (2-3x) = -5

Решение: 2-3x = (1/2)^-5 ; 2-3x= 2⁵ ; 2-3x = 32; -3x = 30; x=30 : (-3); x= -10. Ответ: -10.

Примечание: если получите 2 решения, то обязательно!!! сделайте проверку.

№ 2. Решить уравнение: (x² -9) / (x+3) = 0,3.

Решение: Заметим, что х+3 ≠ 0, т.е. х ≠ -3. (х-3)(х+3) / (х-3) = 0,3; x+3 = 0,3; x= -2,7.

Ответ: -2,7.

№ 3. Найти наибольший отрицательный корень уравнения: cos п(4х-7)/3=1/2.

Решение

п(4х-7)/3 = ±п/3 + 2пk    -->   (4х-7)/3 = ±1/3 + 2k   -->  4х-7 = ±1 + 6k  -->  x=(7±1 +6k)/4.

При k=0,1,2...   x>0.       Пусть k=-1, тогда х=(7±1-6)/4  -->  x=1/2 или x=0.

Пусть k=-2, тогда х=(7±1-12)/4   -->   x=-1 или х=-3/2 и т.д.  

Наибольший отрицательный корень х=-1.

Задание B4. В треугольнике ABC AC = BC, AH - высота, sin BAC = 4/√17. Найти tg BAH.

Угол CAB = углу CBA = α , угол ВАН= 90°- α

tg угла BAH = tg (90° - α) = ctg α           Воспользуемся ф-лой: 1+ 1/ctg²α = 1/ sin²α   

1/ctg² α = 17/16 - 1 = 1/16;    ctg² α =16;    ctg α = 4   (a -острый угол, поэтому берем +4)

Ответ: 4

Задания B5

№ 1. При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 10 тонн природного камня и 11 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1400 рублей, щебень стоит 670 рублей за тонну, а мешок цемента стоит 220 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?

Решение:

Для каменного фундамента: 10 тонн камня*1400р + 11 мешков цем.* 220р = 14000+2420=16420

Для бетонного : 7 тонн щебня *670р + 50 мешков цем. * 220р = 4690+11000 = 15690 

Ответ:   15690

№ 2. Для изготовления книжных полок требуется заказать 20 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,35 м². В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?

Фирма	Цена стекла (руб. за 1 м2).	Резка и шлифовка (руб. за одно стекло)
A	420	75
Б	440	65
В	470	55

Решение. Общая площадь стекол = 20 x0,35 =7 кв.м 

А: 7 * 420р + 75р * 20 стекол = 2940 + 1500 = 4440

Б: 7 * 440 + 65 * 20 = 3080 + 1300 = 4380

В: 7 * 470 + 55 * 20 = 3290 + 1100 = 4390 Ответ:     4380

Задания B6

№1. Найдите площадь четырехугольника, вершины которого имеют координаты (6;5), (9;6), (10;9), (7;8).

Решение.             

Постройте по заданным точкам 4-к, а затем обрисуйте его прямоугольником и от площади прямоугольника отнимите площади четырех треугольников.

S ромба = S квадрата - 4Sтреугольников = 4*4 - 4*(4*1/2) = 16-8 = 8 Ответ: 8

№ 2. Меньшее основание равнобедренной трапеции равно 6. Высота трапеции − 10. Тангенс острого угла равен 2. Найдите большее основание трапеции.

Обозначим CP = KD = x.

В 3-ке ACP: tg C = AP/CP = 10/x = 2  →  x/10 = 1/2   → x = 5.    CD = 5+6+5 = 16. Ответ: 16

Задания B7

№ 1. Найдите значение выражения , если .

Решение. log_a(ab³) = log_a a + 3log_ab = 1 +3 / log_b a = 1 + 3/(1/7) = 1 + 3*7 = 22. Ответ: 22.

№ 2. Найдите значение выражения при .

Решение. a ^1/9_*a ^1/18 / (a*a ^1/6) = a ^3/18 / a ^7/6 = a ^1/6 / a ^7/6 = a ^{1/6 – 7/6} = a^-1 = 1/a = 1/1,25 = 1/ (5/4) = 4/5 = 0,8 Ответ: 0,8.

Задания B8

№1. Прямая у = 7х – 5 параллельна касательной к графику функции . Найдите абсциссу точки касания.

Решение. у' = 7; у' = 2х +6. 2х+6 = 7; 2х = 1; х = 0,5. Ответ: 0,5.

№ 2. На рисунке изображен график производной функции , определенной на интервале . Найдите промежутки возрастания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.

Решение. Функция возрастает на промежутке, на котором производная положительна.

(-7; -5,5); (-2,5; 4). Целые точки на этих промежутках: -6, -2, -1, 0, 1, 2, 3, а их сумма равна -3.

Ответ: -3.

Задания B9

№ 1. Объем конуса равен 64. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Решение:  объем большого конуса V1 равен  πR²H/3 = 64    

В маленьком конусе: r = R/2,   h=H/2

V малого конуса = π (R/2)² · (H/2) /3 = πR²/4 ·H/2/3 = πR²H/3 /8 = 64/8 =  8

Ответ: 8

№ 2. Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

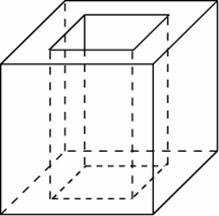S куба = 6а² =6*1² = 6 – сумма площадей 6-ти граней. Вычтем площади двух квадратиков со сторонами 0,5 (площади отверстий). S_ =2*0,5² =2*0,25 = 0,5 Прибавим 4 площади прямоугольников, которые лежат внутри куба Sвнутр = 4* 1*0,5 = 2.

Получим: S= 6 – 0,5 +2 = 7,5. Ответ: 7,5.

№ 3.. В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.

V1 = Sосн*h = 6 – первоначальный объем жидкости.

V2 = Sосн* 1,5h = 1,5 V1 = 1,5*6 = 9 – объем после поднятия уровня в 1,5 раза.

V детали = V2 – V1 = 9-6 =3. Ответ: 3.