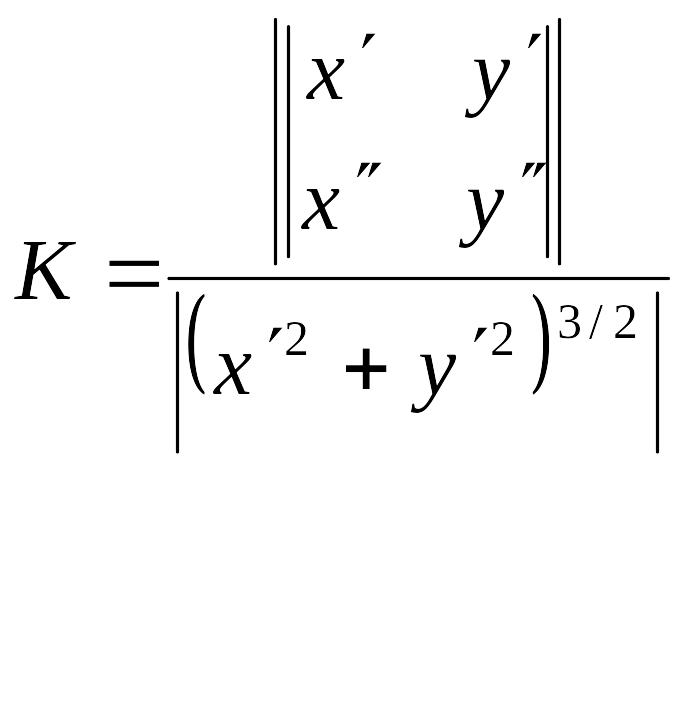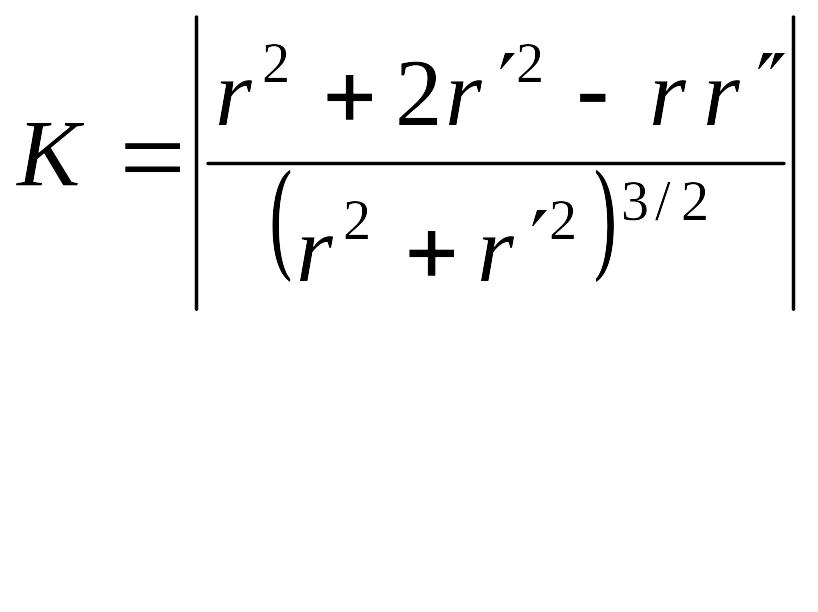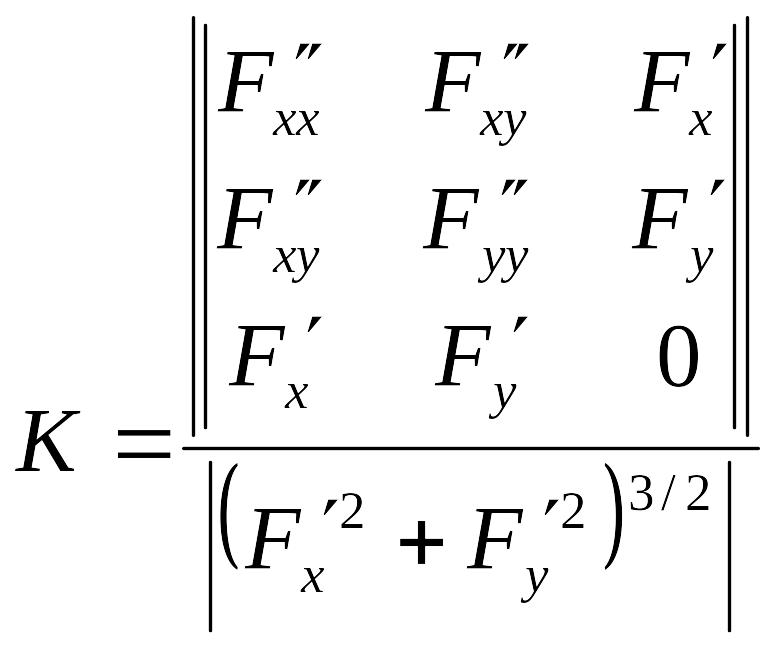Вычисление дифференциала. Правило Лопиталя.

Цель:

1) изучить понятие дифференциала;

2) научиться вычислять производные по правилу Лопиталя

Правила Лопиталя раскрытия неопределённостей.

,

,

.

.

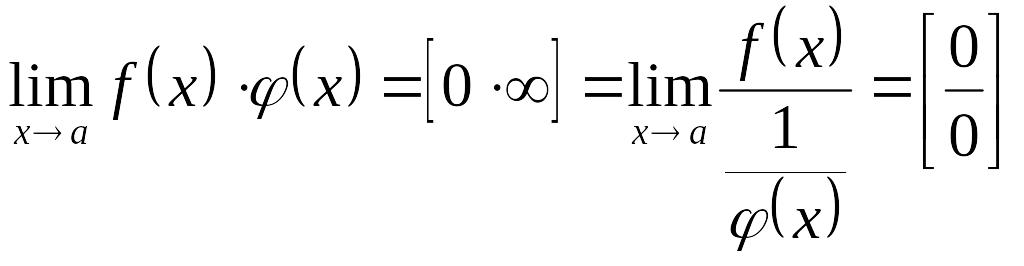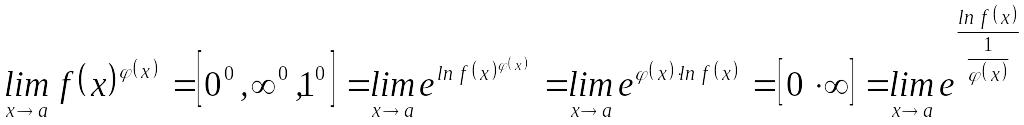I. Вычисление дифференциала

Пример 1. Найти дифференциал функции .

Так как то в данном случае

II. Правило Лопиталя

Пример 2. Найти пределы, используя правило Лопиталя:

1.

Решение:

1) Поскольку lnsin3x и lnx стремятся к бесконечности при x→0, то в данном случае имеем неопределенность вида

Применяя правило Лопиталя, получим

В последнем равенстве мы воспользовались первым замечательным пределом.

2.

Решение:

поэтому имеем неопределенность вида Воспользуемся правилом Лопиталя:

В этом примере правило Лопиталя применялось дважды.

3.

Решение:

Здесь имеет место неопределенность вида , которую мы раскроем, предварительно сведя ее к неопределлости ; а далее воспользуемся правилом Лопиталя:

4.

Решение:

Имеем неопределенность . Сведем ее к неопределенности , приведя дроби к общему знаменателю:

Правило Лопиталя в этом примере применялось дважды.

5.

Решение:

В этом случае имеем неопределенность вида . Неопределенности этого вида, также как и неопределенности вида , , можно найти, предварительно вычислив предел от логарифма функции.

Итак, обозначим y=x^x. Тогда

Таким образом,

откуда т.е.

6.

Решение:

Здесь неопределенность вида . Обозначив , найдем

Отсюда т.е.

Вычислить пределы, используя правила Лопиталя.

1. ; 2. ; 3. ; 4. ;

5. ; 7.

Ответы: 1) 9 ; 2) ; 3) ; 4) 0,5 ; 5) ; 6) 1.

Исследование функций и построение графиков.

Цель: изучить приложения производных и научиться применять их при решении задач

Приложение производной

Промежутки монотонности

Промежутки монотонности определяются с помощью первой производной

f(x) >0, f(x) возрастает,

f(x) <0, f(x) убывает

f(x) =0, х – критическая точка или f(x) не существует.

Промежутки выпуклости и вогнутости

Направление выпуклости и точки перегиба функции y = f(x) определяются с помощью второй производной.

y >0, то f(x) вогнута,

f(x) = <0, то f(x) выпукла

f(x) =0, х – критическая точка или f(x) не существует.

Асимптоты функции

Асимптота функции y = f(x) есть прямая.

Вертикальная асимптота х = a, если .

Горизонтальная асимптота y = b, если

Наклонная асимптота y = kx +b , .

Вектор-функция

.

Годограф

Годографом называется линия, описываемая концом вектора .

– скорость, направленная по касательной к годографу.

– ускорение.

Кривая

Кривизна y = f(x) в точке M0

кривая, заданная в декартовой системе координат	Кривая, заданная параметрически	кривая, заданная в полярной системе координат	Кривая, заданная неявно
y = f(x)		в) r = r()	F(x; y) = 0