Содержание

Модуль 5 Дифференциальное исчисление функций одной переменной 5

Правила нахождения производных 5

Геометрический и физический смысл производной. Касательная и нормаль 9

Вычисление дифференциала. Правило Лопиталя. 12

Исследование функций и построение графиков. 14

Модуль 6 Интегральное исчисление функций одной переменной. Неопределенный интеграл 19

Понятие неопределенного интеграла. Таблица интегралов 19

Интегрирование элементарных и рациональных дробей 22

Интегрирование тригонометрических функций 25

Интегрирование некоторых иррациональных функций 27

Модуль 7 Интегральное исчисление функций одной переменной. Определенный интеграл 30

Вычисление определенных и несобственных интегралов. 30

Геометрическое приложение определенных интегралов. 36

Модуль 8 Дифференциальное исчисление функций нескольких переменных 40

Частные производные 40

Производные сложной функции. Экстремумы. 43

Список литературы 46

Модуль 5 Дифференциальное исчисление функций одной переменной Правила нахождения производных

Цель: научить применять правила нахождения производных.

Определение производной

Правила дифференцирования

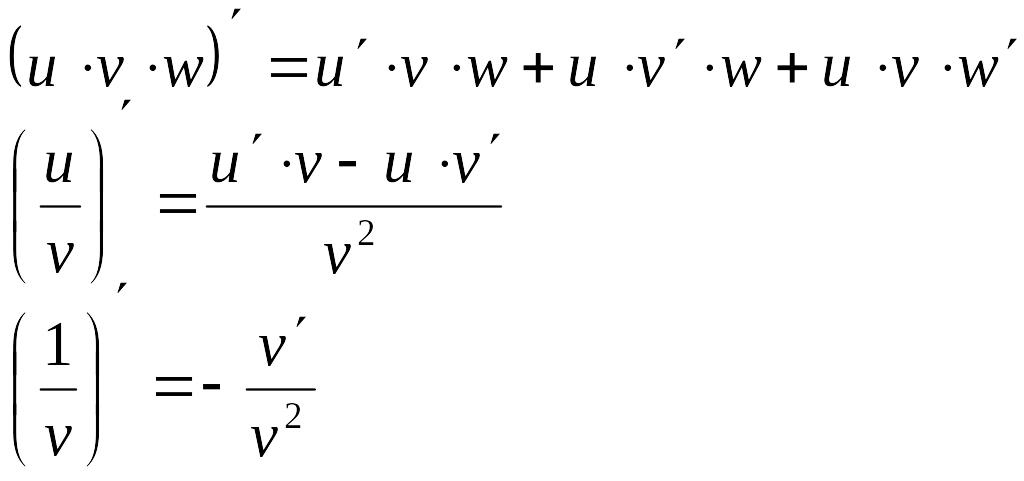
Таблица производных

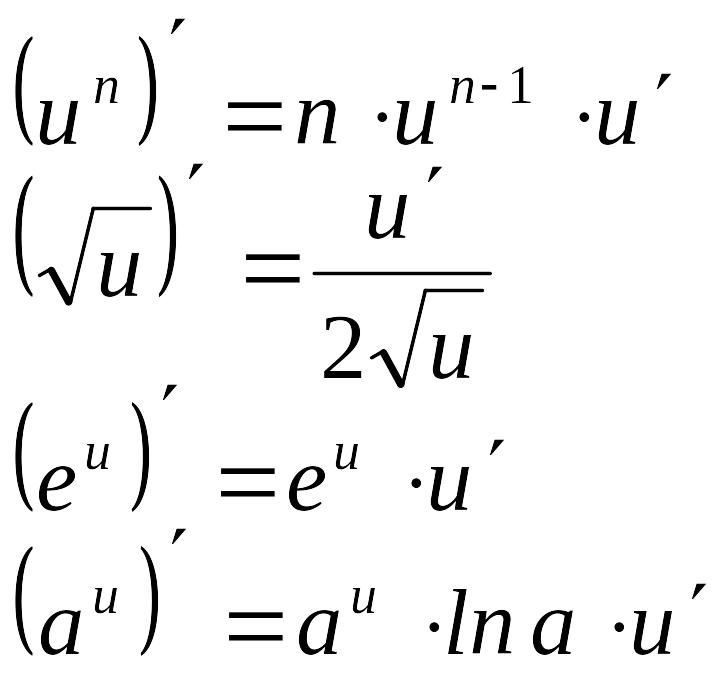
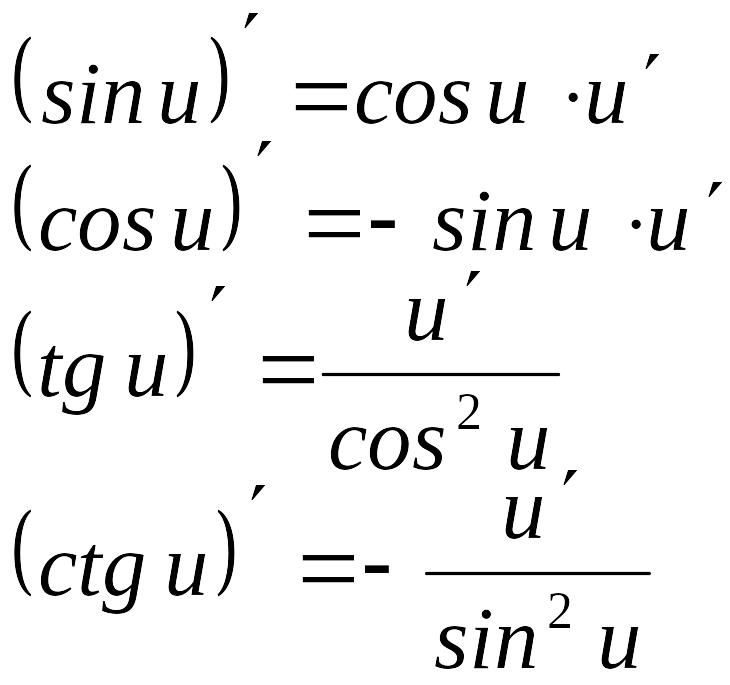
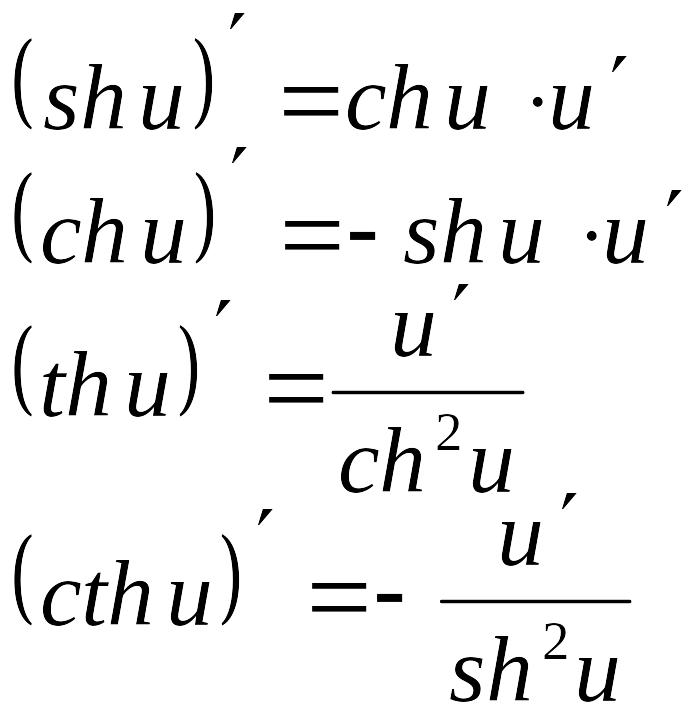
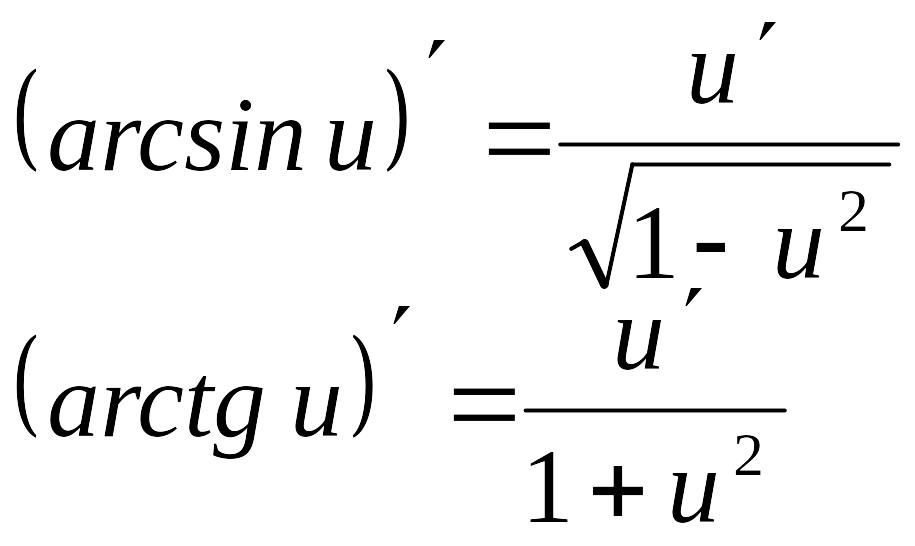
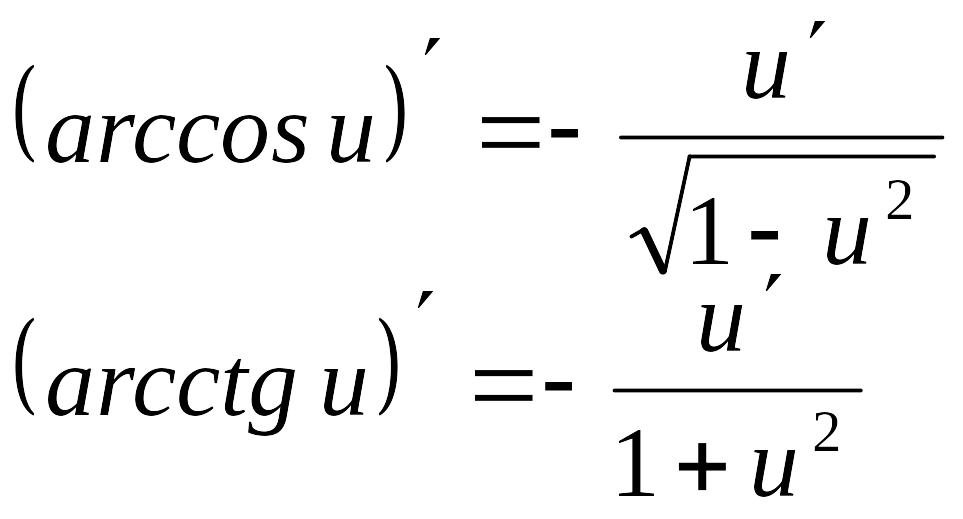
Производная сложной функции

.

Производная функции, заданной неявно

Дифференцируется левая часть как сложная функция, и полученное уравнение разрешается относительно .

Производная функции, заданной параметрически

: , .

Пример 1. Пользуясь определением, найти производную функции y=f(x):

1) y=3x²; 2) y=sinx.

Решение:

1) Придадим аргументу x приращение Δx. Тогда соответствующее приращение Δy функции имеет вид Δy=f(x+ Δx)-f(x)=3(x+ Δx)²-3x²=3(x²+2xΔx+(Δx)²-x²)=3Δx(2x+ Δx).

Отсюда находим предел отношения в точке x при Δx→0:

Таким образом,

2) Найдем приращение Δy функции, соответствующее приращению Δx аргумента, используя формулу разности синусов:

Отсюда

В последнем равенстве мы воспользовались первым замечательным пределом и непрерывностью cosx. Таким образом,

Пример 2. Пользуясь основными правилами дифференцирования, найти , если :

1) 2) f(x)=(x⁴-x)(3tgx-1).

Решение:

1) Преобразуем функцию к виду

Отсюда, используя таблицу производных, получим

2) Воспользуемся формулой для производной произведения:

Пример 3. Применяя правило дифференцирования сложной функции, найти производную функции y: 1) y=sin²x; 2) y=ln(arctg3x).

Решение:

1) Данная функция y=sin²x является композицией двух имеющих производные функций u=sinx и f(u)=u². Так как то с учетом правила дифференцирования сложной функции получим:

2) Функция ln(arctg3x) – композиция функций u=arctg3x и f(u)=lnu, откуда

Функция arctg3x, в свою очередь, является композицией двух функций v=3x и g(v)=arctgv, поэтому для нахождения ее производной нам придется еще раз применить правило дифференцирования сложной функции:

Отсюда окончательно

Пример 4. Используя логарифмическую производную, найти производные функций:

1) y=x^sinx; 2) y=

Решение:

1) Прологарифмируем обе части равенства y=x^sinx. Тогда lny=lnx^sinx, т.е. lny=sinxlnx. Теперь продифференцируем последнее равенство, при этом в левой части используем производную сложной функции, а в правой – производную произведения:

Отсюда или, учитывая, что y=x^sinx, .

2) Непосредственное дифференцирование данной дроби привело бы к громоздким вычислениям, зато применение логарифмической производной позволяет найти ответ без труда:

Отсюда, используя формулы для логарифма произведения, частного и степени, получим:

Осталось продифференцировать обе части полученного равенства:

Пример 5. Найти производную неявно заданной функции y: x³+y³=sin(x-2y).

Решение:

Дифференцируя обе части уравнения и учитывая, что y – есть функция от x (поэтому, например,

получим:

Отсюда находим

б

т.е.

Пример 6. Найти производную от следующей функции, заданной параметрически: x=2cost, y=3sint.

Решение:

Производная функции y(x) находится по формуле откуда в нашем случае

Выполнить самостоятельно:

Найти производную следующих функций:

а) ; б) ; в) y = ctg ³ ; г) ;

д) y = ln(ln ²(ln ³ x)); е) ; ж) ; з) y = (ctg  x) ^{sin ( x – 1)}; и) ; к) ; л) xarcsin y = yarcsin x; м) ; н) ; о) при t > 0.