Правила знаходження точок перегину.

1.Знайти другу похідну f″(x) і прирівняти її до нуля.

2.Розв’язати одержане рівняння f″(x) = 0 і розташувати корені у порядку зростання. До них дописати точки, в яких друга похідна не існує. Отримали критичні точки на перегин: .

3.Обчислити значення другої похідної лівіше і правіше кожної з критичних точок. Якщо при переході через дану критичну точку f″(x) змінює знак, то перегин є, якщо не змінює, то перетину нема.

4.Обчислити значення функції в точках перегину.

Загальна схема побудови графіка функції.

1.Знайти область визначення функції.

2.Встановити, чи являється дана функція парною чи непарною.

3.Знайти точки перетину графіка з осями координат.

4.Знайти асимптоти графіка функції

5.Знайти екстремум функції.

6.Знайти точки перегину функції.

7.Знайти координати додаткових точок.

8.За одержаними даними побудувати графік.

Приклад 10.

Побудувати схематичний графік функцій:

Розв’язання.

1) Дана функція визначена на всій числовій прямій, тобто

2) Знайдемо:

звідси видно, що вона не відноситься ні до парних, ні до непарних, тобто вона індефферентна.

3) Знайдемо точки перетину функції з віссю ОУ, для цього покладемо х = 0, тоді у = -3. Тобто, функція перетинає вісь ОУ в точці (0:-3). Точки перетину графіка з віссю ОХ знайти важко, бо виникають труднощі при розв’язанні рівняння .

4) Очевидно, що графік функції немає асимптот.

5) Знайдемо похідну , прирівняємо її до 0 і розв’яжемо рівняння:

Маємо - критичні точки.

Екстремум будемо знаходити за другим правилом.

Тому , і обчислимо

в точці х = 1 функція має max.

в точці х = 3 функція має min.

Для зручності ці дані і слідуючи занесемо в таблицю:

х	0	1	2	3	4
		0		0
Y”		-6	0	6
у		Max 1	Пере-гину -1	Min -3

6) Знайдемо точки перегину:

у”=6х-12 6х-12=0

6х=12, х=2 – критичні точки на перегин.

З таблиці видно, що при переході через дану точку друга похідна змінює знак, тобто перегин є.

7) Знайдемо додаткові точки при х=0 і при х=4.

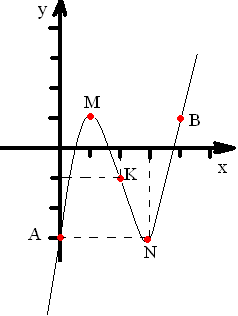
8) З даними таблиці побудуємо графік:

M(1:1)- точки max.

N(3:-3)- точки min.

K(2:-1)- точки перегину.

A(0:-3), В(4:1)- Додаткові точки.

За даними дослідження побудуємо графік