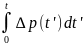ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО

ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА ИМЕНИ И.М. ГУБКИНА» в г. ОРЕНБУРГЕ

Отделение «Разработка, проектирование, эксплуатация нефтяных месторождений, газопроводов и газонефтехранилищ»

КУРСОВАЯ РАБОТА

по курсу «Подземная гидромеханика»

на тему «Расчет параметров вытеснения при заданном

перепаде давления на границах пласта»

Выполнил: ст. гр. РГ-10

Бакиева А.В.

Проверил: к.т.н., доцент

Цвяк.А.В.

Оренбург 2013

Содержание

1. Расчет параметров вытеснения при заданном перепаде давления

на границах пласта………………………………………..…………………………3

2. Лабораторные измерения функций, определяющих процесс вытеснения…...7

3. Нахождение вида функции f(s) по интегральным характеристикам, измеренным в экспериментах……………………………………………………….8

4. Определение относительных фазовых проницаемостей………………………9

5. Список используемой литературы……………………………………………...11

1.Расчет параметров вытеснения при заданном перепаде давления

на границах пласта

До сих пор рассматривались задачи вытеснения в предположении, что известна суммарная скорость фильтрации w(f) (или расход) фаз. Техноло­гия процесса заводнения такова, что чаще бывает известен перепад давле­ния 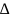р, под действием которого вода вытесняет нефть. Поэтому представ­ляет интерес обобщить полученные результаты на этот случай и исследо­вать динамику обводения продукции на примере прямолинейно- парал­лельного вытеснения (см. рис. 1).

Рис. 1. Профили насыщенности при прямолинейно-параллельном вытеснении

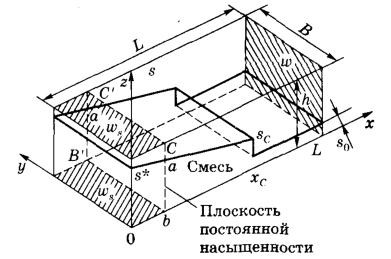
Пусть в начальном сечении х = 0 и на выходе из пласта х = L заданы давления p₀(t) и p_L(t), так что движущий перепад давления

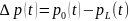
Складывая почленно равенства, выразим градиент дав­ления в зоне смеси:

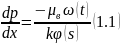
Где введено обозначение

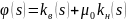, а

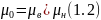
Рассмотрим первую фазу вытеснения, когда фронт не достиг вход­ного сечения пласта (х < L, см. рис.1). Тогда перепад давления в об­ласти, занятой смесью, после интегрирования уравнения (1) по зоне смеси определится по формуле

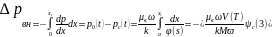
Где

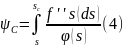
а техника преобразования второго интеграла (3) к виду (4) .

Перепад давления между фронтом и добывающей галереей Δр_н нахо­дится в результате интегрирования уравнения (1) по области, занятой нефтью (х_с < х < L). При этом следует иметь в виду, что в этой области

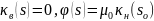, где 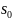-постоянная начальная водонасыщенность. Тогда из (1) получаем:

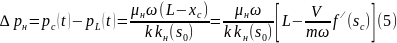
где было использовано равенство, 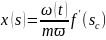заменившее х_с.

Складывая почленно соотношения (3) и (5) и учитывая предыдущее равенство, получаем:

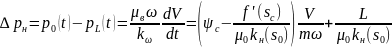
Разделив здесь переменные и проинтегрировав, окончательно най­дем:

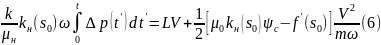
(0 < t < t°), где t° - время прорыва воды, определяемое из (6) после подстановки V = V(t°) согласно формуле

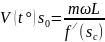; t' - переменная интегрирования по времени.

Левая часть уравнения (6) известна, поскольку задан перепад давления. Тогда положительный корень этого квадратного уравнения оп­ределяет V(t), а затем находят дебит Q = dV/dt как функцию времени. Этими формулами можно пользоваться до момента прихода фронта х_с к конечному сечению пласта. На этой стадии в добывающую галерею посту­пает безводная нефть (V = V_H,Q = Q_H).

После прорыва воды (х_с > L, t > t°) - вторая фаза вытеснения - сле­дует интегрировать уравнение (1) по зоне смеси в интервале О < х < L. В результате получится соотношение, аналогичное (3), где верхним пределом интегрирования в функции 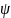(см. 4) нужно при­нять значение 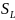, определяемое из формулы

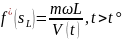
После замены w(t), согласно формуле Q(t)=

находим:

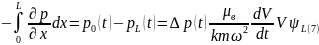
Где 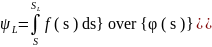(8)

Заметим, что, в отличие от (4), 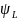, не постоянна, а зависит от времени, поскольку насыщенность на выходе из пласта s_L= s_L(t). Поэтому

уравнение (7) нельзя сразу проинтегрировать, разделив переменные, как это было сделано раньше.

Чтобы обойти эту трудность, сделаем замену переменных, перейдя в (8) от s к новой переменной F:

F = f’(s),

так что f’'(s)ds = dF, 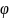(s) = 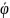(F), F = 0 при s = s’; F = f'(s_L) = F_L (t) при s = s_L.

Тогда (8) принимает вид

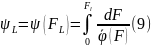
Из равенства

f’( ,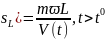

находим

V(t)=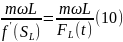

тогда

V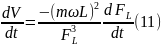

Подставив (9) и (11) в уравнение (7), получим:

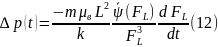
Полученное уравнение интегрируется при начальном условии

F_l=F_c=f'(s_c) при t=t°, которое следует из

V(t°)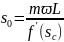

.В результате интег­рирования получим зависимость 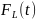в неявном виде:

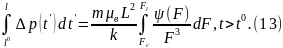
По зависимости F_L{t) можно рассчитать все необходимые показате­ли процесса вытеснения во второй стадии. Объем закачанной в пласт воды находится из (10), а из (12) и (9) получаем расчетную форму­лу суммарного дебита галереи:

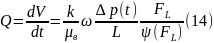
Расчеты по формулам (6) и (13) не вызывают принципиаль­ных затруднений и связаны только с численным или графическим выпол-

t

нением квадратур (4), (9) и вычислением интеграла