2.3 Розрахунок і конструювання другорядної балки

Розрахунок виконуємо у два етапи: спочатку статичний за методом граничної рівноваги, а потім – конструктивний.

2.3.1 Розрахункова схема балки

За розрахункову схему балки беремо п’ятипрольотну нерозрізну балку (рис. 2.6), опорами якої є головні балки.

Рисунок 2.6 – Розрахункова схема другорядної балки

Розміри прольотів балки призначаємо відповідно до п. 1.3.1. Для використаних у п. 2.2.2 розмірів перерізу h_sb = 450 мм, b_sb = 200 мм призначаємо довжину площадки обпирання балки на стіну В = 250 мм (рис.2.7).

Розміри перерізу головної балки призначаємо зі співвідношення

мм, приймаємо мм;

мм.

Довжину розрахункових прольотів балки (рис. 2.6) обчислюємо за формулами (1.27) – (1.28)

мм;

мм.

Інтенсивність прикладеного до балки рівномірно розподіленого навантаження (табл. 2.1) за (1.26)

кН/м.

2.3.2 Статичний розрахунок балки

Розрахунковими перерізами балки при розрахунку її міцності за методом граничної рівноваги будуть 1-1, 2-2, 3-3, 4-4 (рис. 2.6). Згинальні моменти, що діють в цих перерізах, визначаємо за (1.29) – (1.31).

Переріз 1-1

кНм.

Переріз 2-2

кНм.

Переріз 3-3

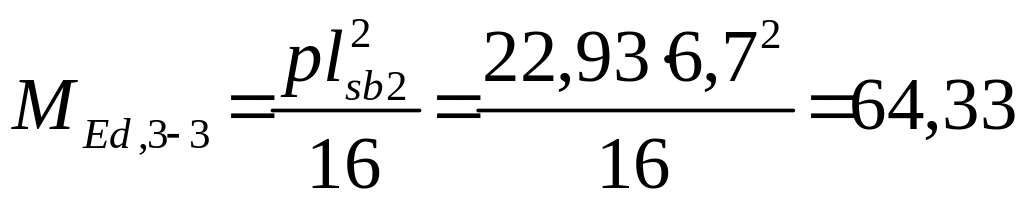кНм.

Переріз 4-4

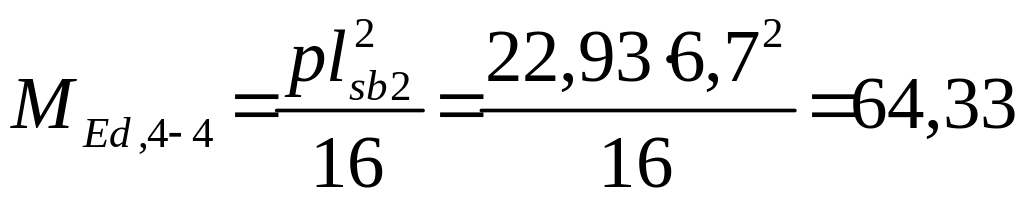кНм.

Максимальні поперечні сили, що діють на опорах, визначаємо за (1.33) – (1.35).

На крайній вільній опорі А

кН.

На першій проміжній опорі В зліва

кН.

На першій проміжній опорі В справа і на решті опор

кН.

2.3.3 Уточнення розмірів поперечного перерізу балки

Прийняті в п. 2.2.2 розміри поперечного перерізу балки необхідно уточнити, взявши за основу дані статичного розрахунку. При цьому керуємося п. 1.3.3, згідно з яким знаходимо робочу висоту балки в перерізі 2-2, оскільки тут діє максимальний згинальний момент.

У цьому перерізі плита монолітно зв’язана з балкою, участі в сприйнятті моменту не бере, оскільки вона перебуває в розтягнутій зоні.

Отже,

.

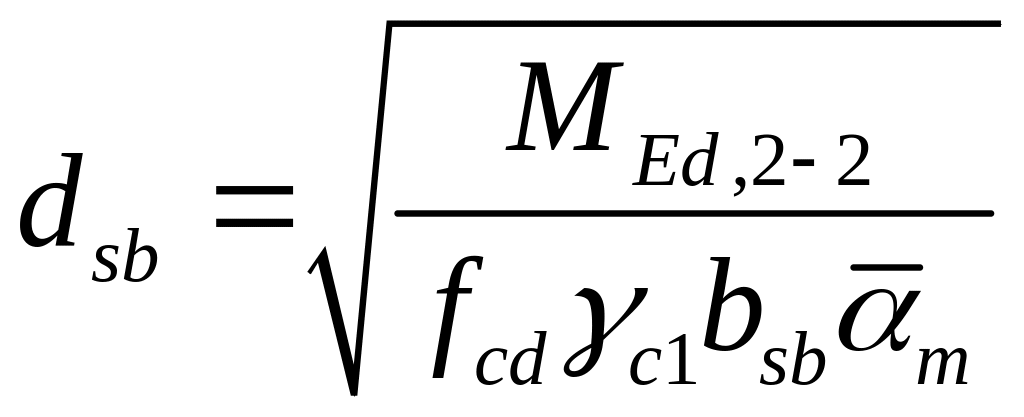У цьому виразі невідомим є коефіцієнт . Знайдемо його, задавшись коефіцієнтом армування балки і перевіривши, відповідає це значення умовам оптимального армування балки чи ні, а саме: чи дотримується умова . Згідно з (1.37), взявши значення ω = 0,792 з табл. А3, визначаємо

.

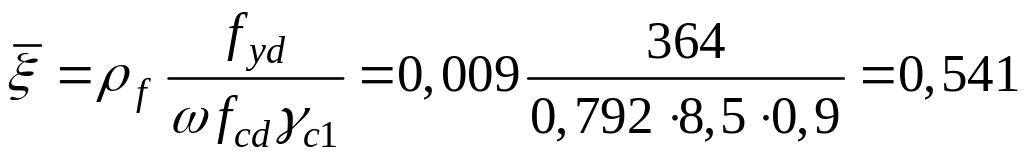За табл. А4 знайдемо, що .

Отримане значення , тобто умова (1.37) виконується. Отже, відсоток армування перебуває в межах його оптимальних значень.

Із табл. А5 для знаходимо:

;

.

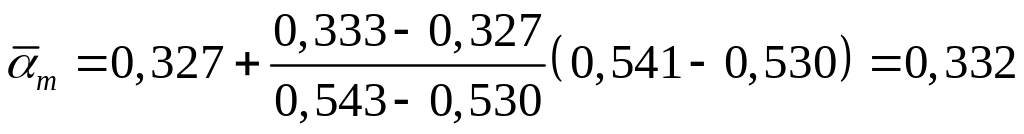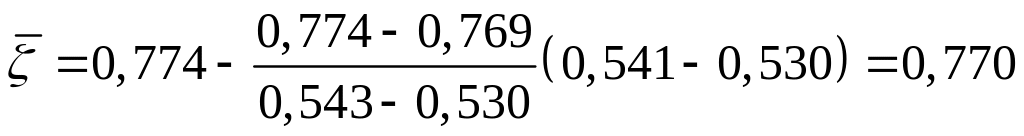Використовуючи обчислені значення коефіцієнтів отримуємо:

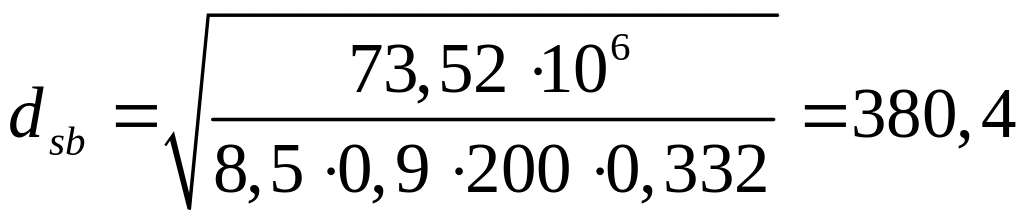мм.

Необхідна площа поздовжньої робочої арматури в перерізі 2-2 за (1.38)

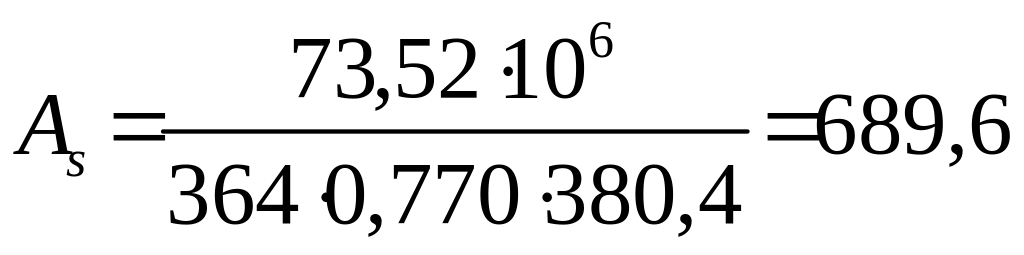мм².

Із табл. А6 видно, що поздовжню робочу арматуру попередньо можна прийняти у вигляді 210 + 220. Фактична площа вибраних стержнів мм².

Стержні 10 будуть також використані як конструктивна арматура.

Оскільки згідно з конструктивними вимогами для стержнів 20 в балках товщина захисного шару c_nom = 20 мм, то

мм.

Округливши отримане значення h_sb до кратного 50 мм у більший бік, матимемо, що h_sb = 450 мм. Звідси уточнюємо

мм.

Оскільки уточнена висота другорядної балки не відрізняється від попередньо прийнятої в п. 2.2.2 та п. 2.3.1, то перерахунок навантаження на балку виконувати не потрібно.