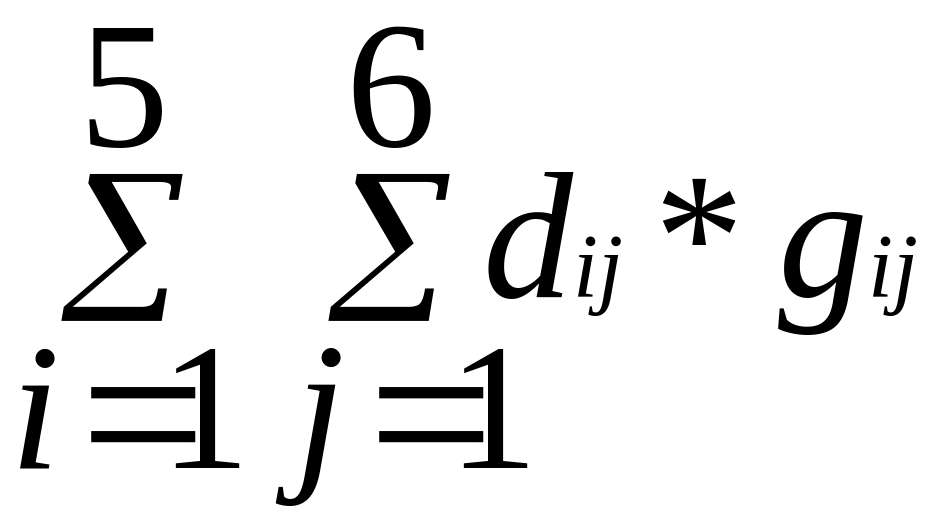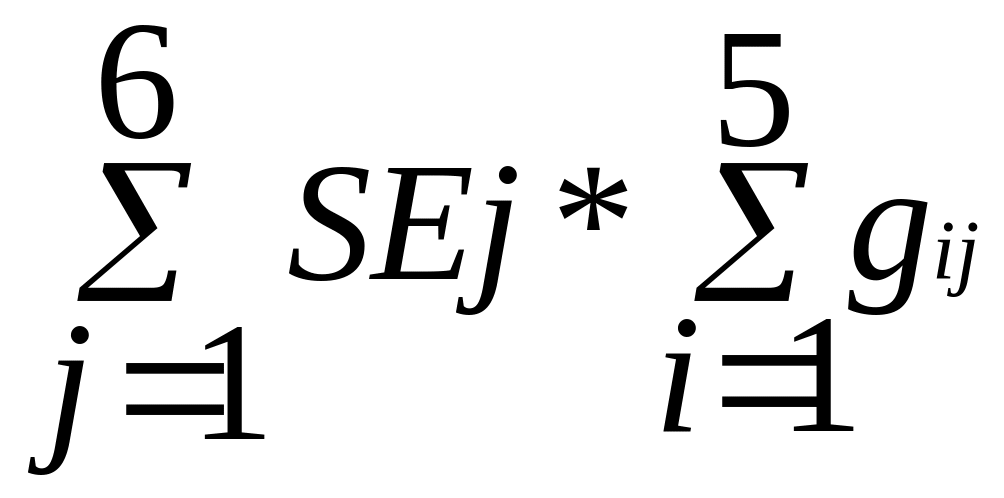Формализация рассматриваемой модели.

У рассматриваемой нами компании по производству и реализации картонных коробок в долгосрочной перспективе имеется два предложения по реконструкции ее производства в соответствии с прогнозируемым ростом спроса в средне-сибирском регионе. Первое из них касается значительного расширения завода в Перми, а второе – строительства нового завода в Иркутске.

Альтернативы:

1. Сохранить существующий порядок производства и реализации продукции компании.

2. Провести расширение и модернизацию завода в Перми.

3. Построить новый завод в Иркутске.

4. Провести расширение и модернизацию завода в Перми с одновременным строительством нового завода в Иркутске.

Для анализа данных альтернатив мы должны построить модель инвестиционных решений, связывающую затраты по производству, транспортировке и реализации продукции с необходимыми инвестициями.

Производство

В компании в настоящее время имеется 4 завода. При этом обсуждается возможность модернизации одного из них и/или строительства пятого. Ниже приводится характеристики заводов:

1. Вологодский завод. Наиболее старый завод компании с устаревшим оборудованием. Характеризуется низкой производительностью и высокими производственными затратами. Условно-переменные расходы составляют 448,3 долл. на тонну продукции. Производственная мощность - 14000 тонны в смену.

2. Псковский завод. Завод характеризуется наиболее низкими расходами на труд. Условно-переменные расходы составляют 416,9 долл. на тонну продукции. Производственная мощность - 12000 тонн в смену.

3. Пермский завод. Завод характеризуется высокими расходами на труд, хотя условно-переменные расходы низкие и составляют 408,5 долл. на тонну продукции. Производственная мощность - 16000 тонн в смену. Если завод будет подвергнут раширению и реконструкции, это потребует затрат в 3,1 млн.долл., но повысит его прозводственную мощность до 28000 тонн в смену.

4. Владивостокский завод. Самый новый из заводов компании. Условно-переменные расходы составляют 397,7 долл. на тонну продукции. Производственная мощность – 12000 тонн в смену.

5. Иркутский завод. Существует только пока в проекте. Его строительство составит 4 млн. долл. при производственной мощности в 12000 тонн в смену.

Распределение.

Компания имеет 6 региональных центров оптовой торговли (РЦОТ), через которые проводятся все торговые операции. Ниже приводятся их перечень с указанием объемов продаж за прошлый год ( для каждого варианта будут свои объемы продаж, см. табл. 1).

Калининградский РЦОТ	2 600 т
Новгородский РЦОТ	9 700 т
Новосибирский РЦОТ	15 500 т
Екатеринбурский РЦОТ	10 100 т
Иркутский РЦОТ	13 400 т
Хабаровский РЦОТ	7 500 т

Формализация проблемы

Решив задачу мы хотим определить, сколько продукции должно быть произведено на заводах компании и где произведенная продукция должна быть реализована, чтобы суммарные производственные и транспортные затраты были минимальны, а прибыль максимальна.

Переменные.

i	индекс завода ( i = 1, 2, 3, 4, 5 )
j	индекс РЦОП ( j = 1, 2, 3, 4, 5, 6 )
k	индекс номера смены k = 1, 2
xBkiB	объем производства первой и второй смены заводов в Вологде, Пскове, Перми, Владивостоке и Иркутске соотвественно.
gBijB	объемы перевозок от i - пункта производства к j - пункту потребления.
YBkiB	бинарная переменная ( принимающая только два значения – 0 или 1), показывающая, организуется ли данная смена в данном пункте производства или нет.
	Примечание: Значение бинарных переменных определяет, включаются ли условно-переменные расходы данной смены в рассмотрение или нет. Поскольку первые смены всегда имеют место на всех заводах компании, переменные YB11B, YB12B, YB13B,YB14B,YB15B фактически не выступают в модели в качестве управляемых, так как YB11B= YB12B =YB13 B=YB14B=YB15B = 1

Прочие переменные.

dBijB	расходы на транспортировку 1 т. продукции с завода i на РЦОТ j
CBiB	производственные мощности каждого из пяти заводов компании (в расчете на одну смену).
FCBkiB	условно-постоянные расходы каждой из двух смен на каждом из заводов компании
VBkiB	условно-переменные расходы на производство 1 т. продукции в каждую из двух смен на каждом из заводов компании.
SEBjB	затраты по реализации 1 т. продукции на каждом из РЦОТ.
DBjB	спрос на продукцию компании в каждом из обслуживаемых регионов (внешняя переменная).
	рыночная депозитная процентная ставка
KB1B	дополнительные инвестиции на покупку земли для строительства нового завода.
KB2B	дополнительные инвестиции на строительство нового завода
KB3B	дополнительные инвестиции на приобретение нового оборудования.

Целевая функция.

Целевая функция задачи должна выражать требование максимизации прибыли, которая определяется соотношением:

Прибыль = Объем реализации – производственные расходы –Транспортные расходы- затраты по реализации –затраты, связанные с инвестированием.			Ф.1
Запишем выражения для каждой из составляющих формулы Ф.1 в следующем виде:
Объем реализации = Цена *Продажи = Цена *
Производственные расходы =
Транспортные расходы =
Затраты по реализации =
Затраты, связанные с инвестированием = (KB1B+KB2B+KB3B)
UИтак, мы имеем выражение для целевой функции: Прибыль = Цена * - ( ) - -( )-(KB1B+KB2B+KB3B)

Ограничения

1. Объем перевозок продукции в каждый из регионов потребления должен быть равен имеющемуся в них спросу, т.е.

Для каждого j

2. Объем производства каждой смены на каждом из заводов компании не должен превышать односменной производственной мощности завода.

xB_12B,xB_21B<=CB_1B

xB_12B,xB_22B<=CB_2B

xB_13B,xB_23B<=CB_3B

xB_14B,xB_24B<=CB_4B

xB_15B,xB_25B<=CB_5B

3. Объем поставок, отправленных с каждого из заводов, должен быть равен ( не должен превышать) их двусменного объема производства:

4. Введем ограничения на бинарные переменные YB_{ki :B}

0<=YB_kiB<=1, YB_kiB – целочисленная.

В исходном случае функционирования четырех заводов будем полагать, что:

YB_{11 B}= YB_{12 B}= YB_{13 B}= YB_{14 B}=1

Ограничения связи.

Если мы используем вторую смену на каком-либо заводе, то имеют место следующие неравенства:

xB_21B-14000*YB_21B<=0

xB_22B-12000*YB_22B<=0

xB_23B-12000*YB_23B<=0

xB_24B-28000*YB_24B<=0

xB_25B-12000*YB_25B<=0

Чтобы при введении второй смены быть уверенным, что первая смена используется, введем следующие ограничения:

YB_21B – YB_11B <= 0

YB_22B – YB_12B <= 0

YB_23B – YB_13B <= 0

YB_24B – YB_14B <= 0

YB_25B – YB_15B <= 0

Ограничения,

связанные, с не отрицательностью искомых параметров.

Производимые объемы продукции и объемы перевозок не могут быть отрицательными числами.

xB_kiB >= 0

gB_ijB >=0.

Допущения:

• Величины оценивающие спрос, являются внешними переменными модели. Искомое оптимальное решение будет основываться на данных, оценивающих спрос за прошлый год.

• Будем полагать, что объем производства на каждом из заводов должен точно соответствовать спросу. Запасы недопустимы.

• Период амортизации земли и зданий каждого из заводов будем полагать равным 30 годам. амортизационный период для оборудования – 10 лет. При увеличении амортизационного периода соответствующие условно-постоянные расходы будут уменьшаться, а при уменьшении – увеличиваться.

• Будем считать, что условно-постоянные расходы первой смены имеют место всегда при условии, что данный завод работает. Условно-постоянные расходы второй смены вводятся в рассмотрение, только если производственных мощностей первой смены недостаточно для удовлетворения спроса.