Диференціальне обчислення функції однієї змінної Програма

Похідна функції, таблиця похідних. Похідна складної функції. Геометричний зміст похідної. Фізичний зміст похідної. Дослідження функції та побудова її графіка за допомогою похідної.

Зміст уміння для даної спеціальності: Використовувати математичні методи при розрахунках економічної ефективності технологічних процесів виготовлення типових зварних конструкцій. Визначати тип зварної конструкції, призначення її основних елементів; виконувати розрахунки нескладних елементів зварних конструкцій на міцність та визначати розміри їх перерізів при статичному навантаженні. Розраховувати та вибирати параметри режиму зварювання тиском. Розраховувати та вибирати параметри режиму зварювання плавленням.

Методичні вказівки

1. Вивчити навчальний матеріал за підручником В. Т. Лисичкин, И. Л. Соловейчик "Математика" розділ ІV, чи за будь-яким іншим підручником з поданих у списку літератури.

2. Ознайомитися з методичними вказівками до даної теми та розібрати розв’язання прикладів з даного посібника.

3. Дати відповіді на питання та виконати вправи для самоперевірки.

Границя функції в точці

Число в називають границею функції в точці х₀, якщо для всіх значень х, достатньо близьких до х₀ та нерівних х₀, значення функції мало відрізняються від числа х₀, записують: .

Приростом аргументу називається різниця між х₀ та х, де х – значення взяте з околу х₀: . Приріст функції , але , тоді .

Похідною функції в точці х₀ називається границя відношення приросту функції до приросту аргументу при , тобто .

Формули диференціювання:

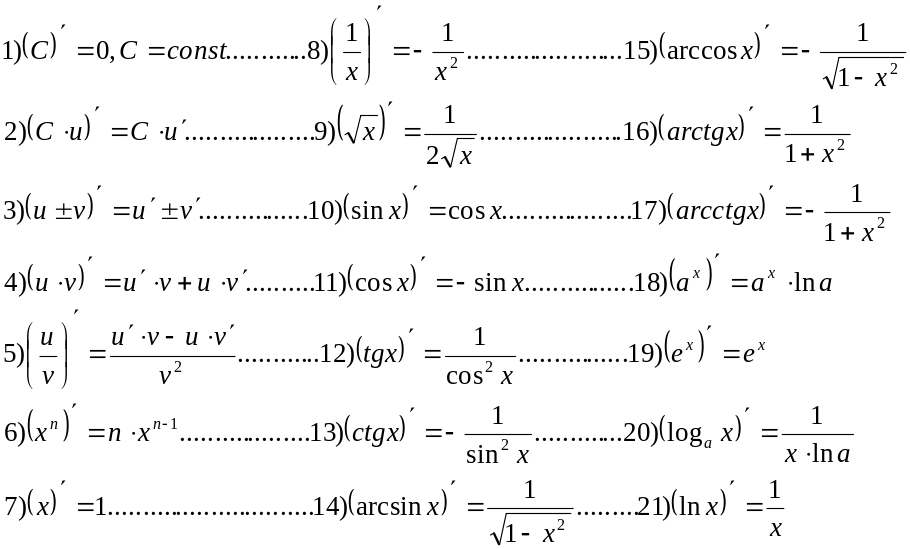
Приклад № 1. Знайти похідну даної функції

_{Розв’язання:}

Приклад № 2. Знайти похідну даної функції

_{Розв’язання:}

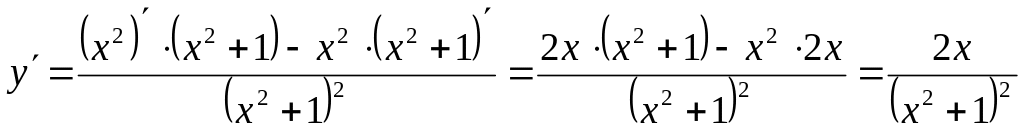
Похідна складної функції.

Теорема. Якщо функція f(и) має похідну по и, а и(х) має похідну по х, тоді похідна складної функції у=f(и(х)) по х визначається рівністю:

Приклад № 3. Знайти похідну даної функції

_{Розв’язання:}

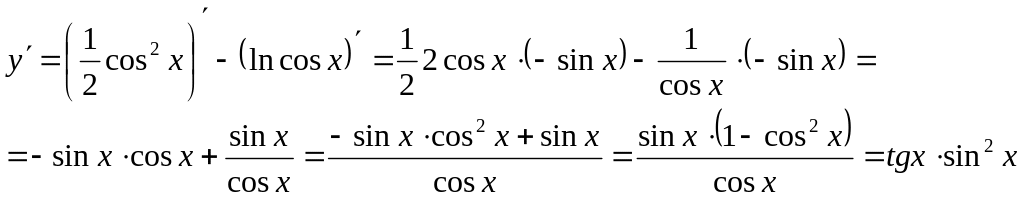
Геометричний зміст похідної. Рівняння дотичної.

Геометрична інтерпретація похідної (сформульована Лейбніцем в кінці XVII ст.): значення похідної функції у=f(x) в точці х_о дорівнює кутовому коефіцієнту дотичної, проведеної до графіку функції в точці х_о, тобто k=fⁱ(x_o)=tg .

З курсу шкільної геометрії, рівняння прямої з кутовим коефіцієнтом k,

що проходить через точку М_о(х_о,у_о) має вигляд: у – у_о = k( х – х_о).

Так як у_о=f(x_o) та k=fⁱ(x_o), тоді отримаємо рівняння дотичної до кривої у=f(x) в точці М(х_о,f(x_o)) :

Приклад № 4.

Скласти рівняння дотичної, проведеної до графіка функції _{в точці А(3;6).}

_{Розв’язання:}

Рівняння дотичної:

_{Знайдемо поступово коефіцієнти:}

1. 

2. 

3. 

Тоді рівняння дотичної матиме вигляд:

_{Відповідь:}

Фізичний зміст похідної: похідна показує швидкість зміни фізичної величини: .

Похідні вищих порядків.

Похідною другого порядку (другою похідною) функції у=f(x) називається похідна від її похідної, тобто .

Аналогічно, похідна третього порядку функції у=f(x) є похідна від її похідної другого порядку, тобто .

Взагалі, похідною п-го порядку від функції у=f(x) називається похідна від її похідної (п – 1) порядку, тобто .

Механічний зміст другої похідної: Якщо заданий закон прямолінійного руху точки, тоді друга похідна шляху за часом є прискоренням даного руху:

Приклад № 5. Закон руху тіла масою 2кг заданий формулою _{. Знайти силу, що примушує рухатися тіло протягом 1с.}

_{Розв’язання: За ІІ законом Ньютона , тоді}

_Отже,

_{Відповідь: 48Н.}