7.6. Случаи а ±1, а ± 2, а ± 3

1. У детей на партах разложены вырезанные из приложения сказочные цифры. Предлагается придумать из них чис­ловой ряд. На доске нарисована лента с оборванными краями. На ней изображена прямая с указанным направ­лением (например, вправо) и отмеченными четырьмя шагами (ограниченными пятью точками).

Учитель берет один знак и ставит его к средней точке на числовой прямой:

У. Какое это число?

Д. Наверное, это 3!

У. Неизвестно, ведь начало числовой прямой оказалось от­резанным. Теперь выберем знак для числа на 1 больше. С ка­кой стороны его поставить?

Д. Справа.

Вызванный ученик выбирает карточку с цифрой, учитель соглашается, подчеркивая произвольность выбора: «Пусть бу­дет такая цифра». Таким же образом дети самостоятельно вы­бирают знаки для остальных чисел.

Допустим, получился ряд: ╧ γ 0 γ n. Предлагается ука­зать самое маленькое из этих чисел; число больше его на 1; число меньше первого на 1 (его в ряду нет, а вообще-то оно су­ществует); число на 1 больше и на 1 меньше числа γ и т. п.

2. На доске записаны сказочные числовые выражения с цифрами из созданного числового ряда: γ+1, γ-1,

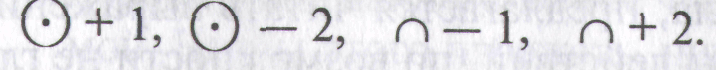
Учитель «замечает», что в этой сказочной школе «один» и «два» пишутся как обычно. Предлагается догадаться, какие числа получили сказочные ученики в результате заданных дей­ствий. Учитель указывает выражение, приписывает знак ра­венства, дети поднимают карточку с нужной цифрой — отве­том.

В последнем случае дать ответ нельзя из-за нехватки цифр.

2.Учебник, ч. 3, с. 3. Упр. 1. В учебнике сказочные цифры стоят в иной последовательности: этот порядок придума­ли другие дети. Уточняется, что первая цифра не означа­ет числа 1. Выясняется, какое из заданных чисел самое большое, а какое самое маленькое.

Дописываются заданные равенства. В объяснениях исполь­зуются понятия следующего и предыдущего чисел.

3.У учителя лист бумаги, сложенный гармошкой, на каж­дой грани которой написаны равенства вида а ± 1 = с и а ± 2 = с (с обычными цифрами). Учитель загораживает карточкой часть записи, закрывая второе число. Если спрятано число 1, дети должны поднять один палец. За­тем учитель снимает карточку, и все проверяют свое ре­шение. Рассуждение: если в равенстве записаны сосед­ние числа, значит, произошло увеличение или уменьше­ние на 1.

Учитель «восхищен» — дети работали «держа числовую пря­мую в уме».

Примечание. Мысленное движение по числовой прямой на один шаг, вероятно, уже освоено учащимися. На данном этапе обучения требуется связать направление движения со знаками «+» и «—» и соответствующими терминами.

4. Учебник, ч. 3, с. 3. Упр. 2. Просматривается первый стол­бик выражений. Отмечается последовательное измене­ние исходного числа, предлагается читать выражения и называть результаты действий, по возможности не глядя на числовую прямую. Под диктовку учеников учитель за­писывает соответствующие равенства на доске.

Обнаруживается, что столбик можно продолжить. Записы­ваются случаи до 9+1. Обращается внимание на постепенное увеличение числа, записанного после знака равенства.

Такая же работа проделывается со вторым столбиком. Учи­тель сообщает, что нужно тренироваться, чтобы научиться бы­стро и правильно производить такие действия «в уме». В каче­стве тренировки выполняется упр. 3 (учебник, ч. 3, с. 3).

Примечание. Начиная со с. 42 учебника даны упражне­ния, формирующие навык сложения и вычитания в преде­лах 10. Упражнения выполняются параллельно изучению но­вого учебного материала.

5. Учебник, ч. 3, с. 4. Упр. 4 Работа выполняется в парах: один ученик решает (с помощью жестов на числовой пря­мой) верхний пример, а другой — нижий. Затем выясня­ется, почему у обоих получился один и тот же результат.

6.Учебник, ч. 3, с. 4. Упр. 5. В сказочной школе тоже выполняли такие задания, один ученик решил верхний пример и нашел на сказочном числовом ряду указан­ное число. Какое число получит другой ученик? Выяс­няется, что оба должны проделать на числовой прямой одну и ту же работу, поэтому результат получится тот же. В последнем столбике скрыта «ловушка». Нельзя поста­вить во вторую запись то же число, что получено в пер­вой.

7. Учебник, ч. 3, с. 4. Упр. 6. Предлагается потренироваться в мысленной работе на числовой прямой. Не стоит при­учать детей к развернутой речевой формулировке спосо­ба действия, например: 5 + 1 — это 6,6+1 — это 7, зна­чит, 5 + 2 = 7. Это замедляет процесс присчитывания. Нужно, чтобы дети, увидев или услышав выражение, сразу называли следующие точки числовой прямой. Дети порой принимают исходное число за первый шаг по пря­мой. Чтобы этого избежать, нужно предложить детям не повторять заданное число — ведь его «уже слышали (ви­дели в записи)». Поэтому работу с упр. 7 можно органи­зовать так.

Один ученик вслух читает исходное число, а остальные дети последовательно хором произносят следующие или предыду­щие числа. При этом они должны по виду знака быстро опре­делить направление движения по числовому ряду, досчитать до нужного числа и вовремя остановиться.

8.Учебник, ч. 3, с. 4. Упр. 7. По рисунку требуется соста­вить рассказ-задачу и решить ее, т. е. найти ответ и записать соответствующее равенство. Само движение по числовой прямой детям предлагается выполнить мыс­ленно. Не нужно требовать от детей отчета о том, что та­кое задача, что такое решение, просто учитель начинает активно использовать эти термины. Упражнения в со­ставлении и решении задач представлены на следующих двух страницах учебника. (Параллельно выполняются задания на отработку случаев прибавления и вычитания чисел 1 и 2.)

9. Учебник, ч. 3, с. 5, 6. Упр. 1 — 6. Материал для составле­ния и решения задач прорабатывается параллельно рабо­те со с. 7 — 12 учебника.